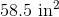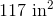Geometry
Help Questions
6th Grade Math › Geometry
Select the graph that displays the polygon created using the following coordinates:




Explanation
When we are given coordinate points, it's important to know the difference between the x-axis and the y-axis, and which order these points are given. The x-axis is the axis that runs left to right and the y-axis is the axis the runs up and down. When coordinate points are written, the x value goes first, followed by the y value 
Knowing this information, we can plot the points and use straight lines to connect them in a counter-clockwise or clockwise direction. The provided coordinate points should create the following graph:

A large crate in the shape of a rectangular prism has dimensions 5 feet by 4 feet by 12 feet. Give its volume in cubic yards.
Explanation
Divide each dimension by 3 to convert feet to yards, then multiply the three dimensions together:
What is the area of the right triangle in the following figure?

Explanation
There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

What is the area of the right triangle in the following figure?

Explanation
There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Select the graph that displays the polygon created using the following coordinates:




Explanation
When we are given coordinate points, it's important to know the difference between the x-axis and the y-axis, and which order these points are given. The x-axis is the axis that runs left to right and the y-axis is the axis the runs up and down. When coordinate points are written, the x value goes first, followed by the y value 
Knowing this information, we can plot the points and use straight lines to connect them in a counter-clockwise or clockwise direction. The provided coordinate points should create the following graph:

Select the graph that displays the polygon created using the following coordinates:




Explanation
When we are given coordinate points, it's important to know the difference between the x-axis and the y-axis, and which order these points are given. The x-axis is the axis that runs left to right and the y-axis is the axis the runs up and down. When coordinate points are written, the x value goes first, followed by the y value 
Knowing this information, we can plot the points and use straight lines to connect them in a counter-clockwise or clockwise direction. The provided coordinate points should create the following graph:

Select the graph that displays the polygon created using the following coordinates:




Explanation
When we are given coordinate points, it's important to know the difference between the x-axis and the y-axis, and which order these points are given. The x-axis is the axis that runs left to right and the y-axis is the axis the runs up and down. When coordinate points are written, the x value goes first, followed by the y value 
Knowing this information, we can plot the points and use straight lines to connect them in a counter-clockwise or clockwise direction. The provided coordinate points should create the following graph:

Select the graph that displays the polygon created using the following coordinates:




Explanation
When we are given coordinate points, it's important to know the difference between the x-axis and the y-axis, and which order these points are given. The x-axis is the axis that runs left to right and the y-axis is the axis the runs up and down. When coordinate points are written, the x value goes first, followed by the y value 
Knowing this information, we can plot the points and use straight lines to connect them in a counter-clockwise or clockwise direction. The provided coordinate points should create the following graph:

What is the area of the right triangle in the following figure?

Explanation
There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Hydraulic fracturing is a process used by gas companies to rupture and collects pockets of gas trapped within pockets of shale rock. A particular shale fracking site is 

Explanation
In order to solve this question, we need to first recall how to find the area of a rectangle.
Substitute in the given values in the equation and solve for 
Divide both sides by
Dividing by a fraction is the same as multiplying by its inverse or reciprocal.
Find the reciprocal of
Simplify and rewrite.
Multiply and solve.
Reduce.
The width of the fracking site is