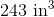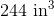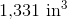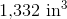Geometry
Help Questions
7th Grade Math › Geometry
Calculate the volume of the provided figure.

Explanation
In order to solve this problem, we need to recall the volume formula for a rectangular prism:
Now that we have the correct formula, we can substitute in our known values and solve:

The above diagram shows a rectangular solid. The shaded side is a square. In terms of 
Explanation
A square has four sides of equal length, as seen in the diagram below.

The volume of the solid is equal to the product of its length, width, and height, as follows:

The length of the side of a cube is 

Explanation
Substitute 
If a cube has one side measuring 
Explanation
To find the surface area of a cube, use the formula 




What angle is complement to 
Explanation
The complement to an angle is ninety degrees subtract the angle since two angles must add up to 90. In this case, since we are given the angle in radians, we are subtracting from 
Reconvert the fractions to the least common denominator.
Reduce the fraction.

What is the area of the triangle pictured above?
12
24
30
40
60
Explanation
The area of a triangle is calculated using the formula 

Calculate the volume of the provided figure.

Explanation
In order to solve this problem, we need to recall the volume formula for a cube:
Now that we have the correct formula, we can substitute in our known values and solve:
Calculate the area of the provided figure.

Explanation
In order to solve this problem, we need to recall the area formula for a circle:
Now that we have the correct formula, we can substitute in our known values and solve:
Find the surface area of a non-cubic prism with the following measurements:
Explanation
The surface area of a non-cubic prism can be determined using the equation:
Calculate the area of the provided figure.

Explanation
In order to solve this problem, we need to recall the area formula for a triangle:
Now that we have the correct formula, we can substitute in our known values and solve: