Expressions - ACT Math
Card 0 of 981
If  , what is the value of:
, what is the value of:

If 
Substituting x+y for 5, we get
6(5) - 52 + (1/5)(5) + 8
30 - 25 + 1 + 8
= 14
Substituting x+y for 5, we get
6(5) - 52 + (1/5)(5) + 8
30 - 25 + 1 + 8
= 14
Compare your answer with the correct one above
Evaluate 4x2 + 6x – 17, when x = 3.
Evaluate 4x2 + 6x – 17, when x = 3.
Plug in 3 for x, giving you 36 + 18 – 17, which equals 37.
Plug in 3 for x, giving you 36 + 18 – 17, which equals 37.
Compare your answer with the correct one above
John has a motorcycle. He drives it to the store, which is 30 miles away. It takes him 30 minutes to drive there and 60 minutes to drive back, due to traffic. What was his average speed roundtrip in miles per hour?
John has a motorcycle. He drives it to the store, which is 30 miles away. It takes him 30 minutes to drive there and 60 minutes to drive back, due to traffic. What was his average speed roundtrip in miles per hour?
The whole trip is 60 miles, and it takes 90 minutes, which is 1.5 hours.
Miles per hour is 60/1.5 = 40 mph
The whole trip is 60 miles, and it takes 90 minutes, which is 1.5 hours.
Miles per hour is 60/1.5 = 40 mph
Compare your answer with the correct one above
If (xy/2) – 3_w_ = –9, what is the value of w in terms of x and y?
If (xy/2) – 3_w_ = –9, what is the value of w in terms of x and y?
–3_w_ = –9 – (xy/2)
w = 3 + (xy/6)
–3_w_ = –9 – (xy/2)
w = 3 + (xy/6)
Compare your answer with the correct one above
Evaluate 5_x_2 + 16_x_ + 7 when x = 7
Evaluate 5_x_2 + 16_x_ + 7 when x = 7
Plug in 7 for x and you get 5(49) + 16(7) + 7 = 364
Plug in 7 for x and you get 5(49) + 16(7) + 7 = 364
Compare your answer with the correct one above
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Compare your answer with the correct one above
What is  ?
?
What is 
 factors to
factors to  . Thus,
. Thus,  . Canceling out like terms leads to
. Canceling out like terms leads to  .
.




Compare your answer with the correct one above
Simplify the following rational expression:

Simplify the following rational expression:
Since both fractions in the expression have a common denominator of  , we can combine like terms into a single numerator over the denominator:
, we can combine like terms into a single numerator over the denominator:



Since both fractions in the expression have a common denominator of 
Compare your answer with the correct one above
Simplify the following rational expression:

Simplify the following rational expression:
Since both rational terms in the expression have the common denominator  , combine the numerators and simplify like terms:
, combine the numerators and simplify like terms:




Since both rational terms in the expression have the common denominator 
Compare your answer with the correct one above
Simplify the following expression:

Simplify the following expression:
Since both terms in the expression have the common denominator  , combine the fractions and simplify the numerators:
, combine the fractions and simplify the numerators:



Since both terms in the expression have the common denominator 
Compare your answer with the correct one above
Compute the following: 
Compute the following:
Notice that the denominator are the same for both terms. Since they are both the same, the fractions can be added. The denominator will not change in this problem.

Notice that the denominator are the same for both terms. Since they are both the same, the fractions can be added. The denominator will not change in this problem.
Compare your answer with the correct one above
A company rents cars for a rental fee of \$37.00 per day, with an additional charge of \$0.45 per mile driven. Which of the following expressions represents the cost, in dollars, of renting the car for 2 days and driving it m miles?
A company rents cars for a rental fee of \$37.00 per day, with an additional charge of \$0.45 per mile driven. Which of the following expressions represents the cost, in dollars, of renting the car for 2 days and driving it m miles?
To determine cost we add the initial rental fee of \$37, times two days giving us \$74 plus the mileage rate, 0.45, times the number of miles. Giving an equation of 0.45m+74.
To determine cost we add the initial rental fee of \$37, times two days giving us \$74 plus the mileage rate, 0.45, times the number of miles. Giving an equation of 0.45m+74.
Compare your answer with the correct one above
Combine the following rational expressions:

Combine the following rational expressions:
When working with complex fractions, it is important not to let them intimidate you. They follow the same rules as regular fractions!

In this case, our problem is made easier by the fact that we already have a common denominator. Nothing fancy is required to start. Simply add the numerators:

For our next step, we need to combine like terms. This is easier to see if we group them together.


Thus, our final answer is:

When working with complex fractions, it is important not to let them intimidate you. They follow the same rules as regular fractions!
In this case, our problem is made easier by the fact that we already have a common denominator. Nothing fancy is required to start. Simply add the numerators:
For our next step, we need to combine like terms. This is easier to see if we group them together.
Thus, our final answer is:
Compare your answer with the correct one above
Simplify the following expression:

Simplify the following expression:
In order to add fractions, we must first make sure they have the same denominator.
So, we multiply  by
by  and get the following:
and get the following:


Then, we add across the numerators and simplify:

In order to add fractions, we must first make sure they have the same denominator.
So, we multiply 

Then, we add across the numerators and simplify:
Compare your answer with the correct one above
Simplify the following:

Simplify the following:
To simplify the following, a common denominator must be achieved. In this case, the first term must be multiplied by (x+2) in both the numerator and denominator and likewise with the second term with (x-3).


To simplify the following, a common denominator must be achieved. In this case, the first term must be multiplied by (x+2) in both the numerator and denominator and likewise with the second term with (x-3).
Compare your answer with the correct one above
Simplify the following 
Simplify the following
Find the least common denominator between x-3 and x-4, which is (x-3)(x-4). Therefore, you have  . Multiplying the terms out equals
. Multiplying the terms out equals  . Combining like terms results in
. Combining like terms results in  .
.
Find the least common denominator between x-3 and x-4, which is (x-3)(x-4). Therefore, you have 


Compare your answer with the correct one above
Sally is ordering snacks for her class trip. She needs 85 cookies. The cookies come in cases of 6 boxes, with 7 cookies in each box. Sally can't order a partial box. What is the smallest number of cases she should order?
Sally is ordering snacks for her class trip. She needs 85 cookies. The cookies come in cases of 6 boxes, with 7 cookies in each box. Sally can't order a partial box. What is the smallest number of cases she should order?
We first determine how many cookies are in each box. There are 7 cookies in a box, multiplied by 6 boxes, making 42 cookies in a case. We then divide the total number of cookies she needs, 85, by the number in each case, 42, giving us 2 with a remainder. This means Sally must order 3 cases of cookies.
We first determine how many cookies are in each box. There are 7 cookies in a box, multiplied by 6 boxes, making 42 cookies in a case. We then divide the total number of cookies she needs, 85, by the number in each case, 42, giving us 2 with a remainder. This means Sally must order 3 cases of cookies.
Compare your answer with the correct one above
Select the expression that is equivalent to

Select the expression that is equivalent to
To add the two fractions, a common denominator must be found. With one-term denominators, it is easier to simply find the least common denominator between them and multiply each side to obtain it.
In this case, the least common denominator between  and
and  is
is  . So the first fraction needs to be multiplied by
. So the first fraction needs to be multiplied by  and the second by
and the second by  :
:


Now, we can add straight across, remembering to combine terms where we can.

So, our simplified answer is 
To add the two fractions, a common denominator must be found. With one-term denominators, it is easier to simply find the least common denominator between them and multiply each side to obtain it.
In this case, the least common denominator between 




Now, we can add straight across, remembering to combine terms where we can.
So, our simplified answer is
Compare your answer with the correct one above
Combine the following two expressions if possible.

Combine the following two expressions if possible.
For binomial expressions, it is often faster to simply FOIL them together to find a common trinomial than it is to look for individual least common denominators. Let's do that here:

FOIL and simplify.

Combine numerators.

Thus, our answer is 
For binomial expressions, it is often faster to simply FOIL them together to find a common trinomial than it is to look for individual least common denominators. Let's do that here:
FOIL and simplify.
Combine numerators.
Thus, our answer is
Compare your answer with the correct one above
Which of the following is equivalent to  ? Assume that denominators are always nonzero.
? Assume that denominators are always nonzero.
Which of the following is equivalent to 
We will need to simplify the expression  . We can think of this as a large fraction with a numerator of
. We can think of this as a large fraction with a numerator of  and a denominator of
and a denominator of  .
.
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator.  has a denominator of
has a denominator of  , and
, and 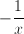 has a denominator of
has a denominator of  . The least common denominator that these two fractions have in common is
. The least common denominator that these two fractions have in common is  . Thus, we are going to write equivalent fractions with denominators of
. Thus, we are going to write equivalent fractions with denominators of 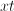 .
.
In order to convert the fraction  to a denominator with
to a denominator with 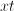 , we will need to multiply the top and bottom by
, we will need to multiply the top and bottom by  .
.

Similarly, we will multiply the top and bottom of  by
by  .
.

We can now rewrite  as follows:
as follows:
 =
= 
Let's go back to the original fraction  . We will now rewrite the numerator:
. We will now rewrite the numerator:
 =
= 
To simplify this further, we can think of  as the same as
as the same as  . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words,
. When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words,  .
.
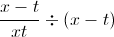 =
= 


Lastly, we will use the property of exponents which states that, in general,  .
.

The answer is  .
.
We will need to simplify the expression 


In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. 

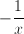


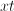
In order to convert the fraction 
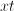

Similarly, we will multiply the top and bottom of 

We can now rewrite 

Let's go back to the original fraction 

To simplify this further, we can think of 


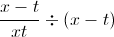
Lastly, we will use the property of exponents which states that, in general, 
The answer is 
Compare your answer with the correct one above