Quadratic Functions - Algebra 2
Card 1 of 592
Give the solution set of the inequality:

Give the solution set of the inequality:
Tap to reveal answer
Rewrite in standard form and factor:




The zeroes of the polynomial are therefore  , so we test one value in each of three intervals
, so we test one value in each of three intervals  ,
,  , and
, and  to determine which ones are included in the solution set.
to determine which ones are included in the solution set.
 :
:
Test  :
:



False;  is not in the solution set.
is not in the solution set.
 :
:
Test 


True;  is in the solution set
is in the solution set
 :
:
Test  :
:



False;  is not in the solution set.
is not in the solution set.
Since the inequality symbol is  , the boundary points are not included. The solution set is the interval
, the boundary points are not included. The solution set is the interval  .
.
Rewrite in standard form and factor:
The zeroes of the polynomial are therefore 




Test 
False; 

Test
True; 

Test 
False; 
Since the inequality symbol is 

← Didn't Know|Knew It →
Give the set of solutions for this inequality:

Give the set of solutions for this inequality:
Tap to reveal answer
The first step of questions like this is to get the quadratic in its standard form. So we move the  over to the left side of the inequality:
over to the left side of the inequality:

This quadratic can easily be factored as . So now we can write this in the form
. So now we can write this in the form

and look at each of the factors individually. Recall that a negative number times a negative is a positive number. Therefore the boundaries of our solution interval is going to be when both of these factors are negative.  is negative whenever
is negative whenever  , and
, and  is negative whenever
is negative whenever  . Since
. Since  , one of our boundaries will be
, one of our boundaries will be  . Remember that this will be an open interval since it is less than, not less than or equal to.
. Remember that this will be an open interval since it is less than, not less than or equal to.
Our other boundary will be the other point when the product of the factors becomes positive. Remember that  is positive when
is positive when  , so our other boundary is
, so our other boundary is  . So the solution interval we arrive at is
. So the solution interval we arrive at is

The first step of questions like this is to get the quadratic in its standard form. So we move the 
This quadratic can easily be factored as
and look at each of the factors individually. Recall that a negative number times a negative is a positive number. Therefore the boundaries of our solution interval is going to be when both of these factors are negative. 





Our other boundary will be the other point when the product of the factors becomes positive. Remember that 


← Didn't Know|Knew It →
Solve for 

Solve for
Tap to reveal answer
When asked to solve for x we need to isolate x on one side of the equation.
To do this our first step is to subtract 7 from both sides.


From here, we divide by 4 to solve for x.


When asked to solve for x we need to isolate x on one side of the equation.
To do this our first step is to subtract 7 from both sides.
From here, we divide by 4 to solve for x.
← Didn't Know|Knew It →
Solve for 

Solve for
Tap to reveal answer
When asked to solve for y we need to isolate the variable on one side and the constants on the other side.
To do this we first add 9 to both sides.


From here, we divide by -12 to solve for y.


When asked to solve for y we need to isolate the variable on one side and the constants on the other side.
To do this we first add 9 to both sides.
From here, we divide by -12 to solve for y.
← Didn't Know|Knew It →
The graphs of the lines  and
and  are shown on the figure. The region
are shown on the figure. The region  is defined by which two inequalities?
is defined by which two inequalities?

The graphs of the lines 



Tap to reveal answer
The region  contains only
contains only  values which are greater than or equal to those on the line
values which are greater than or equal to those on the line  , so its
, so its  values are
values are  .
.
Similarly, the region contains only  values which are less than or equal to those on the line
values which are less than or equal to those on the line  , so its
, so its  values are
values are  .
.
The region 




Similarly, the region contains only 



← Didn't Know|Knew It →
The graphs for the lines  and
and  are shown in the figure. The region
are shown in the figure. The region  is defined by which two inequalities?
is defined by which two inequalities?

The graphs for the lines 



Tap to reveal answer
The region  contains only
contains only  values which are greater than or equal to those on the line
values which are greater than or equal to those on the line  , so its
, so its  values are
values are  .
.
Also, the region contains only  values which are less than or equal to those on the line
values which are less than or equal to those on the line  , so its
, so its  values are
values are  .
.
The region 




Also, the region contains only 



← Didn't Know|Knew It →
Which of the following graphs correctly represents the quadratic inequality below (solutions to the inequalities are shaded in blue)?

Which of the following graphs correctly represents the quadratic inequality below (solutions to the inequalities are shaded in blue)?
Tap to reveal answer
To begin, we analyze the equation given: the base equation,  is shifted left one unit and vertically stretched by a factor of 2. The graph of the equation
is shifted left one unit and vertically stretched by a factor of 2. The graph of the equation  is:
is:

To solve the inequality, we need to take a test point and plug it in to see if it matches the inequality. The only points that cannot be used are those directly on our parabola, so let's use the origin  . If plugging this point in makes the inequality true, then we shade the area containing that point (in this case, outside the parabola); if it makes the inequality untrue, then the opposite side is shaded (in this case, the inside of the parabola). Plugging the numbers in shows:
. If plugging this point in makes the inequality true, then we shade the area containing that point (in this case, outside the parabola); if it makes the inequality untrue, then the opposite side is shaded (in this case, the inside of the parabola). Plugging the numbers in shows:

Simplified as:

Which is not true, so the area inside of the parabola should be shaded, resulting in the following graph:

To begin, we analyze the equation given: the base equation, 


To solve the inequality, we need to take a test point and plug it in to see if it matches the inequality. The only points that cannot be used are those directly on our parabola, so let's use the origin 
Simplified as:
Which is not true, so the area inside of the parabola should be shaded, resulting in the following graph:

← Didn't Know|Knew It →
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain  .
.
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
← Didn't Know|Knew It →
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain
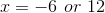
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
← Didn't Know|Knew It →
What is the greatest possible value of the  -coordinate?
-coordinate?

What is the greatest possible value of the 
Tap to reveal answer
This equation describes a circle of radius  (square root of
(square root of  ), centered at the point
), centered at the point  . The equation (which is NOT a function) has a maximum y-coordinate value directly above the center of the circle in the vertical direction. Take the y-coordinate of the center,
. The equation (which is NOT a function) has a maximum y-coordinate value directly above the center of the circle in the vertical direction. Take the y-coordinate of the center,  , and add to it the length of the radius,
, and add to it the length of the radius,  , to get the answer,
, to get the answer,  .
.
This equation describes a circle of radius 





← Didn't Know|Knew It →
Find the  intercept of a circle.
intercept of a circle.

Find the 
Tap to reveal answer

Let

Therefore the equation becomes,

Solve for x.









Let
Therefore the equation becomes,
Solve for x.
← Didn't Know|Knew It →
Find the  intercept of a circle.
intercept of a circle.

Find the 
Tap to reveal answer

Let

Therefore, the equation becomes:

Solve for y.








Let
Therefore, the equation becomes:
Solve for y.
← Didn't Know|Knew It →
A circle centered at  has a radius of
has a radius of  units.
units.
What is the equation of the circle?
A circle centered at 

What is the equation of the circle?
Tap to reveal answer
The equation for a circle centered at the point (h, k) with radius r units is
 .
.
Setting  ,
,  , and
, and  yields
yields

 .
.
The equation for a circle centered at the point (h, k) with radius r units is

Setting 



← Didn't Know|Knew It →
Convert the following angle to radians

Convert the following angle to radians
Tap to reveal answer
To convert degrees to radians, multiply degrees by:


Therefore 
To convert degrees to radians, multiply degrees by:
Therefore
← Didn't Know|Knew It →
Find the negative coterminal of 160.
Find the negative coterminal of 160.
Tap to reveal answer
Coterminal angles are angles that are the same but written differently. Circles have 360 degrees, so an angle that goes above this threshold has completed one revolution. For example, a 450 degree angle would be in the same position as a 90 degree angle.
To find a positive coterminal angle, add 360 degrees to the initial value.
To find the negative coterminal angle, simply subtract 360. The only exception to this rule would be if the initial value were greater than 360. In this case, subtract 360 until the value is negative, making it a negative coterminal. Therefore,
160-360 = -200
Do this a second time and we get -560. These are examples of negative coterminal angles.
Coterminal angles are angles that are the same but written differently. Circles have 360 degrees, so an angle that goes above this threshold has completed one revolution. For example, a 450 degree angle would be in the same position as a 90 degree angle.
To find a positive coterminal angle, add 360 degrees to the initial value.
To find the negative coterminal angle, simply subtract 360. The only exception to this rule would be if the initial value were greater than 360. In this case, subtract 360 until the value is negative, making it a negative coterminal. Therefore,
160-360 = -200
Do this a second time and we get -560. These are examples of negative coterminal angles.
← Didn't Know|Knew It →
Which of the following equations represent a circle?
Which of the following equations represent a circle?
Tap to reveal answer
The circle is represented by the formula:

Although some of the equations might not in this form, we can see by the variables that the equation  is most similar to the form.
is most similar to the form.
Multiply two on both sides of the equation and we will have:

This is an equation of a circle. The other equations represent other conic shapes.
The answer is: 
The circle is represented by the formula:
Although some of the equations might not in this form, we can see by the variables that the equation 
Multiply two on both sides of the equation and we will have:
This is an equation of a circle. The other equations represent other conic shapes.
The answer is:
← Didn't Know|Knew It →
Determine the equation of a circle that has radius  and is centered at
and is centered at 
Determine the equation of a circle that has radius 
Tap to reveal answer
Definition of the formula of a circle:

Where:
 is the
is the  coordinate of the center of the circle
coordinate of the center of the circle
 is the
is the  coordinate of the center of the circle
coordinate of the center of the circle
 is the radius of the circle
is the radius of the circle
Plugging in values:

Definition of the formula of a circle:
Where:





Plugging in values:
← Didn't Know|Knew It →
Determine the center and radius, respectively, given the equation:

Determine the center and radius, respectively, given the equation:
Tap to reveal answer
In order to solve for the radius, we will need to complete the square twice.
Group the x and y-variables in parentheses. Starting from the original equation:


Add two on both sides.

Divide by the second term coefficient of each binomial by 2, and add the squared quantity on both sides of the equation.

The equation becomes:

Factorize both polynomials in parentheses and simplify the right side.

The center is: 
The radius is: 
The answer is: 
In order to solve for the radius, we will need to complete the square twice.
Group the x and y-variables in parentheses. Starting from the original equation:
Add two on both sides.
Divide by the second term coefficient of each binomial by 2, and add the squared quantity on both sides of the equation.
The equation becomes:
Factorize both polynomials in parentheses and simplify the right side.
The center is:
The radius is:
The answer is:
← Didn't Know|Knew It →
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain  .
.
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
← Didn't Know|Knew It →
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain
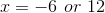
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
← Didn't Know|Knew It →