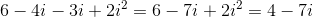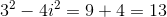Imaginary Numbers - Algebra 2
Card 1 of 676
Where would  fall on the number line?
fall on the number line? 
Where would 
Tap to reveal answer
Imaginary numbers do not fall on the number line-- they are by definition not real numbers.
** If the question asked where  falls on the number line, the answer would be to the left of 0, because
falls on the number line, the answer would be to the left of 0, because  .
.
Imaginary numbers do not fall on the number line-- they are by definition not real numbers.
** If the question asked where 

← Didn't Know|Knew It →
Solve for 

Solve for
Tap to reveal answer
Use the change of base formula for logarithmic functions and incorporate the fact that  and
and 

Or
 can be solved using
can be solved using 



Use the change of base formula for logarithmic functions and incorporate the fact that 
Or

← Didn't Know|Knew It →
Write the complex number  in polar form, where polar form expresses the result in terms of a distance from the origin
in polar form, where polar form expresses the result in terms of a distance from the origin  on the complex plane and an angle from the positive
on the complex plane and an angle from the positive  -axis,
-axis, 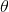 , measured in radians.
, measured in radians.
Write the complex number 


Tap to reveal answer
To see what the polar form of the number is, it helps to draw it on a graph, where the horizontal axis is the imaginary part and the vertical axis the real part. This is called the complex plane.

To find the angle  , we can find its supplementary angle
, we can find its supplementary angle  and subtract it from
and subtract it from  radians, so
radians, so  .
.
Using trigonometric ratios, 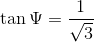 and
and  .
.
Then  .
.
To find the distance  , we need to find the distance from the origin to the point
, we need to find the distance from the origin to the point  . Using the Pythagorean Theorem to find the hypotenuse
. Using the Pythagorean Theorem to find the hypotenuse  ,
,  or
or  .
.
To see what the polar form of the number is, it helps to draw it on a graph, where the horizontal axis is the imaginary part and the vertical axis the real part. This is called the complex plane.

To find the angle 



Using trigonometric ratios, 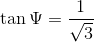

Then 
To find the distance 




← Didn't Know|Knew It →
Where does  fall on the number line?
fall on the number line?
Where does 
Tap to reveal answer
Imaginary numbers do not fall on the number line by definition, since they are not real numbers. However, although i is an imaginary number equal to the square root of -1,  is a real number since
is a real number since  . Therefore,
. Therefore,  . Negative numbers fall to the left of 0 on a number line.
. Negative numbers fall to the left of 0 on a number line.
Imaginary numbers do not fall on the number line by definition, since they are not real numbers. However, although i is an imaginary number equal to the square root of -1, 


← Didn't Know|Knew It →
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Tap to reveal answer
In complex numbers of the form  , a represents the real portion of the number and b represents the imaginary portion of the number. To graph
, a represents the real portion of the number and b represents the imaginary portion of the number. To graph  on a plane in which real numbers are represented by the x-axis and imaginary numbers are represented by the y-axis, place a point a units right of the origin and b units above the origin. The graph shows a point 2 units right and 3 units above the origin, so the complex number represented is
on a plane in which real numbers are represented by the x-axis and imaginary numbers are represented by the y-axis, place a point a units right of the origin and b units above the origin. The graph shows a point 2 units right and 3 units above the origin, so the complex number represented is  .
.
In complex numbers of the form 


← Didn't Know|Knew It →
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Tap to reveal answer
In complex numbers of the form  , a represents the real portion of the number and b represents the imaginary portion of the number. To graph
, a represents the real portion of the number and b represents the imaginary portion of the number. To graph  on a plane in which real numbers are represented by the x-axis and imaginary numbers are represented by the y-axis, place a point a units right of the origin and b units above the origin. The graph shows a point 5 units left and 2 units below the origin, so the complex number represented is
on a plane in which real numbers are represented by the x-axis and imaginary numbers are represented by the y-axis, place a point a units right of the origin and b units above the origin. The graph shows a point 5 units left and 2 units below the origin, so the complex number represented is  .
.
In complex numbers of the form 


← Didn't Know|Knew It →
Which of the following represents the real component of the complex number  ?
?
Which of the following represents the real component of the complex number 
Tap to reveal answer
In complex numbers of the form  , a represents the real portion of the number and b represents the imaginary portion of the number. In the complex number
, a represents the real portion of the number and b represents the imaginary portion of the number. In the complex number  ,
,  and
and  .
.
In complex numbers of the form 



← Didn't Know|Knew It →
Which of the following represents the imaginary component of the complex number -3 + ki, in which k is a constant?
Which of the following represents the imaginary component of the complex number -3 + ki, in which k is a constant?
Tap to reveal answer
In complex numbers of the form  ,
,  represents the real portion of the number and
represents the real portion of the number and  represents the imaginary portion of the number. In the complex number
represents the imaginary portion of the number. In the complex number  ,
,  and
and 
In complex numbers of the form 




← Didn't Know|Knew It →
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Tap to reveal answer
In complex numbers of the form  , a represents the real portion of the number and b represents the imaginary portion of the number. To graph
, a represents the real portion of the number and b represents the imaginary portion of the number. To graph  on a plane in which real numbers are represented by the x-axis and imaginary numbers are represented by the y-axis, place a point a units right of the origin and b units above the origin. The graph shows a point 4 units right and 7 units below the origin, so the complex number represented is
on a plane in which real numbers are represented by the x-axis and imaginary numbers are represented by the y-axis, place a point a units right of the origin and b units above the origin. The graph shows a point 4 units right and 7 units below the origin, so the complex number represented is  .
.
In complex numbers of the form 


← Didn't Know|Knew It →
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
Tap to reveal answer
In complex numbers of the form  , a represents the real portion of the number and b represents the imaginary portion of the number. To graph
, a represents the real portion of the number and b represents the imaginary portion of the number. To graph  on a plane in which real numbers are represented by the x-axis and imaginary numbers are represented by the y-axis, place a point a units right of the origin and b units above the origin. The graph shows a point 8 units left and 1 unit above the origin, so the complex number represented is
on a plane in which real numbers are represented by the x-axis and imaginary numbers are represented by the y-axis, place a point a units right of the origin and b units above the origin. The graph shows a point 8 units left and 1 unit above the origin, so the complex number represented is  .
.
In complex numbers of the form 


← Didn't Know|Knew It →
Add:

Add:
Tap to reveal answer
When adding complex numbers, add the real parts and the imaginary parts separately to get another complex number in standard form.
Adding the real parts gives  , and adding the imaginary parts gives
, and adding the imaginary parts gives  .
.
When adding complex numbers, add the real parts and the imaginary parts separately to get another complex number in standard form.
Adding the real parts gives 

← Didn't Know|Knew It →
Subtract:

Subtract:
Tap to reveal answer
This is essentially the following expression after translation:

Now add the real parts together for a sum of  , and add the imaginary parts for a sum of
, and add the imaginary parts for a sum of  .
.
This is essentially the following expression after translation:
Now add the real parts together for a sum of 

← Didn't Know|Knew It →
Multiply:

Answer must be in standard form.
Multiply:
Answer must be in standard form.
Tap to reveal answer

The first step is to distribute which gives us:


which is in standard form.
The first step is to distribute which gives us:
which is in standard form.
← Didn't Know|Knew It →
Divide: 
The answer must be in standard form.
Divide:
The answer must be in standard form.
Tap to reveal answer
Multiply both the numerator and the denominator by the conjugate of the denominator which is  which results in
which results in

The numerator after simplification give us 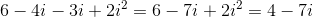
The denominator is equal to 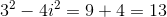
Hence, the final answer in standard form =

Multiply both the numerator and the denominator by the conjugate of the denominator which is 
The numerator after simplification give us
The denominator is equal to
Hence, the final answer in standard form =
← Didn't Know|Knew It →
Divide: 
Answer must be in standard form.
Divide:
Answer must be in standard form.
Tap to reveal answer
Multiply both the numerator and the denominator by the conjugate of the denominator which is  resulting in
resulting in

This is equal to 
Since  you can make that substitution of
you can make that substitution of  in place of
in place of  in both numerator and denominator, leaving:
in both numerator and denominator, leaving:

When you then cancel the negatives in both numerator and denominator (remember that  , simplifying each term), you're left with a denominator of
, simplifying each term), you're left with a denominator of  and a numerator of
and a numerator of  , which equals
, which equals  .
.
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
This is equal to
Since 


When you then cancel the negatives in both numerator and denominator (remember that 



← Didn't Know|Knew It →
What is the absolute value of 
What is the absolute value of
Tap to reveal answer
The absolute value is a measure of the distance of a point from the origin. Using the pythagorean distance formula to calculate this distance.
The absolute value is a measure of the distance of a point from the origin. Using the pythagorean distance formula to calculate this distance.
← Didn't Know|Knew It →
Simplify the expression.

Simplify the expression.
Tap to reveal answer
Combine like terms. Treat  as if it were any other variable.
as if it were any other variable.


Substitute to eliminate  .
.


Simplify.

Combine like terms. Treat 
Substitute to eliminate 
Simplify.
← Didn't Know|Knew It →
Consider the following definitions of imaginary numbers:



Then, 
Consider the following definitions of imaginary numbers:
Then,
Tap to reveal answer
← Didn't Know|Knew It →

Find  .
.
Find 
Tap to reveal answer
Multiply the numerator and denominator by the numerator's complex conjugate.

Reduce/simplify.
Multiply the numerator and denominator by the numerator's complex conjugate.
Reduce/simplify.
← Didn't Know|Knew It →
What is the value of  ?
?
What is the value of 
Tap to reveal answer
Recall that the definition of imaginary numbers gives that  and thus that
and thus that  . Therefore, we can use Exponent Rules to write
. Therefore, we can use Exponent Rules to write 
Recall that the definition of imaginary numbers gives that 

← Didn't Know|Knew It →