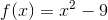Parabolic Functions
Help Questions
Algebra 2 › Parabolic Functions
Consider the equation:
The vertex of this parabolic function would be located at:
Explanation
For any parabola, the general equation is


For the given problem, the x-coordinate is

To find the y-coordinate, plug 
Therefore the vertex is at 
Red line
Blue line
Green line
Purple line
None of them
Explanation
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to 
The blue line represents a linear function and will have a formula similar to 
The green line represents an exponential function and will have a formula similar to 
The purple line represents an absolute value function and will have a formula similar to 
What are the 
There are no 
Explanation
To find the x-intercepts of the equation, we set the numerator equal to zero.
Consider the following two functions:

How is the function 











Explanation
The 


Consider the equation:
The vertex of this parabolic function would be located at:
Explanation
For any parabola, the general equation is


For the given problem, the x-coordinate is

To find the y-coordinate, plug 
Therefore the vertex is at 
Red line
Blue line
Green line
Purple line
None of them
Explanation
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to 
The blue line represents a linear function and will have a formula similar to 
The green line represents an exponential function and will have a formula similar to 
The purple line represents an absolute value function and will have a formula similar to 
Consider the following two functions:

How is the function 











Explanation
The 


What are the 
There are no 
Explanation
To find the x-intercepts of the equation, we set the numerator equal to zero.
Which of the following functions represents a parabola?
Explanation
A parabola is a curve that can be represented by a quadratic equation. The only quadratic here is represented by the function 
A particular parabola has it's vertex at 
None of these
Explanation
General parabola equation:
Vertex formula:
Where 

Combining equations:
Plugging in values for vertex:
Solving for 
Returning to:
combining equations:
Plugging in values of given intercept:
Solving for
Plugging in value:
Plugging in values for the vertex:
Final equation: