Comparing relative magnitudes of functions and their rates of change - AP Calculus AB
Card 1 of 1166
Evaluate the definite integral of the algebraic function.
integral (x3 + √(x))dx from 0 to 1
Evaluate the definite integral of the algebraic function.
integral (x3 + √(x))dx from 0 to 1
Tap to reveal answer
Step 1: Rewrite the problem.
integral (x3+x1/2) dx from 0 to 1
Step 2: Integrate
x4/4 + 2x(2/3)/3 from 0 to 1
Step 3: Plug in bounds and solve.
\[14/4 + 2(1)(2/3)/3\] – \[04/4 + 2(0)(2/3)/3\] = (1/4) + (2/3) = (3/12) + (8/12) = 11/12
Step 1: Rewrite the problem.
integral (x3+x1/2) dx from 0 to 1
Step 2: Integrate
x4/4 + 2x(2/3)/3 from 0 to 1
Step 3: Plug in bounds and solve.
\[14/4 + 2(1)(2/3)/3\] – \[04/4 + 2(0)(2/3)/3\] = (1/4) + (2/3) = (3/12) + (8/12) = 11/12
← Didn't Know|Knew It →
Evaluate the integral.
Integral from 1 to 2 of (1/x3) dx
Evaluate the integral.
Integral from 1 to 2 of (1/x3) dx
Tap to reveal answer
Integral from 1 to 2 of (1/x3) dx
Integral from 1 to 2 of (x-3) dx
Integrate the integral.
from 1 to 2 of (x–2/-2)
(2–2/–2) – (1–2/–2) = (–1/8) – (–1/2)=(3/8)
Integral from 1 to 2 of (1/x3) dx
Integral from 1 to 2 of (x-3) dx
Integrate the integral.
from 1 to 2 of (x–2/-2)
(2–2/–2) – (1–2/–2) = (–1/8) – (–1/2)=(3/8)
← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
In order to evaluate the indefinite integral, ask yourself, "what expression do I differentiate to get 4". Next, use the power rule and increase the power of  by 1. To start, we have
by 1. To start, we have  , so in the answer we have
, so in the answer we have  . Next add a constant that would be lost in the differentiation. To check your work, differentiate your answer and see that it matches "4".
. Next add a constant that would be lost in the differentiation. To check your work, differentiate your answer and see that it matches "4".
In order to evaluate the indefinite integral, ask yourself, "what expression do I differentiate to get 4". Next, use the power rule and increase the power of 


← Didn't Know|Knew It →
Tap to reveal answer
The answer is  . The definition of the derivative of
. The definition of the derivative of  is
is  . Remember to add the
. Remember to add the  to undefined integrals.
to undefined integrals.
The answer is 



← Didn't Know|Knew It →
int_${-1}^{0}$$e^{1-t}$dt =
int_${-1}^{0}$$e^{1-t}$dt =
Tap to reveal answer
We can use the substitution technique to evaluate this integral.
Let  .
.
We will differentiate  with respect to
with respect to  .
.
 , which means that
, which means that  .
.
We can solve for  in terms of
in terms of  , which gives us
, which gives us  .
.
We will also need to change the bounds of the integral. When  ,
,  , and when
, and when  ,
,  .
.
We will now substitute  in for the
in for the  , and we will substitute
, and we will substitute  for
for  .
.
int_${2}^{1}$$-e^{u}$du
int_${2}^{1}$$-e^{u}$du = $-e^{u}$|_${2}^{1}$$=-e^{1}$$-(-e^{2}$$)=e^{2}$$-e^{1}$
The answer is $e^{2}$-e.
We can use the substitution technique to evaluate this integral.
Let 
We will differentiate 



We can solve for 


We will also need to change the bounds of the integral. When 



We will now substitute 



int_${2}^{1}$$-e^{u}$du
int_${2}^{1}$$-e^{u}$du = $-e^{u}$|_${2}^{1}$$=-e^{1}$$-(-e^{2}$$)=e^{2}$$-e^{1}$
The answer is $e^{2}$-e.
← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
Use the inverse Power Rule to evaluate the integral. We know that  for
for  . We see that this rule tells us to increase the power of
. We see that this rule tells us to increase the power of  by 1 and multiply by
by 1 and multiply by  . Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Use the inverse Power Rule to evaluate the integral. We know that 



← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
Use the inverse Power Rule to evaluate the integral. We know that  for
for  . We see that this rule tells us to increase the power of
. We see that this rule tells us to increase the power of  by 1 and multiply by
by 1 and multiply by  . Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Use the inverse Power Rule to evaluate the integral. We know that 



← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
Use the inverse Power Rule to evaluate the integral. Firstly, constants can be taken out of integrals, so we pull the 3 out front. Next, according to the inverse power rule, we know that  for
for  . We see that this rule tells us to increase the power of
. We see that this rule tells us to increase the power of  by 1 and multiply by
by 1 and multiply by  . Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Use the inverse Power Rule to evaluate the integral. Firstly, constants can be taken out of integrals, so we pull the 3 out front. Next, according to the inverse power rule, we know that 



← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
Use the inverse Power Rule to evaluate the integral. We know that  for
for  . We see that this rule tells us to increase the power of
. We see that this rule tells us to increase the power of  by 1 and multiply by
by 1 and multiply by  . Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Use the inverse Power Rule to evaluate the integral. We know that 



← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
Use the inverse Power Rule to evaluate the integral. We know that  for
for  . We see that this rule tells us to increase the power of
. We see that this rule tells us to increase the power of  by 1 and multiply by
by 1 and multiply by  Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Use the inverse Power Rule to evaluate the integral. We know that 



← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
Use the inverse Power Rule to evaluate the integral. Firstly, constants can be taken out of the integral, so we pull the 1/2 out front and then complete the integration according to the rule. We know that  for
for  . We see that this rule tells us to increase the power of
. We see that this rule tells us to increase the power of  by 1 and multiply by
by 1 and multiply by  . Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Use the inverse Power Rule to evaluate the integral. Firstly, constants can be taken out of the integral, so we pull the 1/2 out front and then complete the integration according to the rule. We know that 



← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
Use the inverse Power Rule to evaluate the integral. We know that  for
for  . But, in this case,
. But, in this case,  IS equal to
IS equal to  so a special condition of the rule applies. We must instead use
so a special condition of the rule applies. We must instead use  . Evaluate accordingly. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
. Evaluate accordingly. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Use the inverse Power Rule to evaluate the integral. We know that 




← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
Use the inverse Power Rule to evaluate the integral. We know that  for
for  . But, in this case,
. But, in this case,  IS equal to
IS equal to  so a special condition of the rule applies. We must instead use
so a special condition of the rule applies. We must instead use  . Pull the constant "3" out front and evaluate accordingly. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
. Pull the constant "3" out front and evaluate accordingly. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.
Use the inverse Power Rule to evaluate the integral. We know that 




← Didn't Know|Knew It →
Evaluate the following definite integral.

Evaluate the following definite integral.
Tap to reveal answer
Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 0 to 2. First, we use our inverse power rule to find the antiderivative. So, we have that  . Once you find the antiderivative, we must remember that
. Once you find the antiderivative, we must remember that 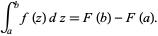 where
where  is the indefinite integral. So, we plug in our limits and subtract the two. So, we have
is the indefinite integral. So, we plug in our limits and subtract the two. So, we have  .
.
Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 0 to 2. First, we use our inverse power rule to find the antiderivative. So, we have that 
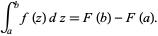 where
where 

← Didn't Know|Knew It →
Evaluate the following definite integral.

Evaluate the following definite integral.
Tap to reveal answer
Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 1 to 3. First, we use our inverse power rule to find the antiderivative. So, we have that  . Once you find the antiderivative, we must remember that
. Once you find the antiderivative, we must remember that 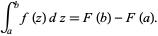 where
where  is the indefinite integral. So, we plug in our limits and subtract the two. So, we have
is the indefinite integral. So, we plug in our limits and subtract the two. So, we have  .
.
Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 1 to 3. First, we use our inverse power rule to find the antiderivative. So, we have that 
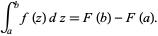 where
where 

← Didn't Know|Knew It →
Evaluate the following definite integral.

Evaluate the following definite integral.
Tap to reveal answer
Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 1 to 4. First, we use our inverse power rule to find the antiderivative. So since  is to the power of
is to the power of  , we have that
, we have that  . Once you find the antiderivative, we must remember that
. Once you find the antiderivative, we must remember that 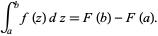 where
where  is the indefinite integral. So, we plug in our limits and subtract the two. So, we have
is the indefinite integral. So, we plug in our limits and subtract the two. So, we have  because we know that
because we know that  .
.
Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 1 to 4. First, we use our inverse power rule to find the antiderivative. So since 


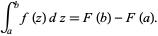 where
where 


← Didn't Know|Knew It →
Tap to reveal answer
The integral of  is
is  . The constant 3 is simply multiplied by the integral.
. The constant 3 is simply multiplied by the integral.
The integral of 

← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
The first step is to find the antiderivative, recalling that:
 .
.
For this integral:
 ,
,
where the intergral would be evaluated from  to
to  (the absolute value bar is not necessary, since both limits of integration are greater than zero):
(the absolute value bar is not necessary, since both limits of integration are greater than zero):



The first step is to find the antiderivative, recalling that:

For this integral:

where the intergral would be evaluated from 

← Didn't Know|Knew It →
Evaluate the following indefinite integral:

Evaluate the following indefinite integral:
Tap to reveal answer
Use substitution, where  and
and  . Thus, the integral can be rewritten as:
. Thus, the integral can be rewritten as:
 .
.
Substitution of  back into this expression gives the final answer:
back into this expression gives the final answer:

Note that since this is an indefinite integral, the addition of a constant term (C) is required.
Use substitution, where 


Substitution of 
Note that since this is an indefinite integral, the addition of a constant term (C) is required.
← Didn't Know|Knew It →
Evaluate the following indefinite integral.

Evaluate the following indefinite integral.
Tap to reveal answer
First, we know that we can pull the constant "4" out of the integral, and we then evaluate the integral according to this equation:
 . From this, we acquire the answer above. As a note, we cannot forget the constant of integration
. From this, we acquire the answer above. As a note, we cannot forget the constant of integration  which would be lost during the differentiation.
which would be lost during the differentiation.
First, we know that we can pull the constant "4" out of the integral, and we then evaluate the integral according to this equation:


← Didn't Know|Knew It →

