Functions - AP Calculus AB
Card 0 of 43260
Let 
What is the Midpoint Riemann Sum on the interval ![[0, 8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/368167/gif.latex) divided into four sub-intervals?
divided into four sub-intervals?
Let
What is the Midpoint Riemann Sum on the interval ![[0, 8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/368167/gif.latex)
The interval ![[0,8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/368151/gif.latex) divided into four sub-intervals gives rectangles with vertices of the bases at
divided into four sub-intervals gives rectangles with vertices of the bases at

For the Midpoint Riemann sum, we need to find the rectangle heights which values come from the midpoint of the sub-intervals, or f(1), f(3), f(5), and f(7).




Because each interval has width 2, the approximated Midpoint Riemann Sum is

The interval ![[0,8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/368151/gif.latex)
For the Midpoint Riemann sum, we need to find the rectangle heights which values come from the midpoint of the sub-intervals, or f(1), f(3), f(5), and f(7).
Because each interval has width 2, the approximated Midpoint Riemann Sum is
Compare your answer with the correct one above
Estimate the area under the curve for the following function using a midpoint Riemann sum from  to
to  with
with  .
.

Estimate the area under the curve for the following function using a midpoint Riemann sum from 


If we want to estimate the area under the curve from  to
to  and are told to use
and are told to use  , this means we estimate the area using two rectangles that will each be two units wide and whose height is the value of the function at the midpoint of the interval. We have a rectangle from
, this means we estimate the area using two rectangles that will each be two units wide and whose height is the value of the function at the midpoint of the interval. We have a rectangle from  to
to  , whose height is the value of the function at
, whose height is the value of the function at  , and a rectangle from
, and a rectangle from  to
to  , whose height is the value of the function at
, whose height is the value of the function at  . First we can find the value of the function at these midpoints, and then add the areas of the two rectangles, which gives us the following:
. First we can find the value of the function at these midpoints, and then add the areas of the two rectangles, which gives us the following:



If we want to estimate the area under the curve from 








Compare your answer with the correct one above
Estimate the area under the curve for the following function from  to
to  using a midpoint Riemann sum with
using a midpoint Riemann sum with  rectangles:
rectangles:

Estimate the area under the curve for the following function from 


If we are told to use  rectangles from
rectangles from  to
to  , this means we have a rectangle from
, this means we have a rectangle from  to
to  , a rectangle from
, a rectangle from  to
to  , a rectangle from
, a rectangle from  to
to  , and a rectangle from
, and a rectangle from  to
to  . We can see that the width of each rectangle is
. We can see that the width of each rectangle is  because we have an interval that is
because we have an interval that is  units long for which we are using
units long for which we are using  rectangles to estimate the area under the curve. The height of each rectangle is the value of the function at the midpoint for its interval, so first we find the height of each rectangle and then add together their areas to find our answer:
rectangles to estimate the area under the curve. The height of each rectangle is the value of the function at the midpoint for its interval, so first we find the height of each rectangle and then add together their areas to find our answer:





If we are told to use 













Compare your answer with the correct one above
Find the area under  on the interval
on the interval ![[0,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/352150/gif.latex) using five midpoint Riemann sums.
using five midpoint Riemann sums.
Find the area under 
![[0,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/352150/gif.latex)
The problem becomes this:

Addings these rectangles up to approximate the area under the curve is

![A=0.2[(1-0.1^2)+(1-0.3^2)+(1-0.5^2)+(1-0.7^2)+(1-0.9^2)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/352152/gif.latex)
![A=0.2[5-0.1^2-0.3^2-0.5^2-0.7^2-0.9^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/352153/gif.latex)
![A=0.2[3.35]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/352154/gif.latex)

The problem becomes this:

Addings these rectangles up to approximate the area under the curve is
Compare your answer with the correct one above
Approximate the area under the curve from  using the midpoint Riemann Sum with a partition of size five given the graph of the function.
using the midpoint Riemann Sum with a partition of size five given the graph of the function.

Approximate the area under the curve from 

We begin by finding the given change in x:

We then define our partition intervals:
![[x_{i-1},x_i]=[0,1.6),[1.6,3.2),[3.2,4.8),[4.8,6.4),[6.4,8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/358807/gif.latex)
We then choose the midpoint in each interval:

Then we find the value of the function at the point. This is determined through observation of the graph

Then we simply substitute these values into the formula for the Riemann Sum

We begin by finding the given change in x:
We then define our partition intervals:
We then choose the midpoint in each interval:
Then we find the value of the function at the point. This is determined through observation of the graph
Then we simply substitute these values into the formula for the Riemann Sum
Compare your answer with the correct one above
Approximate the area underneath the given curve using the Riemann Sum with eight intervals for  .
.

Approximate the area underneath the given curve using the Riemann Sum with eight intervals for 
We begin by defining the size of our partitions and the partitions themselves.

![[x_{i-1},x_i]=[-4,-2],[-2,0],[0,2],[2,4],[4,6],[6,8],[8,10],[10,12]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/359075/gif.latex)
We then choose the midpoint in each interval:

Then we find the function value at each point.

We then substitute these values into the Riemann Sum formula.

We begin by defining the size of our partitions and the partitions themselves.
We then choose the midpoint in each interval:
Then we find the function value at each point.
We then substitute these values into the Riemann Sum formula.
Compare your answer with the correct one above
Solve the integral

using the midpoint Riemann sum approximation with  subintervals.
subintervals.
Solve the integral
using the midpoint Riemann sum approximation with 
Midpoint Riemann sum approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx (\frac{b-a}{n})\left [ f({m_{1}})+f({m_{2}})+...+f({m_{n}}) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361629/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The approximate value at each midpoint is below.

The sum of all the approximate midpoints values is  , therefore
, therefore
![(\frac{b-a}{n})\left [ f({m_{1}})+f({m_{2}})+...+f({m_{n}}) \right ] =0.4(2.116738)\approx0.8467](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361631/gif.latex)
Midpoint Riemann sum approximations are solved using the formula
where 

For this problem, 
The approximate value at each midpoint is below.

The sum of all the approximate midpoints values is 
Compare your answer with the correct one above
Solve the integral

using the midpoint Riemann sum approximation with  subintervals.
subintervals.
Solve the integral
using the midpoint Riemann sum approximation with 
Midpoint Riemann sum approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx (\frac{b-a}{n})\left [ f({m_{1}})+f({m_{2}})+...+f({m_{n}}) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361633/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The approximate value at each midpoint is below.

The sum of all the approximate midpoints values is  , therefore
, therefore
![(\frac{b-a}{n})\left [ f({m_{1}})+f({m_{2}})+...+f({m_{n}}) \right ] =0.7(20.6068259)\approx14.4248](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361635/gif.latex)
Midpoint Riemann sum approximations are solved using the formula
where 

For this problem, 
The approximate value at each midpoint is below.

The sum of all the approximate midpoints values is 
Compare your answer with the correct one above
Solve the integral

using the midpoint Riemann sum approximation with  subintervals.
subintervals.
Solve the integral
using the midpoint Riemann sum approximation with 
Midpoint Riemann sum approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx (\frac{b-a}{n})\left [ f({m_{1}})+f({m_{2}})+...+f({m_{n}}) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361633/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The approximate value at each midpoint is below.

The sum of all the approximate midpoints values is  , therefore
, therefore
![(\frac{b-a}{n})\left [ f({m_{1}})+f({m_{2}})+...+f({m_{n}}) \right ] =0.1571(6.37275)\approx1](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361644/gif.latex)
Midpoint Riemann sum approximations are solved using the formula
where 

For this problem, 
The approximate value at each midpoint is below.

The sum of all the approximate midpoints values is 
Compare your answer with the correct one above
Solve the integral

using the midpoint Riemann sum approximation with  subintervals.
subintervals.
Solve the integral
using the midpoint Riemann sum approximation with 
Midpoint Riemann sum approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx (\frac{b-a}{n})\left [ f({m_{1}})+f({m_{2}})+...+f({m_{n}}) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361633/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The approximate value at each midpoint is below.

The sum of all the approximate midpoints values is  , therefore
, therefore
![(\frac{b-a}{n})\left [ f({m_{1}})+f({m_{2}})+...+f({m_{n}}) \right ] =0.3(468.3221)\approx140.4966](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361647/gif.latex)
Midpoint Riemann sum approximations are solved using the formula
where 

For this problem, 
The approximate value at each midpoint is below.

The sum of all the approximate midpoints values is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369004/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.5)*(0.86027754)=0.4301](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369006/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369007/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.1)*(28.786699)=2.8787](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361699/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx =T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361690/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.4)*(83.89553)=33.5582](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361706/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/368964/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.1)*(11.7257431)=1.1726](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361709/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx =S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361760/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.4)*(-8.23995)=-1.0987](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361762/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx=S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361739/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.7)*(72.79378)=16.9852](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361741/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx =S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361742/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.2)*(10.5840)=0.7056](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361744/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx\approx S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361736/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.9)*(2.3081)=0.6924](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361757/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Using a midpoint Reimann sum with  , estimate the area under the curve from
, estimate the area under the curve from 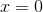 to
to  for the following function:
for the following function:

Using a midpoint Reimann sum with 
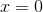


Thus, our intervals are  to
to  ,
,  to
to  , and
, and  to
to  .
.
The midpoints of each interval are, respectively,  ,
,  , and
, and  .
.
Next, we evaluate the function at each midpoint.




Finally, we calculate the estimated area using these values and 


Thus, our intervals are 





The midpoints of each interval are, respectively, 


Next, we evaluate the function at each midpoint.
Finally, we calculate the estimated area using these values and
Compare your answer with the correct one above

The table above gives the values for a function at certain points.
Using the data from the table, find the midpoint Riemann sum of  with
with  , from
, from 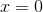 to
to  .
.
The table above gives the values for a function at certain points.
Using the data from the table, find the midpoint Riemann sum of 

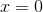


Thus, our intervals are  to
to  ,
,  to
to  , and
, and  to
to  .
.
The midpoints of each interval are, respectively,  ,
,  , and
, and  .
.
Next, use the data table to take the values the function at each midpoint.



Finally, we calculate the estimated area using these values and  .
.


Thus, our intervals are 





The midpoints of each interval are, respectively, 


Next, use the data table to take the values the function at each midpoint.
Finally, we calculate the estimated area using these values and 
Compare your answer with the correct one above