Impulse and Momentum - AP Physics 1

Card 0 of 340

Question

Two sumo wrestlers are in a match. At the start of the match, they both lunge at each other. They hit and miraculously come to a stand still. One wrestler was 200kg and traveling at a velocity of $2.3\frac{m}{s}$ at the instance of collision. If the other wrestler was traveling at $2.9\frac{m}{s}$ , what is his mass?

Answer

It does not matter whether the collision is elastic or inelastic (although it would be best to assume that it's inelastic). Momentum is conserved in either type of collision, and is the only value needed for our calculation. Since they come to a standstill, their momentums at the moment of collision are equal and opposite:

Rearrange to solve for :

$m_1=\frac{m_2v_2}{v_1}$

Plug in the given values from the question and solve:

$m_1=\frac{(200kg)(2.3\frac{m}{s})}{2.9\frac{m}{s}}$

Compare your answer with the correct one above

Question

One car with a mass of 400kg is traveling east at $20\frac{m}{s}$ and collides with a car of mass 800kg traveling west at $15\frac{m}{s}$ . Assuming the collision is completely inellastic, what is velocity of the first car after the collision?

Answer

Since the collision is completely inelastic, momentum is conserved but energy is not. Furthermore, the two cars stick to each other and travel as one. The equation for conservation of momentum is as follows:

There are two inital masses with different velocities and one final mass with a single velocity. Therefore, we can write:

Rearranging for final velocity, we get:

$v = \frac{m_1v_1 + m_2v_2}{m}$

At this point, we can denote which direction is positive and which is negative. Since the car traveling west has more momentum, we will consider west to be positive. Substituting our values into the equation, we get:

$v = \frac{(400)(-20)+ (800)(15)}{400 + 800}$

$v = \frac{-800 + 12000}{1200} = \frac{4000}{1200} = 3.33\frac{m}{s}$

Since this value is positive, the final answer is $3.33\frac{m}{s}$ West.

Compare your answer with the correct one above

Question

A popular topic in early space exploration was how to safely return modules back to the surface of the earth. Early designs contained materials that could only withstand impulses of up to $4500 \frac{kg\cdot m}{s}$ before parts of the module became compromised. One such model of mass 500kg is approaching ocean waters and deploys its shoot, reducing its speed to $8 \frac{m}{s}$ . If the module decelerates to zero velocity in 0.9 seconds upon hitting the water, is the module structurally compromised?

$g=10\frac{m}{s^2}$

Answer

We need to use the equation for impulse to solve this problem. In fact, the time given is completely irrevelevant:

$I =F\cdot t = m \Delta v$

Plugging in our values:

$I = (500kg)(8\frac{m}{s}) = 4000 \frac{kg\cdot m}{s}$

This is less than the threshold, so no, nothing becomes structurally compromised

Compare your answer with the correct one above

Question

In a billiards game, one player hits the cue ball towards another ball. The cue ball has a mass of 0.1kg and hits the other ball with a velocity of $2\frac{m}{s}$ . If the collision is completely elastic and the cue ball travels with a velocity of $0.8\frac{m}{s}$ after the collision, what is the mass and velocity of the other ball?

Answer

Since the collision is completely elastic, we know that both momentum and kinetic energy are conserved. We can write the following equations (initial momentum and energy of the second ball are neglected since it is not moving:

$\frac{1}{2}m_1v_i^2= \frac{1}{2}m_1v_f^2+\frac{1}{2}m_2v_2^2$

Rearrange the first equation for and the second for .

$m_2=\frac{m_1(v_i-v_f)}{v_2}$

$v_2^2=\frac{m_1(v_i^2-v_f^2)}{m_2}$

We can rewrite the second equation as:

$v_2^2=\frac{m_1(v_i+v_f)(v_i-v_f)}{m_2}$

Substitute our equation for into the second equation:

$v_2^2=\frac{m_1(v_i-v_f)(v_i+v_f)}{\frac{m_1(v_i-v_f)}{v_2}}$

Rearranging, we get:

$v_2^2=\frac{m_1(v_i-v_f)(v_i+v_f)}{m_1(v_i-v_f)v_2^{-1}}=\frac{(v_i+v_f)}{v_2^{-1}}$

Plug in our values for the initial and final velocities:

$v_2=(2\frac{m}{s}+0.8\frac{m}{s})$

$v_2=2.8\frac{m}{s}$

To solve for mass, we'll use our earlier expression for :

$m_2=\frac{m_1(v_i-v_f)}{v_2}$

$m_2= \frac{(0.1kg)(2\frac{m}{s}-0.8\frac{m}{s})}{2.8\frac{m}{s}}= 0.043kg$

Compare your answer with the correct one above

Question

A marble of mass falls off a bed with a height of . What is the impulse on the marble as it hits the ground?

$g = 10\frac{m}{s^2}$

Answer

Impulse can be written as either of two popular expressions:

$I = F\Delta t = m\Delta v$

From the problem statement, we can determine the velocity of the marble as it hits the floor, allowing us to use the latter expression. To determining the velocity of the marble, we can use the equation for conservation of energy:

Assuming the final height is zero, we can eliminate initial kinetic energy and final potential energy. Therefore, we can write:

$mgh_i = \frac{1}{2}mv_f^2$

Canceling out mass and rearranging for final velocity, we get:

$v_f = \sqrt{2gh_i}$

We know these variables, allowing us to solve for the velocity:

$v_f = \sqrt{2(10\frac{m}{s^2})(1.2m)} = 4.9\frac{m}{s}$

Plugging this value into the expression for impulse, we get:

$I = (0.1kg)(4.9\frac{m}{s})= 0.49 N\cdot s$

Compare your answer with the correct one above

Question

Consider the following system:

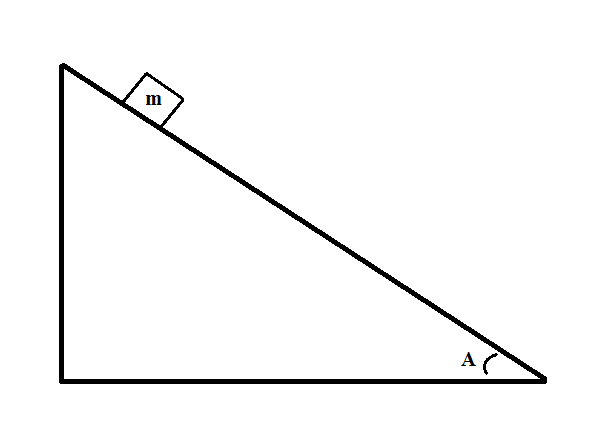
If the block has a mass of , the angle measures $50^{\circ}$ , and there is no friction between the block and slope, what is the momentum of the block after it has traveled a horizontal distance of ?

Answer

To calculate the momentum of the block, we first need to know the velocity of the block. This can be found using the equation for the conservation of momentum:

If we assume that the final height is zero, we can eliminate initial kinetic energy and final potential energy, getting:

Substituting expressions for each term, we get:

$mgh_i = \frac{1}{2}mv_f^2$

Cancel out mass and rearrange to solve for velocity:

$v_f = \sqrt{2gh_i} = \sqrt{2(10\frac{m}{s^2})(h_i)}$

We can use the horizontal distance traveled and the angle of the slope to determine the initial height:

$tan(A) = \frac{h_i}{horizontal}$

$h_i = tan(A)\cdot horizontal$

$h_i = tan(50^{\circ})*10m = 11.9m$

Now that we have the initial height, we can solve for final velocity:

$v_f = \sqrt{2(10\frac{m}{s^2})(11.9m)} = 15.4\frac{m}{s}$

Finally, we can now use the equation for momentum to solve the problem:

$p = m\Delta v$

$p = (20kg)(15.4\frac{m}{s})$

$p = 309 \frac{kg\cdot m}{s}$

Compare your answer with the correct one above

Question

Two astronauts in space are traveling directly towards each other. Astronaut A has a mass of and a velocity of $15\frac{m}{s}$ and Astronaut B has a mass of and a velocity of $5\frac{m}{s}$ . When the astronauts collide, they grab onto each other. What is the velocity of the two astronauts after the collision as they continue to grab onto each other?

Answer

Momentum is always conserved. Equation for conservation of momentum:

$m_{1}v_{1}+m_{2}v_{2}=(m_{1}+m_{2})v_{total}$

There is only one velocity on the right since the two astronauts grab onto each other, thus they move together at the same velocity. Solve.

$(70kg\cdot15\frac{m}{s})+(60kg(-5\frac{m}{s}))=(70kg+60kg)v_{total}$

$v_{total}=5.77\frac{m}{s}$

Compare your answer with the correct one above

Question

Tom drops a ball of mass from rest from a height . The ball bounces back to a height of $\frac{h}{2}$ . Find the magnitude of the impulse the ground imparted on the ball.

Answer

Impulse is just the change in momentum. To find the velocity when the ball hits the ground, we need to use kinematics. We know the height the ball is dropped, the acceleration, and the initial velocity, so we can use the equation $v_{final}^2=v_{initial}^2+2a\Delta x$ . The initial velocity is , , and $\Delta x=h$ , so the equation becomes $v_{final}^2=2gh$

$v_{final}=\sqrt{2gh}$

When the ball bounces back up it reaches a height of $\frac{h}{2}$ . In order to find the velocity immediately after it hits the ground, we can use the same equation with $\Delta x=\frac{h}{2}$ . This will lead it a velocity of $\sqrt{2g*\frac{h}{2}}=\sqrt{gh}$

Assuming up is positive, the magnitude of the impulse is just $m\left | \sqrt{gh}-(-\sqrt{2gh})\right |=(1+\sqrt{2})m\sqrt{gh}$

Compare your answer with the correct one above

Question

Joe, of mass 90kg, jumps straight up. To do so, he bends his knees and produces an upwards force that results in a constant upward net force of 100N. If Joe experiences this force for 0.9s before leaving the ground, what is Joe's velocity immediately after he leaves the ground?

Answer

To solve this problem we need to use the relationship between force and impulse, which is given by the following equation:

$F=\frac{\Delta P}{t}$

This equation represents that the rate of change of momentum with respect to time is equal to the net force that causes said change in momentum. Thus:

$F=\frac{P_f-P_i}{t}=\frac{mV_f-mV_i}{t}$

Note that Joe must have an initial velocity of $0\frac{m}{s}$ before he begins to apply the upwards Force that accelerates him upwards, therefore our equation simplifies to:

$F=\frac{mV_f}{t}$

Solve for :

$V_f=\frac{Ft}{m}=\frac{(100N)(0.9s)}{90kg}=\frac{90kg\cdot \frac{m}{s}}{90kg}=1\frac{m}{s}$

Compare your answer with the correct one above

Question

Which of the following explains why when we land on our feet, we instinctively bend our knees? Hint: think about the relationship between force, impulse, and time.

Answer

Say that, when we hit the ground, we have a velocity , which is predetermined by whatever happens before the impact. When we hit the ground you will experience a force for some time. This force will cause the acceleration that reduces our velocity to zero and gets us to stop. Note that, regardless of how much time it takes us to stop, the change in momentum (impulse) is fixed, since it directly depends on how much our velocity changes:

$P_f=\frac{0kg\cdot m}{s}$ (since we come to a stop)

Note that the initial momentum does not depend on the impact force nor on how much time it takes to stop. The initial momentum depends on the velocity we have when we first hit the ground. This velocity is given by whatever happened before we hit the ground, which no longer concerns us since we only care about what happens from the moment we first hit the ground till the moment we stop. Yes, the time that passes for you to stop is very small, but it is impossible for it to be zero. So we have that the change in momentum (impulse) is a constant:

$\Delta P=-mv= constant$ , since is predetermined.

Remember that any change in momentum for a given mass occurs because its velocity changes. The velocity of the mass changes due to an acceleration and an acceleration is caused by a force. This gives us a relationship between force and impulse:

$F=\Delt\frac{\Delta P}{t}$

In our scenario, would be the impact force that stops us and the time it takes us to stop. From the equation above, it is easy to see that, since $\Delta P$ is fixed, when gets larger gets smaller, and the other way around. Therefore, we bend our knees to effectively increase the time it takes us to stop. Thus, diminishing the impact force as to avoid hurting ourselves.

Compare your answer with the correct one above

Question

When catching an object, an average person can stand a maximum impact force of 20000N. Forces greater than this would most likely break bones in the person's hand. If a person catches a 500g baseball that moves at $-50\frac{m}{s}$ , what is the minimum time the person should take to stop it in order to avoid seriously hurting his hand?

Answer

In order to solve this problem we need to use the relationship between force and impulse:

$F=\frac{\Delta P}{t}$

Since the ball is moving with a Velocity of $-50\frac{m}{s}$ , we have that

$\Delta P=P_f-P_i=mV_f-mV_i$

$\Delta P=(0.5kg)(0 \frac{m}{s})-(0.5kg)(-50\frac{m}{s})=\frac{25kg\cdot m}{s}$

Note that the final velocity of the ball is zero since it comes to a stop. We want the force, , experienced by the person's hand to be less than or equal to the maximum impact force

Mathematically:

$F\leq F_i_m_p$

$\frac{1}{F}\geq \frac{1}{F_i_m_p}$

Use the impulse equation and solve for time:

$t=\frac{\Delta P}{F}\geq \frac{\Delta P}{F_i_m_p}$

$t\geq \frac{\frac{25kg\cdot m}{s}}{20000N}=1.25*10^{-3}s$

Compare your answer with the correct one above

Question

A billiard ball travels at $v_{1}=v$ toward another billiard ball traveling at $v_{2}=-2v$ . They collide elastically. Which option correctly describes the final velocities of the billiard balls? Assume they have the same mass.

Answer

Due to conservation of momentum, the initial momentum must equal the final momentum of the system. Both billiard balls are of equal mass, and since the collision is elastic than the billiard balls will simply exchange momentum. This is a problem that is best to think about before starting to solve any equations because sometimes the correct answer is one you can deduce without any calculations. Therefore:

$v_{1f}=-2v$

$v_{2f}=v$

Compare your answer with the correct one above

Question

A 150g baseball is thrown with a speed of $40: \frac{m}{s}$ . If it takes 0.7s for the baseball to come to rest in the catcher's glove, what is the average force the catcher experiences due to the ball?

Answer

To solve this problem, we need to consider the change in the ball's momentum. To do so, we'll use the following equation.

$J=m\Delta v=F_{avg}t$

Rearrange the above equation to solve for the average force.

$F_{avg}=\frac{m\Delta v}{t}=\frac{(0.15 kg)(40 \frac{m}{s})}{0.7 s}$

$F_{avg}=8.57N$

Compare your answer with the correct one above

Question

A rock flying through the air is traveling at a velocity of $12\frac{m}{s}$ when it collides into and sticks to a stationary bean bag, weighing . What is the velocity of the two objects?

Answer

The equation for momentum is:

To maintain conservation of momentum, a new state must have the same momentum as a previous state:

$m_{1i}v_{1i}+m_{2i}v_{2i}=m_{1f}v_{1f}+m_{2f}v_{2f}$

Since the rock and the bean bag move together after the collision, $v_{1f}=v_{2f}$ . And since the bean bag is initially stationary, $v_{2i}=0$

Plug in known values and solve.

$5kg(12\frac{m}{s})+20kg(0)=(5kg+20kg)(v_f)$

$60\frac{kgm}{s}=25kg(v_f)$

$v_f=2.4\frac{m}{s}$

Compare your answer with the correct one above

Question

An asteroid of mass is traveling with the velocity $<391, 498, 121> \frac{m}{s}$ .

What is the magnitude of the momentum of the asteriod?

Answer

First, we will need to find the magnitude of the velocity vector.

$\left | \vec{v} \right |=\sqrt{v_x^2+v_y^2+v_z^2}$

Plugging in our values

$\left | \vec{v} \right |=\sqrt{391^2+498^2+121^2}$

$645 \frac{m}{s}=|\vec{v}|$

Momemtum is defined as

$\vec{P}=m\vec{v}$

Thus,

$\left | \vec{P} \right | =m \left | \vec{v} \right |$

We plug in our values

$\left | \vec{P} \right | =560kg\cdot \left | 645\frac{m}{s}\right |$

$3.6\times10^5 kg\frac{m}{s}=|\vec{P}|$

Compare your answer with the correct one above

Question

A train of mass $1.8\times10^7 kg$ traveling at $15 \frac{m}{s}$ strikes a car stuck on the tracks of mass .

Determine the initial momentum of the system.

Answer

$P_{total}=P_1+P_2.......$

The train and car are our only two objects in the system.

The initial momentum of the car is zero.

So the only momentum that will contribute is that of the train.

$p=1.8\times10^7\cdot15$

Plugging in our values, we get $2.7\times10^8 kg\frac{m}{s}$

Compare your answer with the correct one above

Question

A locomotive of mass traveling at $4\frac{km}{hr}$ couples to a motionless coach without applying the brakes. Calculate the momentum change (the impulse experienced) of the coach.

Answer

Use conservation of momentum

$m_{1i}v_{1i}+m_{2i}v_{2i}=m_{1,2f}v_{1,2f}$

Plug in values:

$(16710^3)4+(6710^3)0=(23410^3)v_{1,2f}$

Solve for $v_{1,2f}$ :

$v_{1,2f}=\frac{16710^34}{23410^3}$

$v_{1,2f}=2.85\frac{km}{hr}$

Definition of impulse:

$J=\Delta P=m(v_f-v_i)$

Convert $\frac{km}{hr}$ to $\frac{m}{s}$

$2.85\frac{km}{hr}\frac{1hr}{3600s}\frac{1000m}{1km}=.79\frac{m}{s}$

Plug in values:

$J=\Delta P=6710^3(.79-0)$

$J=52.310^3\frac{kg*m}{s}$

Compare your answer with the correct one above

Question

A train of mass $1.8\times10^7 kg$ traveling at $15 \frac{m}{s}$ strikes a car stuck on the tracks of mass . The car becomes stuck on the train.

Determine the final velocity of the train.

Answer

We will need to use conservation of momentum to solve this problem.

$M_1V_1+M_2V_2=M_{final}V_{final}$

Where and refer to the train, and and refer to the car. $M_{final}$ and $V_{final}$ refer to the final state of both the train and the car.

Rearranging using algebra......

$\frac{M_1V_1+M_2V_2}{M_{final}}=V_{final}$

$\frac{1.8\times10^7\cdot15+1300\cdot0}{1.8\times10^7}=V_{final}$

Plugging in our values, we get $15 \frac{m}{s}$ .

Compare your answer with the correct one above

Question

A train of mass $1.8\times10^7 kg$ traveling at $15 \frac{m}{s}$ strikes a car stuck on the tracks of mass . The car becomes stuck on the train.

Determine the final velocity of the car.

Answer

We will need to use conservation of momentum to solve this problem.

$M_1V_1+M_2V_2=M_{final}V_{final}$

Where and refer to the train, and and refer to the car. $M_{final}$ and $V_{final}$ refer to the final state of both the train and the car.

Rearranging using algebra......

$\frac{M_1V_1+M_2V_2}{M_{final}}=V_{final}$

$\frac{1.8\times10^7\cdot15+1300\cdot0}{1.8\times10^7}=V_{final}$

Plugging in our values, we get $15 \frac{m}{s}$ .

Compare your answer with the correct one above

Question

A train of mass $1.8\times10^7 kg$ traveling at $15 \frac{m}{s}$ strikes a car stuck on the tracks of mass .

Let's assume this collison took to happen. That is, it took the car to accelerate to it's new velocity. Determine the force experienced by the car.

Answer

We will need to use conservation of momentum to solve this problem.

$M_1V_1+M_2V_2=M_{final}V_{final}$

Where and refer to the train, and and refer to the car. $M_{final}$ and $V_{final}$ refer to the final state of both the train and the car.

Rearranging using algebra......

$\frac{M_1V_1+M_2V_2}{M_{final}}=V_{final}$

$\frac{1.8\times10^7\cdot15+1300\cdot0}{1.8\times10^7}=V_{final}$

Plugging in our values, we get $15 \frac{m}{s}$ .

Then, we will need to find out final momentum of the car.

$M_{car}V_{final}=P_{final}$

$1300kg\cdot15\frac{m}{s}=P_{final}$

$M_{car}V_{final}=P_{final}$

$\Delta P=P_{final}-P_{initial}$

Since our intial momentum of the car was , our change in momentum will be equal to the $P_{final}$ .

$\Delta P=P_{final}$

We will use the definition of impulse, which is the change in momentum:

$F\cdot \Delta t= \Delta P$

We will use substitution:

$F\cdot \Delta t= P_{final}$

Plugging in our values, we get $1.95\times10^6 N$

Compare your answer with the correct one above

Tap the card to reveal the answer