Rotational Motion and Torque - AP Physics C: Electricity and Magnetism
Card 1 of 319
An object starts from rest and accelerates to an angular velocity of  in three seconds under a constant torque of
in three seconds under a constant torque of  . How many revolutions has the object made in this time?
. How many revolutions has the object made in this time?
An object starts from rest and accelerates to an angular velocity of 

Tap to reveal answer
Since it is experiencing a constant torque and constant angular acceleration, the angular displacement can be calculated using:

The angular acceleration is easily calculated using the angular velocity and the time:

Using this value, we can find the angular displacement:


Convert the angular displacement to revolutions by diving by  :
:

Since it is experiencing a constant torque and constant angular acceleration, the angular displacement can be calculated using:
The angular acceleration is easily calculated using the angular velocity and the time:
Using this value, we can find the angular displacement:
Convert the angular displacement to revolutions by diving by 
← Didn't Know|Knew It →
A circular disk of radius 0.5m and mass 3kg has a force of 25N exerted perpendicular to its edge, causing it to spin. What is the angular acceleration of the disk?
A circular disk of radius 0.5m and mass 3kg has a force of 25N exerted perpendicular to its edge, causing it to spin. What is the angular acceleration of the disk?
Tap to reveal answer
We can find the angular acceleration using the rotaional motion equivalent of Newton's second law. In rotational motion, torque is the product of moment of inertia and angular acceleration:

The moment of inertia for a circular disk is:

The tourque is the product of force and distance (in this case, the radius):

We can plug these into our first equation:

Simplify and rearrange to derive an equation for angular acceleration:

Use our given values to solve:

We can find the angular acceleration using the rotaional motion equivalent of Newton's second law. In rotational motion, torque is the product of moment of inertia and angular acceleration:
The moment of inertia for a circular disk is:
The tourque is the product of force and distance (in this case, the radius):
We can plug these into our first equation:
Simplify and rearrange to derive an equation for angular acceleration:
Use our given values to solve:
← Didn't Know|Knew It →
A 0.18 m long wrench is used to turn the nut on the end of a bolt. A force of 85 N is applied downward to the end of the wrench, as shown in the figure. The angle between the force and the handle of the wrench is 65 degrees.

What is the magnitude and direction of the torque (around the center of the bolt) due to this force?
A 0.18 m long wrench is used to turn the nut on the end of a bolt. A force of 85 N is applied downward to the end of the wrench, as shown in the figure. The angle between the force and the handle of the wrench is 65 degrees.

What is the magnitude and direction of the torque (around the center of the bolt) due to this force?
Tap to reveal answer
To calculate the magnitude of the torque,

where the radius  is the distance between the center of rotation and the location of the force
is the distance between the center of rotation and the location of the force  and the angle
and the angle  is between the radius
is between the radius  and the force
and the force  .
.
The magnitude is thus,

The direction of torque is perpendicular to the plane of the radius  and the force
and the force  , and is given by Right Hand Rule by crossing the radius vector into the force vector. For this situation, the radius vector is left and downward and the force is downward, resulting in the direction of the torque out of the page.
, and is given by Right Hand Rule by crossing the radius vector into the force vector. For this situation, the radius vector is left and downward and the force is downward, resulting in the direction of the torque out of the page.
To calculate the magnitude of the torque,
where the radius 




The magnitude is thus,
The direction of torque is perpendicular to the plane of the radius 

← Didn't Know|Knew It →
A meter stick is nailed to a table at one end and is free to rotate in a horizontal plane parallel to the top of the table. Four forces of equal magnitude are applied to the meter stick at different locations. The figure below shows the view of the meter stick from above.
You may assume the forces  and
and  are applied at the center of the meter stick, and the forces
are applied at the center of the meter stick, and the forces  and
and  are applied at the end opposite the nail.
are applied at the end opposite the nail.

What is the relationship among the magnitudes of the torques on the meter stick caused by the four different forces?
A meter stick is nailed to a table at one end and is free to rotate in a horizontal plane parallel to the top of the table. Four forces of equal magnitude are applied to the meter stick at different locations. The figure below shows the view of the meter stick from above.
You may assume the forces 




What is the relationship among the magnitudes of the torques on the meter stick caused by the four different forces?
Tap to reveal answer
Torque is given by,

Since all of the forces are equal in magnitude, the magnitude of the torque is then influenced by the radius r and the angle theta between the radius and the force.
For  ,
,

For  ,
,

For  ,
,

For  ,
,

Combining this information yields the relationship,

Torque is given by,
Since all of the forces are equal in magnitude, the magnitude of the torque is then influenced by the radius r and the angle theta between the radius and the force.
For 
For 
For 
For 
Combining this information yields the relationship,
← Didn't Know|Knew It →
A man sits on the end of a long uniform metal beam of length  . The man has a mass of
. The man has a mass of  and the beam has a mass of
and the beam has a mass of  .
.
What is the magnitude of the net torque on the plank about the secured end of the beam? Use gravity  .
.
A man sits on the end of a long uniform metal beam of length 


What is the magnitude of the net torque on the plank about the secured end of the beam? Use gravity 
Tap to reveal answer
The net torque on the beam is given by addition of the torques caused by the weight of the man and the weight of the beam itself, each at its respective distance from the end of the beam:

Let's assign the direction of positive torque in the direction of the torques of the man's and the beam's weights, noting that they will add together since they both point in the same direction.


We can further simplify by combining like terms:

Using the given numerical values,

The net torque on the beam is given by addition of the torques caused by the weight of the man and the weight of the beam itself, each at its respective distance from the end of the beam:
Let's assign the direction of positive torque in the direction of the torques of the man's and the beam's weights, noting that they will add together since they both point in the same direction.
We can further simplify by combining like terms:
Using the given numerical values,
← Didn't Know|Knew It →
Two children sit on the opposite sides of a seasaw at a playground, doing so in a way that causes the seasaw to balance perfectly horizontal. The  child on the left is
child on the left is  from the pivot.
from the pivot.
What is the mass of the second child if she sits  from the pivot?
from the pivot?
Two children sit on the opposite sides of a seasaw at a playground, doing so in a way that causes the seasaw to balance perfectly horizontal. The 

What is the mass of the second child if she sits 
Tap to reveal answer
A torque analysis is appropriate in this situation due to the inclusion of distances from a given pivot point. Generally,

This is a static situation. There are two torques about the pivot caused by the weights of two children. We will note that these weights cause torques in opposite directions about the pivot, such that

Consequently,


Or more simply,

Solving for  ,
,

A torque analysis is appropriate in this situation due to the inclusion of distances from a given pivot point. Generally,
This is a static situation. There are two torques about the pivot caused by the weights of two children. We will note that these weights cause torques in opposite directions about the pivot, such that
Consequently,
Or more simply,
Solving for 
← Didn't Know|Knew It →
A gymnast is practicing her balances on a long narrow plank supported at both ends. Her mass is  . The
. The  long plank has a mass of
long plank has a mass of  .
.

Calculate the force the right support provides upward if she stands  from the right end. Use gravity
from the right end. Use gravity  .
.
A gymnast is practicing her balances on a long narrow plank supported at both ends. Her mass is 



Calculate the force the right support provides upward if she stands 

Tap to reveal answer
A torque analysis is appropriate in this situation due to the inclusion of distances from a given pivot point. Generally,

This is a static situation. As such, any pivot point can be chosen about which to do a torque analysis. The quickest way to the unknown force asked for in the question is to do the torque analysis about the left end of the plank. There are three torques about this pivot: two clockwise caused by the weights of the gymnast and the plank itself, and one counterclockwise caused by the force from the right support. Designating clockwise as positive,

Consequently,


This simplifies to

Solving for  ,
,

Solving with numerical values,

A torque analysis is appropriate in this situation due to the inclusion of distances from a given pivot point. Generally,
This is a static situation. As such, any pivot point can be chosen about which to do a torque analysis. The quickest way to the unknown force asked for in the question is to do the torque analysis about the left end of the plank. There are three torques about this pivot: two clockwise caused by the weights of the gymnast and the plank itself, and one counterclockwise caused by the force from the right support. Designating clockwise as positive,
Consequently,
This simplifies to
Solving for 
Solving with numerical values,
← Didn't Know|Knew It →
A square of side lengths  and mass
and mass  is shown with
is shown with  possible axes of rotation.
possible axes of rotation.

Which statement of relationships among the moments of inertia is correct?
A square of side lengths 



Which statement of relationships among the moments of inertia is correct?
Tap to reveal answer
The moments of inertia for both axes  and
and  are equal because both of these axes are equivalently passing through the center of the mass.
are equal because both of these axes are equivalently passing through the center of the mass.
By the parallel axis theorem for moments of inertia ( ), the moment of inertia for axis
), the moment of inertia for axis  is larger than
is larger than  or
or 
because it is located a distance
 away from the center of mass.
away from the center of mass.
The moments of inertia for both axes 

By the parallel axis theorem for moments of inertia (


because it is located a distance

← Didn't Know|Knew It →
A wind catcher is created by attaching four plastic bowls of mass  each to the ends of four lightweight rods, which are then secured to a central rod that is free to rotate in the wind. The four lightweight rods are of lengths
each to the ends of four lightweight rods, which are then secured to a central rod that is free to rotate in the wind. The four lightweight rods are of lengths  ,
,  ,
,  , and
, and  .
.

Calculate the moment of inertia of the four bowls about the central rod. You may assume to bowls to be point masses.
A wind catcher is created by attaching four plastic bowls of mass 





Calculate the moment of inertia of the four bowls about the central rod. You may assume to bowls to be point masses.
Tap to reveal answer
The moment of inertia for a point mass is  .
.
To calculate the total moment of inertia, we add the moment of inertia for each part of the object, such that


The masses of the bowls are all equal in this problem, so this simplifies to

Plugging in and solving with numerical values,

The moment of inertia for a point mass is 
To calculate the total moment of inertia, we add the moment of inertia for each part of the object, such that
The masses of the bowls are all equal in this problem, so this simplifies to
Plugging in and solving with numerical values,
← Didn't Know|Knew It →
A long uniform thin rod of length  has a mass of
has a mass of  .
.
Calculate the moment of rotational inertia about an axis perpendicular to its length passing through a point  from one of its ends.
from one of its ends.
A long uniform thin rod of length 

Calculate the moment of rotational inertia about an axis perpendicular to its length passing through a point 
Tap to reveal answer
For a long thin rod about its center of mass,

According to the parallel axis theorem,

where  is defined to be the distance between the center of mass of the object and the location of the axis parallel to one through the center of mass. For this problem,
is defined to be the distance between the center of mass of the object and the location of the axis parallel to one through the center of mass. For this problem,  is the difference between the given distance and half the length of the rod.
is the difference between the given distance and half the length of the rod.
Combining the above,

Inserting numerical values,

For a long thin rod about its center of mass,
According to the parallel axis theorem,
where 

Combining the above,
Inserting numerical values,
← Didn't Know|Knew It →
The moment of inertia of a long thin rod about its end is determined to be  .
.
What is the new value if the mass and length of the rod are both reduced by a factor of  ?
?
The moment of inertia of a long thin rod about its end is determined to be 
What is the new value if the mass and length of the rod are both reduced by a factor of 
Tap to reveal answer
The moment of inertia for a long uniform thin rod about its end is given by

Reducing the mass and the length by a factor of four introduces the following factors into the equation,

Simplifying,

The moment of inertia for a long uniform thin rod about its end is given by
Reducing the mass and the length by a factor of four introduces the following factors into the equation,
Simplifying,
← Didn't Know|Knew It →
An art sculpture comprised of a long hollow painted cylinder is designed to pivot about an axis located along its long edge. The cylinder has mass  , radius
, radius  , and length
, and length  .
.
Calculate the moment of inertia of the sculpture about this axis.
An art sculpture comprised of a long hollow painted cylinder is designed to pivot about an axis located along its long edge. The cylinder has mass 


Calculate the moment of inertia of the sculpture about this axis.
Tap to reveal answer
The moment of inertia for a hollow cylinder about its center is given by

The parallel axis is applied here because the pivot axis is located on the outside edge of the cylinder, a distance  from the center of mass:
from the center of mass:

Incidentally, for this problem, the length does not contribute to the moment of inertia.
The moment of inertia for a hollow cylinder about its center is given by
The parallel axis is applied here because the pivot axis is located on the outside edge of the cylinder, a distance 
Incidentally, for this problem, the length does not contribute to the moment of inertia.
← Didn't Know|Knew It →
A meter stick is nailed to a table at one end and is free to rotate in a horizontal plane parallel to the top of the table. A force of
meter stick is nailed to a table at one end and is free to rotate in a horizontal plane parallel to the top of the table. A force of  is applied perpendicularly to its length at a distance
is applied perpendicularly to its length at a distance  from the nailed end.
from the nailed end.
Calculate the resulting angular acceleration experienced by the meter stick.
A


Calculate the resulting angular acceleration experienced by the meter stick.
Tap to reveal answer
For a net torque applied to an object free to rotate,

The net torque for this problem is supplied by the  force applied at a distance
force applied at a distance  from the pivot. The torque of a force is calculated by
from the pivot. The torque of a force is calculated by

The moment of inertia for a long uniform thin rod about its end is

Combining above,

Solving for the angular acceleration,

For a net torque applied to an object free to rotate,
The net torque for this problem is supplied by the 

The moment of inertia for a long uniform thin rod about its end is
Combining above,
Solving for the angular acceleration,
← Didn't Know|Knew It →
A  meter stick is secured at one end so that it is free to rotate in a vertical circle. It is held perfectly horizontally, and released.
meter stick is secured at one end so that it is free to rotate in a vertical circle. It is held perfectly horizontally, and released.
Calculate the instantaneous angular acceleration the moment it is released.
A 
Calculate the instantaneous angular acceleration the moment it is released.
Tap to reveal answer
For a net torque applied to an object free to rotate,

The net torque for this problem is supplied by the  force applied at a distance
force applied at a distance  from the pivot. The torque of a force is calculated by
from the pivot. The torque of a force is calculated by

The moment of inertia for a long uniform thin rod about its end is

Combining above,

where the force causing the torque is the meter stick's weight, which is applied at the center of mass of the meter stick - a distance of half the length away from its end.
Solving for the angular acceleration,

Solving numerically,

For a net torque applied to an object free to rotate,
The net torque for this problem is supplied by the 

The moment of inertia for a long uniform thin rod about its end is
Combining above,
where the force causing the torque is the meter stick's weight, which is applied at the center of mass of the meter stick - a distance of half the length away from its end.
Solving for the angular acceleration,
Solving numerically,
← Didn't Know|Knew It →
What is the rotational equivalent of mass?
What is the rotational equivalent of mass?
Tap to reveal answer
The correct answer is moment of inertia. For linear equations, mass is what resists force and causes lower linear accelerations. Similarly, in rotational equations, moment of inertia resists torque and causes lower angular accelerations.
The correct answer is moment of inertia. For linear equations, mass is what resists force and causes lower linear accelerations. Similarly, in rotational equations, moment of inertia resists torque and causes lower angular accelerations.
← Didn't Know|Knew It →
In rotational kinematics equations, what quantity is analogous to force in linear kinematics equations?
In rotational kinematics equations, what quantity is analogous to force in linear kinematics equations?
Tap to reveal answer
Just as force causes linear acceleration, torque causes angular acceleration. This can be seen most in the linear-rotational comparison of Newton's second law:


Just as force causes linear acceleration, torque causes angular acceleration. This can be seen most in the linear-rotational comparison of Newton's second law:
← Didn't Know|Knew It →
A boot is put in a  stick which is attached to a rotor. The rotor turns with an angular velocity of
stick which is attached to a rotor. The rotor turns with an angular velocity of  . What is the linear velocity of the boot?
. What is the linear velocity of the boot?
A boot is put in a 

Tap to reveal answer
Linear (tangential) velocity,  is given by the following equation:
is given by the following equation:

Here,  is the angular velocity in radians per second and
is the angular velocity in radians per second and  is the radius in meters.
is the radius in meters.

Solve.


Linear (tangential) velocity, 
Here, 

Solve.
← Didn't Know|Knew It →

A particle is moving at constant speed in a straight line past a fixed point in space, c. How does the angular momentum of the particle about the fixed point in space change as the particle moves from point a to point b?

A particle is moving at constant speed in a straight line past a fixed point in space, c. How does the angular momentum of the particle about the fixed point in space change as the particle moves from point a to point b?
Tap to reveal answer
The angular momentum of a particle about a fixed axis is  . As the particle draws nearer the fixed axis, both
. As the particle draws nearer the fixed axis, both  and
and  change. However, the product
change. However, the product  remains constant. If you imagine a triangle connecting the three points, the product
remains constant. If you imagine a triangle connecting the three points, the product  represents the
represents the  "of closest approach", labeled "
"of closest approach", labeled " " in the diagram.
" in the diagram.

The angular momentum of a particle about a fixed axis is 







← Didn't Know|Knew It →
Two solid cylinderical disks have equal radii. The first disk is spinning clockwise at  and the second disk is spinning counterclockwise at
and the second disk is spinning counterclockwise at  . The second disk has a mass three times larger than the first. If both spinning disks are combined to form one disk, they end up rotating at the same angular velocity and same direction. Find this angular velocity after combination.
. The second disk has a mass three times larger than the first. If both spinning disks are combined to form one disk, they end up rotating at the same angular velocity and same direction. Find this angular velocity after combination.
Two solid cylinderical disks have equal radii. The first disk is spinning clockwise at 

Tap to reveal answer
For the first disk, we have the information below.

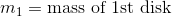


For the second disk, we have the information below.

(The minus sign indicates counterclockwise while the positive indicates clockwise.)



To do this problem, we use conservation of angular momentum. Before the disks are put in contact, the initial total angular momentum is given by the equation below.

It is just the sum of the angular momentums of each disk. When the disks are combined together, then final angular momentum can be found by the following equation.

Set this equal to the initial angular momentum.

Simplify and solve for  .
.

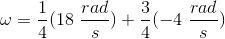

For the first disk, we have the information below.
For the second disk, we have the information below.
(The minus sign indicates counterclockwise while the positive indicates clockwise.)
To do this problem, we use conservation of angular momentum. Before the disks are put in contact, the initial total angular momentum is given by the equation below.
It is just the sum of the angular momentums of each disk. When the disks are combined together, then final angular momentum can be found by the following equation.
Set this equal to the initial angular momentum.
Simplify and solve for 
← Didn't Know|Knew It →
A piece of space debris is travelling in an elliptical orbit around a planet. At its closest point to the planet, the debris is travelling at  . When the debris is
. When the debris is  from the planet, it travels at
from the planet, it travels at  . How close does the debris get to the planet in its orbit?
. How close does the debris get to the planet in its orbit?
A piece of space debris is travelling in an elliptical orbit around a planet. At its closest point to the planet, the debris is travelling at 


Tap to reveal answer
The equation for conservation of angular momentum is:

This means that the angular momentum of the object at the two points in its orbit must be the same. Since the mass of the debris does not change, this gives us an equality of the product of the velocity and distance of the debris at any two points of its orbit:

Plug in known values.
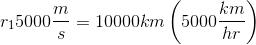
There is disagreement between units; the velocities are given in both  and
and  . Glance down at the answer choices and note that they are all lengths in kilometers.
. Glance down at the answer choices and note that they are all lengths in kilometers.


Solve for  :
:

The equation for conservation of angular momentum is:
This means that the angular momentum of the object at the two points in its orbit must be the same. Since the mass of the debris does not change, this gives us an equality of the product of the velocity and distance of the debris at any two points of its orbit:
Plug in known values.
There is disagreement between units; the velocities are given in both 

Solve for 
← Didn't Know|Knew It →