Harmonic Motion - AP Physics C: Electricity and Magnetism
Card 0 of 220

A block of mass  is attached to two springs, each of whose spring constant is
is attached to two springs, each of whose spring constant is 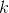 . The ends of the springs are fixed, and the block is free to move back and forth. It is released from rest at an initial amplitude, and its period is measured to be
. The ends of the springs are fixed, and the block is free to move back and forth. It is released from rest at an initial amplitude, and its period is measured to be  . What would the period be if the spring on the right side were to be moved to the other side, attached along side of the other spring?
. What would the period be if the spring on the right side were to be moved to the other side, attached along side of the other spring?

A block of mass 
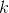

Because the springs are effectively in a parallel arrangement already, moving one does not change the effective spring constant, and therefore does not affect the period.
Because the springs are effectively in a parallel arrangement already, moving one does not change the effective spring constant, and therefore does not affect the period.
Compare your answer with the correct one above
A 5.0 kg mass oscillates once. The total distance it travels is 1.5 m and it takes 4.0 s to travel that distance. What is its frequency of oscillation?
A 5.0 kg mass oscillates once. The total distance it travels is 1.5 m and it takes 4.0 s to travel that distance. What is its frequency of oscillation?
Frequency is only based on the period of the oscillation; all the other given information is useless for this problem. Using  , we can calculate that the frequency is 0.25 Hz.
, we can calculate that the frequency is 0.25 Hz.
Frequency is only based on the period of the oscillation; all the other given information is useless for this problem. Using 
Compare your answer with the correct one above
A mass is attached to a spring, which is fixed to a wall. The mass is pulled away from the spring's equilibrium point and is then released. At what point does the mass experience its maximum kinetic energy?
A mass is attached to a spring, which is fixed to a wall. The mass is pulled away from the spring's equilibrium point and is then released. At what point does the mass experience its maximum kinetic energy?
The formula for determining kinetic energy is

So, kinetic energy will be greatest when the mass is moving most quickly. The force of the spring on the mass increases the mass's velocity until the spring’s equilibrium point, where the force of the spring acts against the motion of the mass, slowing it down. The mass is moving fastest at the spring's equilibrium point, so that's where its kinetic energy is greatest.
The formula for determining kinetic energy is
So, kinetic energy will be greatest when the mass is moving most quickly. The force of the spring on the mass increases the mass's velocity until the spring’s equilibrium point, where the force of the spring acts against the motion of the mass, slowing it down. The mass is moving fastest at the spring's equilibrium point, so that's where its kinetic energy is greatest.
Compare your answer with the correct one above
A mass oscillates on a spring with period  . If the mass is doubled, what is the new period of oscillation?
. If the mass is doubled, what is the new period of oscillation?
A mass oscillates on a spring with period 
The formula for the period of oscillation is
 .
.
When we double the mass, we get:

Because the new factor of 2 is under the square root sign, and also in the numerator, the new period will be increased by  .
.
The formula for the period of oscillation is

When we double the mass, we get:
Because the new factor of 2 is under the square root sign, and also in the numerator, the new period will be increased by 
Compare your answer with the correct one above
A mass is attached to a spring with a spring constant of  . The mass is moved 2 m from the spring's equilibrium point. What is the total energy of the system?
. The mass is moved 2 m from the spring's equilibrium point. What is the total energy of the system?
A mass is attached to a spring with a spring constant of 
The total energy of the system is

but due to the face that the mass currently has no velocity, the kinetic energy term goes to zero.

Plugging in the given values, we can solve for the total energy of the system:


The total energy of the system is
but due to the face that the mass currently has no velocity, the kinetic energy term goes to zero.
Plugging in the given values, we can solve for the total energy of the system:
Compare your answer with the correct one above
A mass is attached to the ceiling by a spring and hangs vertically downward. The mass is stretched downward so its amplitude is  units from its equilibrium position. What is the distance the mass travels during one full oscillation?
units from its equilibrium position. What is the distance the mass travels during one full oscillation?
A mass is attached to the ceiling by a spring and hangs vertically downward. The mass is stretched downward so its amplitude is 
When the mass is at point  , it hasn't traveled at all. When it reaches the spring's equilibrium point, it has traveled a distance of
, it hasn't traveled at all. When it reaches the spring's equilibrium point, it has traveled a distance of  . The mass then continues to a point that's equal to the initial distance traveled, but on the opposite side of the equilibrium point, so the total distance traveled so far is
. The mass then continues to a point that's equal to the initial distance traveled, but on the opposite side of the equilibrium point, so the total distance traveled so far is  . The mass must then travel back to the starting point to complete the oscillation, so the total distance traveled is
. The mass must then travel back to the starting point to complete the oscillation, so the total distance traveled is  .
.
When the mass is at point 



Compare your answer with the correct one above
A simple pendulum of length  swings at a radius
swings at a radius  from a fixed point on the ceiling. As it moves, the pendulum creates an angle
from a fixed point on the ceiling. As it moves, the pendulum creates an angle  with the line that extends vertically downwards from the fixed point. At what angle does the mass attached to the pendulum have the highest kinetic energy?
with the line that extends vertically downwards from the fixed point. At what angle does the mass attached to the pendulum have the highest kinetic energy?
A simple pendulum of length 


The correct answer is  . Since the pendulum is at the bottom of its motion at this point, it has the lowest amount of energy given to gravitational potential and thus, the highest kinetic energy.
. Since the pendulum is at the bottom of its motion at this point, it has the lowest amount of energy given to gravitational potential and thus, the highest kinetic energy.
The correct answer is 
Compare your answer with the correct one above
If a simple pendulum is constructed using a  rope of negligible weight and a large steel ball weighing
rope of negligible weight and a large steel ball weighing  . What is the period of the pendulum?
. What is the period of the pendulum?
If a simple pendulum is constructed using a 

Use the equation for the period of a simple pendulum:
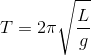
Here, 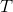 is the period in seconds,
is the period in seconds, 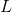 is the length of the pendulum in meters, and
is the length of the pendulum in meters, and 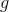 is the acceleration due to gravity in
is the acceleration due to gravity in  .
.
We can plug in the given quantities for length and acceleration to solve for the period.

Note that the mass of the rope as negligible. We also need not incorporate the extraneous information regarding the weight of the steel ball attached to the pendulum. This does not influence the period of this simple pendulum.
Use the equation for the period of a simple pendulum:
Here, 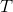
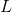
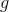

We can plug in the given quantities for length and acceleration to solve for the period.
Note that the mass of the rope as negligible. We also need not incorporate the extraneous information regarding the weight of the steel ball attached to the pendulum. This does not influence the period of this simple pendulum.
Compare your answer with the correct one above
A mass  is attached to a spring of force constant
is attached to a spring of force constant  . The mass rests on a frictionless surface and oscillates horizontally, with oscillations of amplitude
. The mass rests on a frictionless surface and oscillates horizontally, with oscillations of amplitude  . What is the maximum velocity of this mass in terms of
. What is the maximum velocity of this mass in terms of  ,
,  , and
, and  ?
?
A mass 





Relevant equations:



Write expressions for the initial kinetic and potential energies, if the spring is initially stretched to the maximum amplitude before being released.


Write expressions for the final kinetic and potential energies when the spring crosses the equilibrium point.


Use conservation of energy to equate the initial and final energy sums.

Solve the equation to isolate  .
.



Relevant equations:
Write expressions for the initial kinetic and potential energies, if the spring is initially stretched to the maximum amplitude before being released.
Write expressions for the final kinetic and potential energies when the spring crosses the equilibrium point.
Use conservation of energy to equate the initial and final energy sums.
Solve the equation to isolate 
Compare your answer with the correct one above
A ball is attached to a spring on a frictionless, horizontal plane. If the spring constant is  and the mass of the ball three kilograms, at what angular frequency will the system oscillate?
and the mass of the ball three kilograms, at what angular frequency will the system oscillate?
A ball is attached to a spring on a frictionless, horizontal plane. If the spring constant is 
The units for angular frequency,  , are radians per second.
, are radians per second.
We need to derive the equation for angular frequency using conservation of energy.


Rearrange to solve for the velocity:

The velocity is also the product of angular frequency and the distance of the oscillation:

Use this equation to derive the equation for angular frequency:

Finally, use our given mass and spring constant to solve:

The units for angular frequency, 
We need to derive the equation for angular frequency using conservation of energy.
Rearrange to solve for the velocity:
The velocity is also the product of angular frequency and the distance of the oscillation:
Use this equation to derive the equation for angular frequency:
Finally, use our given mass and spring constant to solve:
Compare your answer with the correct one above
A 1kg ball is attached to a massless spring on a frictionless, horizontal plane. If at its equilibrium position, the ball is moving at  , how much total energy is in the system?
, how much total energy is in the system?
A 1kg ball is attached to a massless spring on a frictionless, horizontal plane. If at its equilibrium position, the ball is moving at 
At the equilibrium position, the spring does not contribute any potential energy. It is neither stretched, nor compressed.

All of the energy in the system is kinetic energy, resulting from the given velocity:


At the equilibrium position, the spring does not contribute any potential energy. It is neither stretched, nor compressed.
All of the energy in the system is kinetic energy, resulting from the given velocity:
Compare your answer with the correct one above
A 500g ball is attached to a massless spring on a frictionless, horizontal plane. If at its equilibrium position, the ball is moving at  , and the spring constant is
, and the spring constant is  , what is the maximum displacement of the ball from its equilibrium position?
, what is the maximum displacement of the ball from its equilibrium position?
A 500g ball is attached to a massless spring on a frictionless, horizontal plane. If at its equilibrium position, the ball is moving at 

To solve this question, we will need to use conservation of energy. With no displacement, the ball has a velocity of  and zero displacement. At its maximum displacement, the velocity will be zero and all the energy will be converted to spring potential energy.
and zero displacement. At its maximum displacement, the velocity will be zero and all the energy will be converted to spring potential energy.




Use our given values to solve:


To solve this question, we will need to use conservation of energy. With no displacement, the ball has a velocity of 
Use our given values to solve:
Compare your answer with the correct one above
A bungee-jumping company operates on a bridge 200 m above the ground. They use bungee cords that are 100 m when they are unstretched; these bungee cords have a spring constant of  . What could the mass of their largest customer be before hitting the ground becomes an issue?
. What could the mass of their largest customer be before hitting the ground becomes an issue?

A bungee-jumping company operates on a bridge 200 m above the ground. They use bungee cords that are 100 m when they are unstretched; these bungee cords have a spring constant of 
When a mass is in free fall, its potential energy  is increasing. In this instance, all of that energy must be counteracted by the bungee cord, which we can treat like a spring
is increasing. In this instance, all of that energy must be counteracted by the bungee cord, which we can treat like a spring  , for the person to come to a stop. This means that we can set these two equations as equal to one another:
, for the person to come to a stop. This means that we can set these two equations as equal to one another:

We can then rearrange this equation to solve for  , the mass at which the bungee cord can be stretched as far as the ground:
, the mass at which the bungee cord can be stretched as far as the ground:

Substituting in the known values, we can solve for  :
:


When a mass is in free fall, its potential energy 

We can then rearrange this equation to solve for 
Substituting in the known values, we can solve for 
Compare your answer with the correct one above
An 85 kg stuntman stands on a spring-loaded platform for a movie scene. The spring constant for the platform is  . How far should the platform be compressed to launch the stuntman 7.0 m in the air?
. How far should the platform be compressed to launch the stuntman 7.0 m in the air?
An 85 kg stuntman stands on a spring-loaded platform for a movie scene. The spring constant for the platform is 
All the energy that is stored up by the compressed spring needs to turn into gravitational potential energy for the stuntman to come to a rest 7.0 m in the air. Gravitational potential energy is modeled by the equation  and the energy in the spring system is modeled by the equation
and the energy in the spring system is modeled by the equation  . We can thus set these equations equal to one another:
. We can thus set these equations equal to one another:

We then rearrange the resulting equation for the compressed distance, which is  :
:

Substituting in the given values, we can solve for  :
:


All the energy that is stored up by the compressed spring needs to turn into gravitational potential energy for the stuntman to come to a rest 7.0 m in the air. Gravitational potential energy is modeled by the equation 

We then rearrange the resulting equation for the compressed distance, which is 
Substituting in the given values, we can solve for 
Compare your answer with the correct one above
A mass on the end of a spring oscillates back and forth. The period of an oscillating spring is measured to be 2.27 seconds. The mass is measured to be 0.300 kg. What is the spring's spring constant?
A mass on the end of a spring oscillates back and forth. The period of an oscillating spring is measured to be 2.27 seconds. The mass is measured to be 0.300 kg. What is the spring's spring constant?
To solve this problem, we can use the following equation:

Here,  is the period of an oscillation,
is the period of an oscillation,  is the mass of the oscillating thing in kg, and
is the mass of the oscillating thing in kg, and  is the spring constant in
is the spring constant in  .
.
Rearranging the equation to solve for the spring constant,  , we get:
, we get:

Plugging in the two known values, we get:

Solving for  , we get
, we get  .
.
To solve this problem, we can use the following equation:
Here, 



Rearranging the equation to solve for the spring constant, 
Plugging in the two known values, we get:
Solving for 

Compare your answer with the correct one above
A spring with spring constant  is attached to a 3.0 kg mass. The mass is then displaced 5 cm and released. How long will it take for the mass to travel to a point that's 3.0 cm past the spring’s equilibrium point during its first oscillation?
is attached to a 3.0 kg mass. The mass is then displaced 5 cm and released. How long will it take for the mass to travel to a point that's 3.0 cm past the spring’s equilibrium point during its first oscillation?
A spring with spring constant 
We start with  , where
, where  is the point the mass is traveling to,
is the point the mass is traveling to,  is the maximum displacement,
is the maximum displacement,  is
is  , and
, and  is the time it takes to travel the distance.
is the time it takes to travel the distance.
Rearranging this equation for  gives
gives

Here,  is
is  because the point we're looking for is on the other side of the equilibrium point.
because the point we're looking for is on the other side of the equilibrium point.
We start with 





Rearranging this equation for 
Here, 

Compare your answer with the correct one above
A 10 kg mass is attached to a vertical spring that is hanging from a ceiling. The spring's constant is  . How much will gravity stretch the spring?
. How much will gravity stretch the spring?

A 10 kg mass is attached to a vertical spring that is hanging from a ceiling. The spring's constant is 
We compare the force from Hooke's Law to the force from gravity and solve for displacement:

Rearranging this equation to solve for  , we get
, we get

Plugging in the given values, we get

Solving for  , we get
, we get

We compare the force from Hooke's Law to the force from gravity and solve for displacement:
Rearranging this equation to solve for 
Plugging in the given values, we get
Solving for 
Compare your answer with the correct one above
A 3 kg mass is attached to a spring that is attached to a wall. The mass is pulled 10 cm away from the spring's equilibrium point and released. If the spring has a constant of  , what is the maximum velocity the mass will reach?
, what is the maximum velocity the mass will reach?
A 3 kg mass is attached to a spring that is attached to a wall. The mass is pulled 10 cm away from the spring's equilibrium point and released. If the spring has a constant of 
When the spring is at its maximum compression, its potential energy is maximized and its kinetic energy is 0. When the mass is at the spring's equilibrium point, all of the potential energy is converted into kinetic energy, so kinetic energy is maximized (and equal to the maximum potential energy) and potential energy is 0. We set these two equations equal to each other and solve for velocity.





When the spring is at its maximum compression, its potential energy is maximized and its kinetic energy is 0. When the mass is at the spring's equilibrium point, all of the potential energy is converted into kinetic energy, so kinetic energy is maximized (and equal to the maximum potential energy) and potential energy is 0. We set these two equations equal to each other and solve for velocity.
Compare your answer with the correct one above
All angles in this problem are expressed in radians.
An object oscillates horizontally, and its displacement from equilibrium can be found using the equation:

where  is in seconds. What is the velocity of the object at
is in seconds. What is the velocity of the object at  ?
?
All angles in this problem are expressed in radians.
An object oscillates horizontally, and its displacement from equilibrium can be found using the equation:
where 

To find the equation for velocity, we take the first derivative of the position function. Don't forget the chain rule for the inside of the cosine!




To find the equation for velocity, we take the first derivative of the position function. Don't forget the chain rule for the inside of the cosine!
Compare your answer with the correct one above
A  block on a frictionless table is connected to a horizontal spring with constant
block on a frictionless table is connected to a horizontal spring with constant  . If the block is released from rest when the spring is stretched a distance of
. If the block is released from rest when the spring is stretched a distance of  ,
,
what is its speed when the spring is compressed a distance of  ?
?
A 


what is its speed when the spring is compressed a distance of 
Assuming this is a frictionless table, we don't have to take the work done by friction into account.
This is a conservation of energy problem. In this problem we have to realize that the potential energy of the spring at  is equal to the kinetic energy of the spring at
is equal to the kinetic energy of the spring at  + the potential energy of the spring at
+ the potential energy of the spring at  .
.
This can be shown in the following equation:

If we solve for  , we get the following equation:
, we get the following equation:

Remember to convert the distances given in centimeters to meters.
If we plug in all the variables, we get 
Assuming this is a frictionless table, we don't have to take the work done by friction into account.
This is a conservation of energy problem. In this problem we have to realize that the potential energy of the spring at 


This can be shown in the following equation:
If we solve for 
Remember to convert the distances given in centimeters to meters.
If we plug in all the variables, we get
Compare your answer with the correct one above

