Linear Motion - AP Physics C: Electricity and Magnetism
Card 1 of 286
A guillotine blade weighing  is accelerated upward into position at a rate of
is accelerated upward into position at a rate of  .
.
What is the the approximate mass of the guillotine blade?
A guillotine blade weighing 

What is the the approximate mass of the guillotine blade?
Tap to reveal answer
The force of gravity on the blade is  , which is the same as
, which is the same as 
This unit relationship comes from Newton's second law.
 is the mathematical expression of Newton's second law. The units for force must be a product of the units for mass and the units for acceleration.
is the mathematical expression of Newton's second law. The units for force must be a product of the units for mass and the units for acceleration.
Solve the expression by plugging in known values.


The force of gravity on the blade is 
This unit relationship comes from Newton's second law.

Solve the expression by plugging in known values.
← Didn't Know|Knew It →
A guillotine blade weighing  is accelerated upward into position at a rate of
is accelerated upward into position at a rate of  .
.
What is the tension on the rope pulling the blade, while it is accelerating into position?
A guillotine blade weighing 

What is the tension on the rope pulling the blade, while it is accelerating into position?
Tap to reveal answer
The tension in the rope is the sum of the forces acting on it. If one considers that the net force on an object must equal the mass of the object times the acceleration of the object, the net force on the object must be the force due to tension from the rope minus the force due to gravity.

Rearrange the equation.

Plug in known values.


The tension in the rope is the sum of the forces acting on it. If one considers that the net force on an object must equal the mass of the object times the acceleration of the object, the net force on the object must be the force due to tension from the rope minus the force due to gravity.
Rearrange the equation.
Plug in known values.
← Didn't Know|Knew It →
An object is moving in two dimensions. Its vertical motion relative to the horizontal motion is described by the equation  . Its motion in the horizontal direction is described by the equation
. Its motion in the horizontal direction is described by the equation  . What is the object's velocity is the
. What is the object's velocity is the  direction in terms of its horizontal position
direction in terms of its horizontal position  ?
?
An object is moving in two dimensions. Its vertical motion relative to the horizontal motion is described by the equation 



Tap to reveal answer
The y velocity is thetime derivative of the  position, and not the
position, and not the  derivative. In order to find it, use the chain rule:
derivative. In order to find it, use the chain rule:


Of course, 
The y velocity is thetime derivative of the 

Of course,
← Didn't Know|Knew It →
Two objects moving in one dimension created the following velocity vs. time graph:

From the graph above, what is true about the two objects at time  ?
?
Two objects moving in one dimension created the following velocity vs. time graph:

From the graph above, what is true about the two objects at time 
Tap to reveal answer
Since this is a graph of velocity and not position, the curves intersect where the velocities match. Since we do not know the starting position, we do not know where the objects are relative to one another.
Since this is a graph of velocity and not position, the curves intersect where the velocities match. Since we do not know the starting position, we do not know where the objects are relative to one another.
← Didn't Know|Knew It →
Two objects moving in one dimension created the following velocity vs. time graph:

From the graph above, which object has traveled a greater distance from its starting position when  ?
?
Two objects moving in one dimension created the following velocity vs. time graph:

From the graph above, which object has traveled a greater distance from its starting position when 
Tap to reveal answer
Since this is a graph of velocity vs. time, its integral is distance travelled. We can estimate the integral by looking at the area under the curves. Since Bbject 1 has a greater area under its velocity curve, it has covered a greater distance. Its velocity is greater that Object 2's for the entire time, so it makes sense that it will travel farther.
Since this is a graph of velocity vs. time, its integral is distance travelled. We can estimate the integral by looking at the area under the curves. Since Bbject 1 has a greater area under its velocity curve, it has covered a greater distance. Its velocity is greater that Object 2's for the entire time, so it makes sense that it will travel farther.
← Didn't Know|Knew It →
Atwood's machine consists of two blocks connected by a string connected over a
pulley as shown. What is the acceleration of the blocks if their masses are  and
and  .
.
Assume the pulley has negligible mass and friction.

Atwood's machine consists of two blocks connected by a string connected over a
pulley as shown. What is the acceleration of the blocks if their masses are 

Assume the pulley has negligible mass and friction.

Tap to reveal answer

From the force diagram above, we can see that tension  is pulling up on both sides of the string and gravity is pulling down on both blocks. With this information we can write 2 force equations:
is pulling up on both sides of the string and gravity is pulling down on both blocks. With this information we can write 2 force equations:


If we add the two equations together, we get:

where 
Solving for  , we get
, we get


From the force diagram above, we can see that tension 
If we add the two equations together, we get:
where
Solving for 
← Didn't Know|Knew It →
A  ball is thrown horizontally from the top of a
ball is thrown horizontally from the top of a 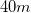 high building. It has an initial velocity of
high building. It has an initial velocity of 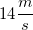 and lands on the ground
and lands on the ground  away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?
away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?
I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
A 
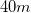
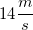

I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
Tap to reveal answer
Relevant equations:


Choice I is true because  is proportional to the range
is proportional to the range  , so increasing
, so increasing  increases
increases  if
if  is constant. This relationship is given by the equation:
is constant. This relationship is given by the equation:

Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon  would be less. Decreasing
would be less. Decreasing 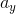 increases the time the ball is in the air, thereby increasing
increases the time the ball is in the air, thereby increasing  if
if  is constant. This relationship is also shown in the equation:
is constant. This relationship is also shown in the equation:

Relevant equations:
Choice I is true because 




Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon 
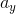


← Didn't Know|Knew It →
Water emerges horizontally from a hole in a tank 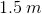 above the ground. If the water hits the ground
above the ground. If the water hits the ground 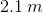 from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)
from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)
Water emerges horizontally from a hole in a tank 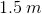
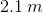
Tap to reveal answer
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation: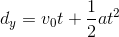
We know that the y-velocity is 0 to start with, acceleration is  and
and  .
.
Substituting into the equation, we get:

Next we have to substitute the time into the equation for the x component

We know that  and
and 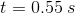 , so we can conclude that:
, so we can conclude that:
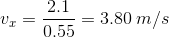
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation:
We know that the y-velocity is 0 to start with, acceleration is 

Substituting into the equation, we get:
Next we have to substitute the time into the equation for the x component
We know that 
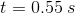
← Didn't Know|Knew It →
An object starts from rest and reaches a velocity of  after accelerating at a constant rate for four seconds. What is the distance traveled in this time?
after accelerating at a constant rate for four seconds. What is the distance traveled in this time?
An object starts from rest and reaches a velocity of 
Tap to reveal answer
Since the acceleration is constant in this problem, we can apply the kinematics given equation to calculate the distance:

First, we need to calculate the acceleration.

Plug in our velocity and time values to find the acceleration.

Now we can return to the kinematics equation and solve for the distance traveled:


Since the acceleration is constant in this problem, we can apply the kinematics given equation to calculate the distance:
First, we need to calculate the acceleration.
Plug in our velocity and time values to find the acceleration.
Now we can return to the kinematics equation and solve for the distance traveled:
← Didn't Know|Knew It →
At the moment a car is passed by another car constantly traveling at  , it begins to accelerate at
, it begins to accelerate at  . In how many seconds does this car catch up to and pass the other car?
. In how many seconds does this car catch up to and pass the other car?
At the moment a car is passed by another car constantly traveling at 

Tap to reveal answer
First, find the displacement equations for both cars. Car 1 will be the car that is initially stationary; car 2 will be the car traveling with constant velocity.
Car 1:



Car 2:


Now, set those displacement equations equal to each other and solve for  .
.



The accelerating car will catch and pass the car traveling at constant velocity after 4 seconds.
First, find the displacement equations for both cars. Car 1 will be the car that is initially stationary; car 2 will be the car traveling with constant velocity.
Car 1:
Car 2:
Now, set those displacement equations equal to each other and solve for 
The accelerating car will catch and pass the car traveling at constant velocity after 4 seconds.
← Didn't Know|Knew It →
An object moving along a line has a displacement equation of  , where
, where  is in seconds. For what value of
is in seconds. For what value of  is the object stationary?
is the object stationary?
An object moving along a line has a displacement equation of 


Tap to reveal answer
Use the fact that  to find the velocity equation, and then solve for
to find the velocity equation, and then solve for  when
when  .
.

Take the derivative of the displacement equation.

Set the velocity equal to zero.

Solve for the time.

Use the fact that 


Take the derivative of the displacement equation.
Set the velocity equal to zero.
Solve for the time.
← Didn't Know|Knew It →
An object is moving on a line and has displacement equation of  , where
, where  is in seconds. At what value of
is in seconds. At what value of  is the object not accelerating?
is the object not accelerating?
An object is moving on a line and has displacement equation of 


Tap to reveal answer
Take the second derivative of  , to find the acceleration function
, to find the acceleration function  . Then find the value of
. Then find the value of  where
where  . The fact that it is simply
. The fact that it is simply  and not
and not  or
or  inside that quantity means that using the Chain Rule becomes decidedly easier.
inside that quantity means that using the Chain Rule becomes decidedly easier.



Set the acceleration fuction equal to zero and solve for the time.


Take the second derivative of 






Set the acceleration fuction equal to zero and solve for the time.
← Didn't Know|Knew It →
A projectile is launched out of a cannon or launch tube with zero air resistance or friction. At what angle (in degrees) should the projectile be launched to maximize the distance it travels?
A projectile is launched out of a cannon or launch tube with zero air resistance or friction. At what angle (in degrees) should the projectile be launched to maximize the distance it travels?
Tap to reveal answer
The projectile travels the farthest when the vertical component of its velocity matches the sum of its horizontal component and whatever the wind/friction adds or subtracts. If the wind has no effect, then a 45-degree angle will be the best because the horizontal and vertical components of the velocity will create a right isosceles triangle (remember special triangles).
The projectile travels the farthest when the vertical component of its velocity matches the sum of its horizontal component and whatever the wind/friction adds or subtracts. If the wind has no effect, then a 45-degree angle will be the best because the horizontal and vertical components of the velocity will create a right isosceles triangle (remember special triangles).
← Didn't Know|Knew It →

A car undergoes acceleration according to the given function. What distance has the car traveled after three seconds?
A car undergoes acceleration according to the given function. What distance has the car traveled after three seconds?
Tap to reveal answer
We can determine the velocity by taking the second integral of acceleration for the time interval of 0s to 3s.


Solve for the first integral.

Solve for the second integral, using the time interval.

We can determine the velocity by taking the second integral of acceleration for the time interval of 0s to 3s.
Solve for the first integral.
Solve for the second integral, using the time interval.
← Didn't Know|Knew It →

A car undergoes acceleration according to the given function. How fast is the car moving after four seconds?
A car undergoes acceleration according to the given function. How fast is the car moving after four seconds?
Tap to reveal answer
We can find the car's velocity by taking the integral of the acceleration function during the given time interval.


Solve the integral for the time interval of 0s to 4s. This will give us the final velocity.

We can find the car's velocity by taking the integral of the acceleration function during the given time interval.
Solve the integral for the time interval of 0s to 4s. This will give us the final velocity.
← Didn't Know|Knew It →

A car undergoes acceleration according to the given function. If the threshold for serious injury or fatality for a human undergoing horizontal acceleration is 60 g ees (1 gee = 10 meters per second per second), how long would a human be able to withstand riding in this car?
A car undergoes acceleration according to the given function. If the threshold for serious injury or fatality for a human undergoing horizontal acceleration is 60 g ees (1 gee = 10 meters per second per second), how long would a human be able to withstand riding in this car?
Tap to reveal answer
Calculate the maximum acceration in meters per second.

Solve for the time.



Calculate the maximum acceration in meters per second.
Solve for the time.
← Didn't Know|Knew It →
A ball travels with a velocity as described by the function below:

What is the ball's acceleration?
A ball travels with a velocity as described by the function below:
What is the ball's acceleration?
Tap to reveal answer
Acceleration is equal to the derivative of the velocity function.

Since the velocity is constant, the derivative will be equal to zero.

The acceleration is equal to zero.
Acceleration is equal to the derivative of the velocity function.
Since the velocity is constant, the derivative will be equal to zero.
The acceleration is equal to zero.
← Didn't Know|Knew It →
A man runs with a velocity described by the function below.

What is the function for his acceleration?
A man runs with a velocity described by the function below.
What is the function for his acceleration?
Tap to reveal answer
The function for acceleration is the derivative of the function for velocity.



The function for acceleration is the derivative of the function for velocity.
← Didn't Know|Knew It →
A man runs with a velocity as described by the function below.

How far does he travel in 1 minute?
A man runs with a velocity as described by the function below.
How far does he travel in 1 minute?
Tap to reveal answer
Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.



Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.
← Didn't Know|Knew It →
A particle traveling in a straight line accelerates uniformly from rest to  in
in  and then continues at constant speed for an additional for an additional
and then continues at constant speed for an additional for an additional  . What is the total distance traveled by the particle during the
. What is the total distance traveled by the particle during the  ?
?
A particle traveling in a straight line accelerates uniformly from rest to 



Tap to reveal answer
First off we have to convert  to meters per second.
to meters per second.

Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be  . The acceleration of the object at this time can be calculated using:
. The acceleration of the object at this time can be calculated using:
 , substituting the values, we get:
, substituting the values, we get:

Next, we use the distance equation to find the distance in the first 5 seconds:

 because the initial speed is
because the initial speed is  .
.
If we plug in  ,
,  , we get:
, we get: 
Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:

 in this case is not equal to
in this case is not equal to  , it is equal to
, it is equal to  and
and 
Plugging in the equation, we get 
Adding  and
and  we get the total distance to be
we get the total distance to be 
First off we have to convert 
Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be 

Next, we use the distance equation to find the distance in the first 5 seconds:


If we plug in 

Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:



Plugging in the equation, we get
Adding 

← Didn't Know|Knew It →