Inference - AP Statistics
Card 1 of 256
A prominent football coach is being reviewed for his performance in the past season. To evaluate how well the coach has done, the team manager runs a statistical test comparing the coach to a sample of coaches in the league. If the test suggests that the coach outperformed other coaches when in fact he did not, and the manager then rejects the null hypothesis (that the coach did not outperform the other coaches), what kind of error is he committing?
A prominent football coach is being reviewed for his performance in the past season. To evaluate how well the coach has done, the team manager runs a statistical test comparing the coach to a sample of coaches in the league. If the test suggests that the coach outperformed other coaches when in fact he did not, and the manager then rejects the null hypothesis (that the coach did not outperform the other coaches), what kind of error is he committing?
Tap to reveal answer
A type I error occurs when one rejects a null hypothesis that is in fact true. The null hypothesis is that the coach does not outperform other coaches, and the test reccomends that we reject it even though it is true. Thus, a type I error has been committed.
A type I error occurs when one rejects a null hypothesis that is in fact true. The null hypothesis is that the coach does not outperform other coaches, and the test reccomends that we reject it even though it is true. Thus, a type I error has been committed.
← Didn't Know|Knew It →
If a hypothesis test uses a  confidence level, then what is its probability of Type I Error?
confidence level, then what is its probability of Type I Error?
If a hypothesis test uses a 
Tap to reveal answer
By definition, the probability of Type I Error is,

where,
 represents Probability of Type I Error and
represents Probability of Type I Error and  represents the confidence level.
represents the confidence level.
Thus resulting in:

By definition, the probability of Type I Error is,
where,


Thus resulting in:
← Didn't Know|Knew It →
For significance tests, which of the following is an incorrect way to increase power (the probability of correctly rejecting the null hypothesis)?
For significance tests, which of the following is an incorrect way to increase power (the probability of correctly rejecting the null hypothesis)?
Tap to reveal answer
Recall that power is  . The probability of Type I and Type II errors will change inversely of each other as the probability of making a Type I error changes. If
. The probability of Type I and Type II errors will change inversely of each other as the probability of making a Type I error changes. If  increases, then
increases, then  decreases, and as a result power will increase. So if
decreases, and as a result power will increase. So if  decreases,
decreases,  would increase, and power would decrease; therefore decreasing
would increase, and power would decrease; therefore decreasing  will not increase power.
will not increase power.
Recall that power is 





← Didn't Know|Knew It →
In a recent athletic study, your lab partner told you that they rejected the null hypothesis that the fabric of running shoes has no effect on the wearer's running times.
If the null hypothesis was actually valid, what type of error was made?
In a recent athletic study, your lab partner told you that they rejected the null hypothesis that the fabric of running shoes has no effect on the wearer's running times.
If the null hypothesis was actually valid, what type of error was made?
Tap to reveal answer
A type I error occurs when the null hypothesis is valid but rejected.
A type II error occurs when the null hypothesis is false, but fails to be rejected.
Because the null hypothesis was true, but rejected, they made a Type I error.
A type I error occurs when the null hypothesis is valid but rejected.
A type II error occurs when the null hypothesis is false, but fails to be rejected.
Because the null hypothesis was true, but rejected, they made a Type I error.
← Didn't Know|Knew It →
In a recent academic study, your lab partner told you that they rejected the null hypothesis that the ionization of water has no effect on the rate of grass growth.
If the null hypothesis was actually valid, what type of error was made?
In a recent academic study, your lab partner told you that they rejected the null hypothesis that the ionization of water has no effect on the rate of grass growth.
If the null hypothesis was actually valid, what type of error was made?
Tap to reveal answer
A type I error occurs when the null hypothesis is valid but rejected.
A type II error occurs when the null hypothesis is false, but fails to be rejected.
Because the null hypothesis was true, but rejected, they made a Type I error.
A type I error occurs when the null hypothesis is valid but rejected.
A type II error occurs when the null hypothesis is false, but fails to be rejected.
Because the null hypothesis was true, but rejected, they made a Type I error.
← Didn't Know|Knew It →
A company claims that they have 12 ounces of potato chips in each of their bags of chips. A customer complaint is filed that they do not truly contain 12 ounces but actually contain less. A sampling test is conducted to see if the comapny measure is true or not. What would be an example of a Type I error?
A company claims that they have 12 ounces of potato chips in each of their bags of chips. A customer complaint is filed that they do not truly contain 12 ounces but actually contain less. A sampling test is conducted to see if the comapny measure is true or not. What would be an example of a Type I error?
Tap to reveal answer
The type I error is rejecting the null hypothesis when it is actually true. The null here is 12 ounces per bag so a type I error would be rejecting the company claim even though there are 12 ounces per bag.
The type I error is rejecting the null hypothesis when it is actually true. The null here is 12 ounces per bag so a type I error would be rejecting the company claim even though there are 12 ounces per bag.
← Didn't Know|Knew It →
What is  , or the expected value of
, or the expected value of  for any distribution?
for any distribution?
What is 

Tap to reveal answer
 is
is  , or the mean, of the population. This makes sense since
, or the mean, of the population. This makes sense since  literally means the expected value of
literally means the expected value of  . The mean is the expected value of
. The mean is the expected value of  .
.





← Didn't Know|Knew It →
Tap to reveal answer
No explanation available
No explanation available
← Didn't Know|Knew It →
You estimate a regression model with  and
and  , where
, where  is the beta coefficient and
is the beta coefficient and  is the standard error. Construct 95% confidence intervals for
is the standard error. Construct 95% confidence intervals for 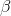 .
.
You estimate a regression model with 



Tap to reveal answer
To construct 95% confidence intervals for  , we simply take the coefficient and add/subtract
, we simply take the coefficient and add/subtract  . This is because
. This is because  is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of
is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of  .
.
To construct 95% confidence intervals for 



← Didn't Know|Knew It →
In a recent academic study, your lab partner told you that they rejected the null hypothesis that the ionization of water has no effect on the rate of grass growth.
If the null hypothesis was actually valid, what type of error was made?
In a recent academic study, your lab partner told you that they rejected the null hypothesis that the ionization of water has no effect on the rate of grass growth.
If the null hypothesis was actually valid, what type of error was made?
Tap to reveal answer
A type I error occurs when the null hypothesis is valid but rejected.
A type II error occurs when the null hypothesis is false, but fails to be rejected.
Because the null hypothesis was true, but rejected, they made a Type I error.
A type I error occurs when the null hypothesis is valid but rejected.
A type II error occurs when the null hypothesis is false, but fails to be rejected.
Because the null hypothesis was true, but rejected, they made a Type I error.
← Didn't Know|Knew It →
A company claims that they have 12 ounces of potato chips in each of their bags of chips. A customer complaint is filed that they do not truly contain 12 ounces but actually contain less. A sampling test is conducted to see if the comapny measure is true or not. What would be an example of a Type I error?
A company claims that they have 12 ounces of potato chips in each of their bags of chips. A customer complaint is filed that they do not truly contain 12 ounces but actually contain less. A sampling test is conducted to see if the comapny measure is true or not. What would be an example of a Type I error?
Tap to reveal answer
The type I error is rejecting the null hypothesis when it is actually true. The null here is 12 ounces per bag so a type I error would be rejecting the company claim even though there are 12 ounces per bag.
The type I error is rejecting the null hypothesis when it is actually true. The null here is 12 ounces per bag so a type I error would be rejecting the company claim even though there are 12 ounces per bag.
← Didn't Know|Knew It →
A prominent football coach is being reviewed for his performance in the past season. To evaluate how well the coach has done, the team manager runs a statistical test comparing the coach to a sample of coaches in the league. If the test suggests that the coach outperformed other coaches when in fact he did not, and the manager then rejects the null hypothesis (that the coach did not outperform the other coaches), what kind of error is he committing?
A prominent football coach is being reviewed for his performance in the past season. To evaluate how well the coach has done, the team manager runs a statistical test comparing the coach to a sample of coaches in the league. If the test suggests that the coach outperformed other coaches when in fact he did not, and the manager then rejects the null hypothesis (that the coach did not outperform the other coaches), what kind of error is he committing?
Tap to reveal answer
A type I error occurs when one rejects a null hypothesis that is in fact true. The null hypothesis is that the coach does not outperform other coaches, and the test reccomends that we reject it even though it is true. Thus, a type I error has been committed.
A type I error occurs when one rejects a null hypothesis that is in fact true. The null hypothesis is that the coach does not outperform other coaches, and the test reccomends that we reject it even though it is true. Thus, a type I error has been committed.
← Didn't Know|Knew It →
If a hypothesis test uses a  confidence level, then what is its probability of Type I Error?
confidence level, then what is its probability of Type I Error?
If a hypothesis test uses a 
Tap to reveal answer
By definition, the probability of Type I Error is,

where,
 represents Probability of Type I Error and
represents Probability of Type I Error and  represents the confidence level.
represents the confidence level.
Thus resulting in:

By definition, the probability of Type I Error is,
where,


Thus resulting in:
← Didn't Know|Knew It →
For significance tests, which of the following is an incorrect way to increase power (the probability of correctly rejecting the null hypothesis)?
For significance tests, which of the following is an incorrect way to increase power (the probability of correctly rejecting the null hypothesis)?
Tap to reveal answer
Recall that power is  . The probability of Type I and Type II errors will change inversely of each other as the probability of making a Type I error changes. If
. The probability of Type I and Type II errors will change inversely of each other as the probability of making a Type I error changes. If  increases, then
increases, then  decreases, and as a result power will increase. So if
decreases, and as a result power will increase. So if  decreases,
decreases,  would increase, and power would decrease; therefore decreasing
would increase, and power would decrease; therefore decreasing  will not increase power.
will not increase power.
Recall that power is 





← Didn't Know|Knew It →
In a recent athletic study, your lab partner told you that they rejected the null hypothesis that the fabric of running shoes has no effect on the wearer's running times.
If the null hypothesis was actually valid, what type of error was made?
In a recent athletic study, your lab partner told you that they rejected the null hypothesis that the fabric of running shoes has no effect on the wearer's running times.
If the null hypothesis was actually valid, what type of error was made?
Tap to reveal answer
A type I error occurs when the null hypothesis is valid but rejected.
A type II error occurs when the null hypothesis is false, but fails to be rejected.
Because the null hypothesis was true, but rejected, they made a Type I error.
A type I error occurs when the null hypothesis is valid but rejected.
A type II error occurs when the null hypothesis is false, but fails to be rejected.
Because the null hypothesis was true, but rejected, they made a Type I error.
← Didn't Know|Knew It →
Tap to reveal answer
No explanation available
No explanation available
← Didn't Know|Knew It →
Tap to reveal answer
No explanation available
No explanation available
← Didn't Know|Knew It →
Tap to reveal answer
No explanation available
No explanation available
← Didn't Know|Knew It →
In a simple random sample of 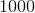 people,
people,  are left-handed. Find a
are left-handed. Find a  confidence interval for the true proportion of left-handed people in the entire population.
confidence interval for the true proportion of left-handed people in the entire population.
In a simple random sample of 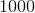


Tap to reveal answer
Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is

Step 2:  , or the sample proportion is equal to
, or the sample proportion is equal to 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within  .
.

Step 4: Substitue all the values into the equation to get the answer.

Step 1: Determine the approporiate formula. In this case, the statistic is a proportion because the question says 261 people out of 1000 are left-handed. We want to use a confidence interval for proportions. The equation is
Step 2: 
Step 3: The questions asks for a 95% confidence interval. You can assume a normal distribution because of the large sample size. Therefore, in a normal distribution, 95% of the data is contained within 
Step 4: Substitue all the values into the equation to get the answer.
← Didn't Know|Knew It →
What is  , or the expected value of
, or the expected value of  for any distribution?
for any distribution?
What is 

Tap to reveal answer
 is
is  , or the mean, of the population. This makes sense since
, or the mean, of the population. This makes sense since  literally means the expected value of
literally means the expected value of  . The mean is the expected value of
. The mean is the expected value of  .
.





← Didn't Know|Knew It →