Random Variables - AP Statistics
Card 1 of 88
Which of the following is NOT a discrete random variable?
Which of the following is NOT a discrete random variable?
Tap to reveal answer
By definition, a discrete random variable is a random variable whose values can be "counted" one by one. A continuous random variable is a random variable that can take any value on a certain interval. Of these choices, the number of lip products, the amount of money, and the number of midterms taken are all discrete random variables, as the respective values can be counted; however, the time taken to watch the first four seasons of a TV show is a continuous random variable, as not everyone will take the same amount of time to watch all those episodes (i.e. some might fastf-orward/replay parts of episodes).
By definition, a discrete random variable is a random variable whose values can be "counted" one by one. A continuous random variable is a random variable that can take any value on a certain interval. Of these choices, the number of lip products, the amount of money, and the number of midterms taken are all discrete random variables, as the respective values can be counted; however, the time taken to watch the first four seasons of a TV show is a continuous random variable, as not everyone will take the same amount of time to watch all those episodes (i.e. some might fastf-orward/replay parts of episodes).
← Didn't Know|Knew It →
Police estimate that 85% of drivers do not text and drive. They set up a safety roadblock at a busy intersection to check for this infraction.
What is the probability that the first texter is in the thirteenth car stopped?
Police estimate that 85% of drivers do not text and drive. They set up a safety roadblock at a busy intersection to check for this infraction.
What is the probability that the first texter is in the thirteenth car stopped?
Tap to reveal answer
This question pertains to the concept of Geometric Probability Distribution, which states that the probability of 
trials until the first success is as follows:
In this equation, 
is the probability of success (in this case, a driver caught texting), and 
is the probability of failure.
In this particular problem, 
, and 
. To calculate the probability of finding that the first driver caught texting is in the thirteenth car stopped, we can calculate 
. The final answer is 
.
This question pertains to the concept of Geometric Probability Distribution, which states that the probability of
In this equation,
In this particular problem,
← Didn't Know|Knew It →
Variable 
has a Poisson distribution with a mean of 
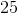. What is the variance of Variable 
?
Variable
Tap to reveal answer
Because 
has a Poisson distribution we know that:
and
.
Therefore, since we are given the mean of 25, we can find its variance to also be 25.
Because
Therefore, since we are given the mean of 25, we can find its variance to also be 25.
← Didn't Know|Knew It →
Tap to reveal answer
No explanation available
No explanation available
← Didn't Know|Knew It →
Tap to reveal answer
No explanation available
No explanation available
← Didn't Know|Knew It →
Let us suppose you are a waiter. You work your first four shifts and receive the following in tips: (1) 20, (2) 30, (3) 15, (4) 5. What is the mean amount of tips you will receive in a given day?
Let us suppose you are a waiter. You work your first four shifts and receive the following in tips: (1) 20, (2) 30, (3) 15, (4) 5. What is the mean amount of tips you will receive in a given day?
Tap to reveal answer
The answer is 17.5. Simply take the values for each day, add them, and divide by the total number of days to obtain the mean: 
The answer is 17.5. Simply take the values for each day, add them, and divide by the total number of days to obtain the mean:
← Didn't Know|Knew It →
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the mean outcome for the number of hours that Robert will work?
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the mean outcome for the number of hours that Robert will work?
Tap to reveal answer
We are required to find the mean outcome where the probability of each possible result varies--the random/weighted mean. First, multiply each possible outcome by the probability of that outcome occurring. Second, add these results together.
We are required to find the mean outcome where the probability of each possible result varies--the random/weighted mean. First, multiply each possible outcome by the probability of that outcome occurring. Second, add these results together.
← Didn't Know|Knew It →
There are 
collectable coins in a bag. 
are 
ounces, 
are 
ounces, 
are 
ounces, and 
are 
ounces. If one coin is randomly selected, what is the mean possible weight in ounces?
There are
Tap to reveal answer
We are required to find the mean outcome where the probability of each possible result varies--the random/weighted mean.
First, multiply each possible outcome by the probability of that outcome occurring.
Second, add these results together.
We are required to find the mean outcome where the probability of each possible result varies--the random/weighted mean.
First, multiply each possible outcome by the probability of that outcome occurring.
Second, add these results together.
← Didn't Know|Knew It →
A basketball player makes 
of his three-point shots. If he takes 
three-point shots each game, how many points per game does he score from three-point range?
A basketball player makes
Tap to reveal answer
First convert 
.
The player's three-point shooting follows a binomial distribution with 
and 
.
On average, he thus makes 
three-point shots per game.
This means he averages 12 points per game from three-point range if he tries to make 10 three-pointers per game.
First convert
The player's three-point shooting follows a binomial distribution with
On average, he thus makes
This means he averages 12 points per game from three-point range if he tries to make 10 three-pointers per game.
← Didn't Know|Knew It →
Tim samples the average plant height of potato plants for his science class and finds the following distribution (in inches):
Which of the following is/are true about the data?
i: the mode is 
ii: the mean is 
iii: the median is 
iv: the range is 
Tim samples the average plant height of potato plants for his science class and finds the following distribution (in inches):
Which of the following is/are true about the data?
i: the mode is
ii: the mean is
iii: the median is
iv: the range is
Tap to reveal answer
Analyzing the data, there are more 6s than anything else (mode), the median is between 
and 
, the mean is 
, and the range is 
Analyzing the data, there are more 6s than anything else (mode), the median is between
← Didn't Know|Knew It →
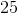Variable has a Poisson distribution with a mean of . What is the variance of Variable ?
Variable
Tap to reveal answer
Because has a Poisson distribution we know that:
and
.
Therefore, since we are given the mean of 25, we can find its variance to also be 25.
Because
Therefore, since we are given the mean of 25, we can find its variance to also be 25.
← Didn't Know|Knew It →
Tap to reveal answer
No explanation available
No explanation available
← Didn't Know|Knew It →
Tap to reveal answer
No explanation available
No explanation available
← Didn't Know|Knew It →
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the standard deviation of the possible outcomes?
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the standard deviation of the possible outcomes?
Tap to reveal answer
There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. Second, for each value in the group (45, 40, 25, and 12), subtract the mean from each and multiply the result by the probability of that outcome occurring. Third, add the four results together. Fourth, find the square root of the result.
There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. Second, for each value in the group (45, 40, 25, and 12), subtract the mean from each and multiply the result by the probability of that outcome occurring. Third, add the four results together. Fourth, find the square root of the result.
← Didn't Know|Knew It →
We have two independent, normally distributed random variables 
and 
such that 
has mean 
and variance 
and 
has mean 
and variance 
. What is the probability distribution of the difference of the random variables, 
?
We have two independent, normally distributed random variables
Tap to reveal answer
The mean for any set of random variables is additive in the sense that
The difference is also additive, so we have
This means the mean of 
is 
.
The variance is additive when the random variables are independent, which they are in this case. But it's additive in the sense that for any real numbers 
(even when negative), we have
.
So for this difference, we have
.
So the mean and variance are 
and 
, respectively. In addition to that, 
is normally distributed because the sum or difference of any set of independent normal random variables is also normally distributed.
The mean for any set of random variables is additive in the sense that
The difference is also additive, so we have
This means the mean of
The variance is additive when the random variables are independent, which they are in this case. But it's additive in the sense that for any real numbers
So for this difference, we have
So the mean and variance are
← Didn't Know|Knew It →
If 
and 
are two independent random variables with 
and 
, what is the standard deviation of the sum, 
If
Tap to reveal answer
If the random variables are independent, the variances are additive in the sense that
.
So then the variance of the sum is
.
The standard deviation is the square root of the variance, so we have
.
If the random variables are independent, the variances are additive in the sense that
So then the variance of the sum is
The standard deviation is the square root of the variance, so we have
← Didn't Know|Knew It →
Consider the discrete random variable 
that takes the following values with the corresponding probabilities:
with 
with 
with 
Compute the probability 
.
Consider the discrete random variable
Compute the probability
Tap to reveal answer
This probability is simple to compute:
We want to add the probability that X is greater or equal to two. This means the probability that X=2 or X=3.
Adding the necessary probabilities we arrive at the solution.
This probability is simple to compute:
We want to add the probability that X is greater or equal to two. This means the probability that X=2 or X=3.
Adding the necessary probabilities we arrive at the solution.
← Didn't Know|Knew It →
Consider the discrete random variable that takes the following values with the corresponding probabilities:
with 
with 
with 
with 
Compute the expected value of the distribution.
Consider the discrete random variable
Compute the expected value of the distribution.
Tap to reveal answer
The expected value is computed as
for any values of x that the random variable takes.
So we have
The expected value is computed as
for any values of x that the random variable takes.
So we have
← Didn't Know|Knew It →
The average number of calories in a Lick Yo' Lips lollipop is 
, with a standard deviation of 
. The calories per lollipop are normally distributed, so what percent of lollipops have more than 
calories?
The average number of calories in a Lick Yo' Lips lollipop is
Tap to reveal answer
The random variable 
number of calories per lollipop, so the answer is
or
The random variable
← Didn't Know|Knew It →
During a week's worth of soccer practice, a player practices 
total free kicks and has a 
chance of scoring. What is the probability that he or she scored at least 
times? Assume each shot is independent.
During a week's worth of soccer practice, a player practices
Tap to reveal answer
Two steps are crucial here.
First, we need to recognize this is a binomial distribution with 
and 
.
Second, we need to realize we can use a normal approximation of the binomial since 
and 
, which are both larger than 5.
With that said, we can calculate a 
-score and its 
-value, keeping in mind that our mean will be 
and our standard deviation will be 
, which is about 
.
Two steps are crucial here.
First, we need to recognize this is a binomial distribution with
Second, we need to realize we can use a normal approximation of the binomial since
With that said, we can calculate a
← Didn't Know|Knew It →