Bivariate Data
Help Questions
AP Statistics › Bivariate Data
On a residual plot, the 

independent variable;
residuals; the independent variable
independent variable; the dependent variable
dependent variable; residuals
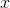

Explanation
A residual plot shows the difference between the actual and expected value, or residual. This goes on the y-axis. The plot shows these residuals in relation to the independent variable.
On a residual plot, the 

independent variable;
residuals; the independent variable
independent variable; the dependent variable
dependent variable; residuals
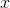

Explanation
A residual plot shows the difference between the actual and expected value, or residual. This goes on the y-axis. The plot shows these residuals in relation to the independent variable.
Which of the following correlation coefficients indicates the strongest relationship between variables?
Explanation
Correlation coefficients range from 1 to -1. The closer to either extreme, the stronger the relationship. The closer to 0, the weaker the relationship.
Which of the following correlation coefficients indicates the strongest relationship between variables?
Explanation
Correlation coefficients range from 1 to -1. The closer to either extreme, the stronger the relationship. The closer to 0, the weaker the relationship.
What transformation should be done to the data set, with its residual shown below, to linearize the data?

take the log of the dependent variable
multiply the dependent variable by a constant k.
Add 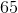
multiply the independent variable by
Nothing, the data set is already linear
Explanation
Taking the log of a data set whose residual is nonrandom is effective in increasing the correleation coefficient and results in a more linear relationship.
What transformation should be done to the data set, with its residual shown below, to linearize the data?

take the log of the dependent variable
multiply the dependent variable by a constant k.
Add 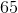
multiply the independent variable by
Nothing, the data set is already linear
Explanation
Taking the log of a data set whose residual is nonrandom is effective in increasing the correleation coefficient and results in a more linear relationship.
It is found that there is a correlation of exactly 
There is enough evidence, with a correlation of 
All of the answer choices are correct
There is a strong association between the two variables.
The association between the two variables is positive
Correlation is measured on a scale of 
Explanation
Under no circumstance will correlation ever equate to causation, regardless of how strong the correlation between two variables is. In this case, all other answer choices are correct.
A national study on cell phone use found the following correlations:
-The correlation between the number of texts sent each day and a person's average credit card debt is 
-The correlation between the number of texts sent each day and the number of books read each month is 
Which of the following statements are true?
i. As the number of texts sent each day increases, average credit card debt increases.
ii. Sending more texts causes people to read less.
iii. A person's average credit card debt is related more strongly to the number of texts sent each day than the number of books read each month is related to the number of texts sent each day.
i and iii
i and ii
ii
ii and iii
iii
Explanation
i is correct because there is a positive correlation between the number of texts sent each day and average credit card debt.
ii is incorrect because the word "cause" was used in the statement. Correlation does not mean causation. There is a relationship between the number of texts sent each day and the number of books that a person reads each month. However, the number of texts sent each day does not cause a person to read a certain number of books each month.
iii is correct because the absolute values of the correlations indicate which correlation is stronger. 

A national study on cell phone use found the following correlations:
-The correlation between the number of texts sent each day and a person's average credit card debt is 
-The correlation between the number of texts sent each day and the number of books read each month is 
Which of the following statements are true?
i. As the number of texts sent each day increases, average credit card debt increases.
ii. Sending more texts causes people to read less.
iii. A person's average credit card debt is related more strongly to the number of texts sent each day than the number of books read each month is related to the number of texts sent each day.
i and iii
i and ii
ii
ii and iii
iii
Explanation
i is correct because there is a positive correlation between the number of texts sent each day and average credit card debt.
ii is incorrect because the word "cause" was used in the statement. Correlation does not mean causation. There is a relationship between the number of texts sent each day and the number of books that a person reads each month. However, the number of texts sent each day does not cause a person to read a certain number of books each month.
iii is correct because the absolute values of the correlations indicate which correlation is stronger. 

It is found that there is a correlation of exactly 
There is enough evidence, with a correlation of 
All of the answer choices are correct
There is a strong association between the two variables.
The association between the two variables is positive
Correlation is measured on a scale of 
Explanation
Under no circumstance will correlation ever equate to causation, regardless of how strong the correlation between two variables is. In this case, all other answer choices are correct.