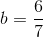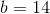Basic Math - Whole Numbers

A city bus has five stops left on its route. At the first stop, people get off. At the second stop, get off. At the third, no one gets off. At the fourth, people get off. At the fifth, there are people left on the bus, and they all get off. How many people were on the bus before the first stop?

Explanation

To solve, create a linear equation:

represents the total number of people on the bus before the first stop.

We then subtract the amount of people that got off at each stop and set that equal to the number of people to get off at the final stop.

Explanation

To solve, create a linear equation:

represents the total number of people on the bus before the first stop.

We then subtract the amount of people that got off at each stop and set that equal to the number of people to get off at the final stop.

Explanation

To solve, create a linear equation:

represents the total number of people on the bus before the first stop.

We then subtract the amount of people that got off at each stop and set that equal to the number of people to get off at the final stop.

Solve for .

$b=\frac{6}{7}$

$b=\frac{7}{6}$

Explanation

Start by isolating the term with to one side. Add 10 on both sides.

Divide both sides by 7.

Solve for .

$b=\frac{6}{7}$

$b=\frac{7}{6}$

Explanation

Start by isolating the term with to one side. Add 10 on both sides.

Divide both sides by 7.

Solve for .

$b=\frac{6}{7}$

$b=\frac{7}{6}$

Explanation

Start by isolating the term with to one side. Add 10 on both sides.

Divide both sides by 7.

What is the solution of the above equation?

Explanation

We can show this using objects:

We can see that only 7 objects are left.

What is the solution of the above equation?

Explanation

We can show this using objects:

We can see that only 7 objects are left.

What is the solution of the above equation?

Explanation

We can show this using objects:

We can see that only 7 objects are left.

If $\small \small 6x+9=45$ , what is $\small x$ equal to?

$\small x=6$

$\small x=9$

$\small x=5$

$\small x=45$

$\small x=1$

Explanation

When solving an equation, we need to find a value of x which makes each side equal each other. We need to remember that $\small 6x+9$ is equal to and the same as $\small 45$ . When we solve an equation, if we make a change on one side, we therefore need to make the exact same change on the other side, so that the equation stays equal and true. To illustrate, let's take a numerical equation:

$\small \small 2\times3+4=10$

If we subtract $\small 4$ from each side, the equation still remains equal:

$\small 2\times3+4-4=10-4$

$\small 2\times3=6$

If we now divide each side by $\small 3$ , the equation still remains equal:

$\small \frac{2\times3}{3}=\frac{6}{3}$

$\small 2=2$

This still holds true even if we have variables in our equation. We can perform the inverse operations to isolate the variable on one side and find out what number it's equal to. To solve our problem then, we need to isolate our $\small x$ term. We can do that by subtracting $\small \small 9$ from each side, the inverse operation of adding $\small \small 9$ :

$\small 6x+9-9=45-9$

$\small 6x=36$

We now want there to be one $\small x$ on the left side. $\small 6x$ is the same thing as $\small 6\times x$ , so we can get rid of the 6 by performing the inverse operation on both sides, i.e. dividing each side by $\small 6$ :