Multi-step Methods - Differential Equations
Card 1 of 4
The two-step Adams-Bashforth method of approximation uses the approximation scheme  .
.
Given that 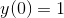 and
and  , use the Adams-Bashforth method to approximate
, use the Adams-Bashforth method to approximate  for
for  with a step size of
with a step size of 
The two-step Adams-Bashforth method of approximation uses the approximation scheme 
Given that 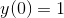



Tap to reveal answer
In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate  by using the explicit Euler method on
by using the explicit Euler method on  .
.
Plugging into 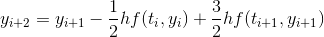 , we have
, we have

 .
.
Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.

In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate 

Plugging into 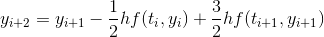

Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.
← Didn't Know|Knew It →
The two-step Adams-Bashforth method of approximation uses the approximation scheme  .
.
Given that 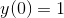 and
and  , use the Adams-Bashforth method to approximate
, use the Adams-Bashforth method to approximate  for
for  with a step size of
with a step size of 
The two-step Adams-Bashforth method of approximation uses the approximation scheme 
Given that 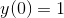



Tap to reveal answer
In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate  by using the explicit Euler method on
by using the explicit Euler method on  .
.
Plugging into 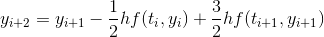 , we have
, we have

 .
.
Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.

In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate 

Plugging into 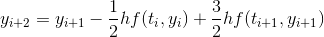

Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.
← Didn't Know|Knew It →
The two-step Adams-Bashforth method of approximation uses the approximation scheme  .
.
Given that 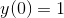 and
and  , use the Adams-Bashforth method to approximate
, use the Adams-Bashforth method to approximate  for
for  with a step size of
with a step size of 
The two-step Adams-Bashforth method of approximation uses the approximation scheme 
Given that 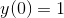



Tap to reveal answer
In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate  by using the explicit Euler method on
by using the explicit Euler method on  .
.
Plugging into 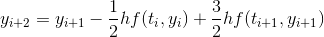 , we have
, we have

 .
.
Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.

In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate 

Plugging into 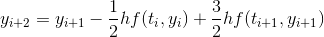

Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.
← Didn't Know|Knew It →
The two-step Adams-Bashforth method of approximation uses the approximation scheme  .
.
Given that 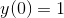 and
and  , use the Adams-Bashforth method to approximate
, use the Adams-Bashforth method to approximate  for
for  with a step size of
with a step size of 
The two-step Adams-Bashforth method of approximation uses the approximation scheme 
Given that 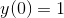



Tap to reveal answer
In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate  by using the explicit Euler method on
by using the explicit Euler method on  .
.
Plugging into 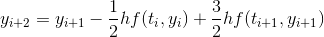 , we have
, we have

 .
.
Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.

In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate 

Plugging into 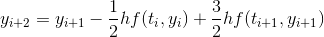

Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.
← Didn't Know|Knew It →