How to find if trapezoids are similar - Geometry
Card 0 of 4
Given Trapezoid  with bases
with bases  and
and  . The trapezoid has midsegment
. The trapezoid has midsegment  , where
, where  and
and  are the midpoints of
are the midpoints of  and
and 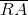 , respectively.
, respectively.
True, false, or undetermined: Trapezoid  Trapezoid
Trapezoid  .
.
Given Trapezoid 






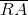
True, false, or undetermined: Trapezoid 

The fact that the trapezoid is isosceles is actually irrelevant. Since  and
and  are the midpoints of legs
are the midpoints of legs  and
and  , it holds by definition that
, it holds by definition that
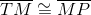
and

It follows that 
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
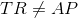
Assume that 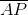 is the longer base - this argument works symmetrically if the opposite is true. Let
is the longer base - this argument works symmetrically if the opposite is true. Let  - equivalently,
- equivalently,  .
.
Since the bases are of unequal length,  . The length of the midsegment
. The length of the midsegment 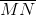 is the arithmetic mean of the lengths of these two bases, so
is the arithmetic mean of the lengths of these two bases, so

Since  , it follows that
, it follows that
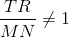 ,
,
and
 .
.
This disproves similarity, since one condition is that corresponding sides must be in proportion.
The fact that the trapezoid is isosceles is actually irrelevant. Since 



and
It follows that
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
Assume that 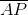


Since the bases are of unequal length, 
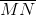
Since 
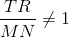
and

This disproves similarity, since one condition is that corresponding sides must be in proportion.
Compare your answer with the correct one above
Given Trapezoid  with bases
with bases  and
and  . The trapezoid has midsegment
. The trapezoid has midsegment  , where
, where  and
and  are the midpoints of
are the midpoints of  and
and 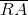 , respectively.
, respectively.
True, false, or undetermined: Trapezoid  Trapezoid
Trapezoid  .
.
Given Trapezoid 






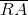
True, false, or undetermined: Trapezoid 

The fact that the trapezoid is isosceles is actually irrelevant. Since  and
and  are the midpoints of legs
are the midpoints of legs  and
and  , it holds by definition that
, it holds by definition that
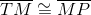
and

It follows that 
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
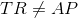
Assume that 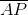 is the longer base - this argument works symmetrically if the opposite is true. Let
is the longer base - this argument works symmetrically if the opposite is true. Let  - equivalently,
- equivalently,  .
.
Since the bases are of unequal length,  . The length of the midsegment
. The length of the midsegment 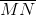 is the arithmetic mean of the lengths of these two bases, so
is the arithmetic mean of the lengths of these two bases, so

Since  , it follows that
, it follows that
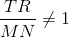 ,
,
and
 .
.
This disproves similarity, since one condition is that corresponding sides must be in proportion.
The fact that the trapezoid is isosceles is actually irrelevant. Since 



and
It follows that
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
Assume that 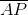


Since the bases are of unequal length, 
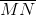
Since 
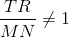
and

This disproves similarity, since one condition is that corresponding sides must be in proportion.
Compare your answer with the correct one above
Given Trapezoid  with bases
with bases  and
and  . The trapezoid has midsegment
. The trapezoid has midsegment  , where
, where  and
and  are the midpoints of
are the midpoints of  and
and 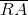 , respectively.
, respectively.
True, false, or undetermined: Trapezoid  Trapezoid
Trapezoid  .
.
Given Trapezoid 






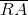
True, false, or undetermined: Trapezoid 

The fact that the trapezoid is isosceles is actually irrelevant. Since  and
and  are the midpoints of legs
are the midpoints of legs  and
and  , it holds by definition that
, it holds by definition that
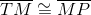
and

It follows that 
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
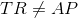
Assume that 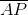 is the longer base - this argument works symmetrically if the opposite is true. Let
is the longer base - this argument works symmetrically if the opposite is true. Let  - equivalently,
- equivalently,  .
.
Since the bases are of unequal length,  . The length of the midsegment
. The length of the midsegment 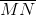 is the arithmetic mean of the lengths of these two bases, so
is the arithmetic mean of the lengths of these two bases, so

Since  , it follows that
, it follows that
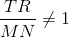 ,
,
and
 .
.
This disproves similarity, since one condition is that corresponding sides must be in proportion.
The fact that the trapezoid is isosceles is actually irrelevant. Since 



and
It follows that
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
Assume that 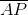


Since the bases are of unequal length, 
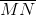
Since 
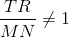
and

This disproves similarity, since one condition is that corresponding sides must be in proportion.
Compare your answer with the correct one above
Given Trapezoid  with bases
with bases  and
and  . The trapezoid has midsegment
. The trapezoid has midsegment  , where
, where  and
and  are the midpoints of
are the midpoints of  and
and 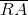 , respectively.
, respectively.
True, false, or undetermined: Trapezoid  Trapezoid
Trapezoid  .
.
Given Trapezoid 






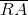
True, false, or undetermined: Trapezoid 

The fact that the trapezoid is isosceles is actually irrelevant. Since  and
and  are the midpoints of legs
are the midpoints of legs  and
and  , it holds by definition that
, it holds by definition that
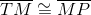
and

It follows that 
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
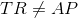
Assume that 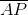 is the longer base - this argument works symmetrically if the opposite is true. Let
is the longer base - this argument works symmetrically if the opposite is true. Let  - equivalently,
- equivalently,  .
.
Since the bases are of unequal length,  . The length of the midsegment
. The length of the midsegment 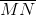 is the arithmetic mean of the lengths of these two bases, so
is the arithmetic mean of the lengths of these two bases, so

Since  , it follows that
, it follows that
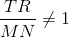 ,
,
and
 .
.
This disproves similarity, since one condition is that corresponding sides must be in proportion.
The fact that the trapezoid is isosceles is actually irrelevant. Since 



and
It follows that
However, the bases of each trapezoid are noncongruent, by definition, so, in particular,
Assume that 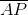


Since the bases are of unequal length, 
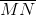
Since 
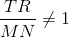
and

This disproves similarity, since one condition is that corresponding sides must be in proportion.
Compare your answer with the correct one above