Right Triangles - Geometry
Card 0 of 1412
Figures  and
and  are triangles.
are triangles.


Are  and
and  congruent?
congruent?
Figures 


Are 

We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of  . A triangle whose sides are in this ratio is a
. A triangle whose sides are in this ratio is a  , where the shorter sides lies opposite the
, where the shorter sides lies opposite the  angles, and the longer side is the hypotenuse and lies opposite the right angle. So we know the corresponding angles are equal. Therefore, the triangles are congruent.
angles, and the longer side is the hypotenuse and lies opposite the right angle. So we know the corresponding angles are equal. Therefore, the triangles are congruent.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 


Compare your answer with the correct one above
Figures  and
and  are triangles.
are triangles.


Are  and
and  congruent?
congruent?
Figures 


Are 

We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of  .
.
Simplify the ratio by dividing by 



Thus, the corresponding sides are in the ratio  and we know both triangles are
and we know both triangles are  triangles. Since the corresponding angles and the corresponding sides are equal, the triangles are congruent.
triangles. Since the corresponding angles and the corresponding sides are equal, the triangles are congruent.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 
Simplify the ratio by dividing by
Thus, the corresponding sides are in the ratio 

Compare your answer with the correct one above
Are these right triangles congruent?

Are these right triangles congruent?
Right now we can't directly compare these triangles because we do not know all three side lengths. However, we can use Pythagorean Theorem to determine both missing sides. The left triangle is missing the hypotenuse:




The right triangle is missing one of the legs:

 subtract 2,304 from both sides
subtract 2,304 from both sides


This means that the two triangles both have side lengths 48, 55, 73, so they must be congruent.
Right now we can't directly compare these triangles because we do not know all three side lengths. However, we can use Pythagorean Theorem to determine both missing sides. The left triangle is missing the hypotenuse:
The right triangle is missing one of the legs:

This means that the two triangles both have side lengths 48, 55, 73, so they must be congruent.
Compare your answer with the correct one above
The hypotenuse and acute angle are given for several triangles. Which if any are congruent? Triangle A- Hypotenuse=15; acute angle=56 degrees. Triangle B- Hypotenuse=18; acute angle=56 degrees. Triangle C-Hypotenuse=18; acute angle= 45 degrees.
The hypotenuse and acute angle are given for several triangles. Which if any are congruent? Triangle A- Hypotenuse=15; acute angle=56 degrees. Triangle B- Hypotenuse=18; acute angle=56 degrees. Triangle C-Hypotenuse=18; acute angle= 45 degrees.
The correct answer is none of these. There are several pairs of angles and sides or sides and angles that must be the same in order for two triangles to be congruent.
In our case, we need the acute angle and the hypotenuse to both be equal. No two triangles above have this relationship and therefore no two are congruent.
The correct answer is none of these. There are several pairs of angles and sides or sides and angles that must be the same in order for two triangles to be congruent.
In our case, we need the acute angle and the hypotenuse to both be equal. No two triangles above have this relationship and therefore no two are congruent.
Compare your answer with the correct one above
Given:  and
and  .
.
 and
and  are both right angles.
are both right angles.


True or false: From the above information, it follows that  .
.
Given: 



True or false: From the above information, it follows that 
If we seek to prove that  , then
, then  ,
,  , and
, and  correspond to
correspond to  ,
,  , and
, and  , respectively.
, respectively.
By the Hypotenuse-Leg Theorem (HL), if the hypotenuse and one leg of a triangle are congruent to those of another, the triangles are congruent.
 and
and  are both right angles, so
are both right angles, so  and
and  are both right triangles.
are both right triangles.  and
and  are congruent corresponding sides, and moreover, since, each includes the right-angle vertex as an endpoint, they are congruent corresponding legs.
are congruent corresponding sides, and moreover, since, each includes the right-angle vertex as an endpoint, they are congruent corresponding legs.  and
and  are opposite the right angles, making them congruent corresponding hypotenuses.
are opposite the right angles, making them congruent corresponding hypotenuses.
The conditions of HL are satisfied, so  .
.
If we seek to prove that 






By the Hypotenuse-Leg Theorem (HL), if the hypotenuse and one leg of a triangle are congruent to those of another, the triangles are congruent.








The conditions of HL are satisfied, so 
Compare your answer with the correct one above
Given:  and
and  .
.
 and
and  are both right angles.
are both right angles.


True or false: From the given information, it follows that  .
.
Given: 



True or false: From the given information, it follows that 
The congruence of  and
and  cannot be proved from the given information alone. Examine the two triangles below:
cannot be proved from the given information alone. Examine the two triangles below:

 ,
,  , and
, and  and
and  are both right angles, so the conditions of the problem are met; however, since the sides are not congruent between triangles - for example,
are both right angles, so the conditions of the problem are met; however, since the sides are not congruent between triangles - for example,  - the triangles are not congruent either.
- the triangles are not congruent either.
The congruence of 







Compare your answer with the correct one above
 ;
;  is a right angle;
is a right angle;  ;
;  ;
; 
Find  .
.




Find 
Since  and
and  is a right angle,
is a right angle,  is also a right angle.
is also a right angle.
 is the hypotenuse of the first triangle; since one of its legs
is the hypotenuse of the first triangle; since one of its legs  is half the length of that hypotenuse,
is half the length of that hypotenuse,  is 30-60-90 with
is 30-60-90 with  the shorter leg and
the shorter leg and  the longer.
the longer.
Because the two are similar triangles,  is the hypotenuse of the second triangle, and
is the hypotenuse of the second triangle, and  is its longer leg.
is its longer leg.
Therefore,  .
.
Since 







Because the two are similar triangles, 

Therefore, 
Compare your answer with the correct one above
Which of the following is sufficient to say that two right triangles are similar?
Which of the following is sufficient to say that two right triangles are similar?
If all three angles of a triangle are congruent but the sides are not, then one of the triangles is a scaled up version of the other. When this happens the proportions between the sides still remains unchanged which is the criteria for similarity.
If all three angles of a triangle are congruent but the sides are not, then one of the triangles is a scaled up version of the other. When this happens the proportions between the sides still remains unchanged which is the criteria for similarity.
Compare your answer with the correct one above
Which of the following statements is true regarding the two triangles?
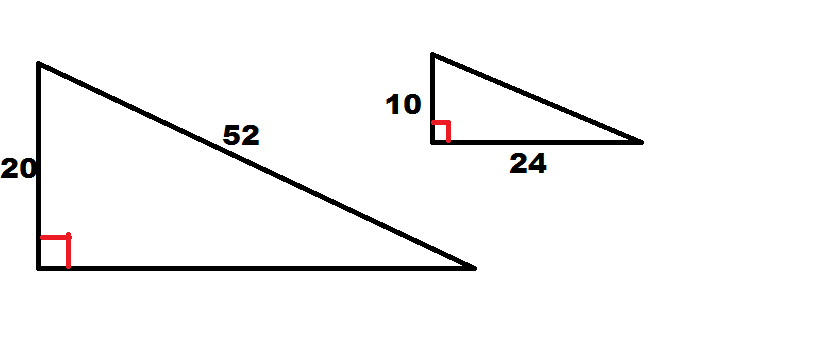
Which of the following statements is true regarding the two triangles?

Though we must do a little work, we can show these triangles are similar. First, right triangles are not necessarily always similar. They must meet the necessary criteria like any other triangles; furthermore, there is no Hypotenuse-Leg Theorem for similarity, only for congruence; therefore, we can eliminate two answer choices.
However, we can use the Pythagorean Theorem with the smaller triangle to find the missing leg. Doing so gives us a length of 48. Comparing the ratio of the shorter legs in each trangle to the ratio of the longer legs we get


In both cases, the leg of the larger triangle is twice as long as the corresponding leg in the smaller triangle. Given that the angle between the two legs is a right angle in each triangle, these angles are congruent. We now have enough evidence to conclude similarity by Side-Angle-Side.
Though we must do a little work, we can show these triangles are similar. First, right triangles are not necessarily always similar. They must meet the necessary criteria like any other triangles; furthermore, there is no Hypotenuse-Leg Theorem for similarity, only for congruence; therefore, we can eliminate two answer choices.
However, we can use the Pythagorean Theorem with the smaller triangle to find the missing leg. Doing so gives us a length of 48. Comparing the ratio of the shorter legs in each trangle to the ratio of the longer legs we get
In both cases, the leg of the larger triangle is twice as long as the corresponding leg in the smaller triangle. Given that the angle between the two legs is a right angle in each triangle, these angles are congruent. We now have enough evidence to conclude similarity by Side-Angle-Side.
Compare your answer with the correct one above
Two triangles,  and
and  , are similar when:
, are similar when:
Two triangles, 

The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. Either condition alone is not sufficient. If two figures have both equal corresponding angles and equal corresponding lengths then they are congruent, not similar.
The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. Either condition alone is not sufficient. If two figures have both equal corresponding angles and equal corresponding lengths then they are congruent, not similar.
Compare your answer with the correct one above
 and
and  are triangles.
are triangles.



Are  and
and  similar?
similar?



Are 

The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. In other words, we need to know both the measures of the corresponding angles and the lengths of the corresponding sides. In this case, we know only the measures of  and
and  . We don't know the measures of any of the other angles or the lengths of any of the sides, so we cannot answer the question -- they might be similar, or they might not be.
. We don't know the measures of any of the other angles or the lengths of any of the sides, so we cannot answer the question -- they might be similar, or they might not be.
It's not enough to know that both figures are right triangles, nor can we assume that angles are the same measurement because they appear to be.
Similar triangles do not have to be the same size.
The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. In other words, we need to know both the measures of the corresponding angles and the lengths of the corresponding sides. In this case, we know only the measures of 

It's not enough to know that both figures are right triangles, nor can we assume that angles are the same measurement because they appear to be.
Similar triangles do not have to be the same size.
Compare your answer with the correct one above
 and
and  are similar triangles.
are similar triangles.





What is the length of  ?
?



What is the length of 
Since  and
and  are similar triangles, we know that they have proportional corresponding lengths. We must determine which sides correspond. Here, we know
are similar triangles, we know that they have proportional corresponding lengths. We must determine which sides correspond. Here, we know  corresponds to
corresponds to  because both line segments lie opposite
because both line segments lie opposite  angles and between
angles and between  and
and  angles. Likewise, we know
angles. Likewise, we know  corresponds to
corresponds to  because both line segments lie opposite
because both line segments lie opposite  angles and between
angles and between  and
and  angles. We can use this information to set up a proportion and solve for the length of
angles. We can use this information to set up a proportion and solve for the length of  .
.

Substitute the known values.

Cross-multiply and simplify.

 and
and  result from setting up an incorrect proportion.
result from setting up an incorrect proportion.  results from incorrectly multiplying
results from incorrectly multiplying  and
and  .
.
Since 












Substitute the known values.
Cross-multiply and simplify.





Compare your answer with the correct one above
Are these triangles similar? If so, list the scale factor.

Are these triangles similar? If so, list the scale factor.
The two triangles are similar, but we can't be sure of that until we can compare all three corresponding pairs of sides and make sure the ratios are the same. In order to do that, we first have to solve for the missing sides using the Pythagorean Theorem.




The smaller triangle is missing not the hypotenuse, c, but one of the legs, so we'll use the formula slightly differently.

 subtract 36 from both sides
subtract 36 from both sides


Now we can compare all three ratios of corresponding sides:
 one way of comparing these ratios is to simplify them.
one way of comparing these ratios is to simplify them.
We can simplify the leftmost ratio by dividing top and bottom by 3 and getting  .
.
We can simplify the middle ratio by dividing top and bottom by 4 and getting  .
.
Finally, we can simplify the ratio on the right by dividing top and bottom by 5 and getting  .
.
This means that the triangles are definitely similar, and  is the scale factor.
is the scale factor.
The two triangles are similar, but we can't be sure of that until we can compare all three corresponding pairs of sides and make sure the ratios are the same. In order to do that, we first have to solve for the missing sides using the Pythagorean Theorem.
The smaller triangle is missing not the hypotenuse, c, but one of the legs, so we'll use the formula slightly differently.

Now we can compare all three ratios of corresponding sides:

We can simplify the leftmost ratio by dividing top and bottom by 3 and getting 
We can simplify the middle ratio by dividing top and bottom by 4 and getting 
Finally, we can simplify the ratio on the right by dividing top and bottom by 5 and getting 
This means that the triangles are definitely similar, and 
Compare your answer with the correct one above
Are these right triangles similar? If so, state the scale factor.

Are these right triangles similar? If so, state the scale factor.
In order to compare these triangles and determine if they are similar, we need to know all three side lengths in both triangles. To get the missing ones, we can use Pythagorean Theorem:


 take the square root
take the square root

The other triangle is missing one of the legs rather than the hypotenuse, so we'll adjust accordingly:

 subtract 36 from both sides
subtract 36 from both sides


Now we can compare ratios of corresponding sides:

The first ratio simplifies to  , but we can't simplify the others any more than they already are. The three ratios clearly do not match, so these are not similar triangles.
, but we can't simplify the others any more than they already are. The three ratios clearly do not match, so these are not similar triangles.
In order to compare these triangles and determine if they are similar, we need to know all three side lengths in both triangles. To get the missing ones, we can use Pythagorean Theorem:

The other triangle is missing one of the legs rather than the hypotenuse, so we'll adjust accordingly:

Now we can compare ratios of corresponding sides:
The first ratio simplifies to 
Compare your answer with the correct one above
Given:  and
and  .
.
 and
and  are both right angles.
are both right angles.


True or false: From the given information, it follows that  .
.
Given: 



True or false: From the given information, it follows that 
If we seek to prove that  , then
, then  ,
,  , and
, and  correspond to
correspond to  ,
,  , and
, and  , respectively.
, respectively.
By the Side-Angle-Side Similarity Theorem (SASS), if two sides of a triangle are in proportion with the corresponding sides of another triangle, and the included angles are congruent, then the triangles are similar.
 and
and  , so by the Division Property of Equality,
, so by the Division Property of Equality,  . Also,
. Also,  and
and  , their respective included angles, are both right angles, so
, their respective included angles, are both right angles, so  . The conditions of SASS are met, so
. The conditions of SASS are met, so 
If we seek to prove that 






By the Side-Angle-Side Similarity Theorem (SASS), if two sides of a triangle are in proportion with the corresponding sides of another triangle, and the included angles are congruent, then the triangles are similar.






Compare your answer with the correct one above
The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?
The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?
We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.
We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.
Compare your answer with the correct one above
A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?
A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?
The area of a triangle is denoted by the equation 1/2 b x h.
b stands for the length of the base, and h stands for the height.
Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.
So, 12-5 = 7 for the total perimeter of the base and height.
7 does not divide cleanly by two, but it does break down into 3 and 4,
and 1/2 (3x4) yields 6.
Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here
The area of a triangle is denoted by the equation 1/2 b x h.
b stands for the length of the base, and h stands for the height.
Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.
So, 12-5 = 7 for the total perimeter of the base and height.
7 does not divide cleanly by two, but it does break down into 3 and 4,
and 1/2 (3x4) yields 6.
Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here
Compare your answer with the correct one above
The length of one leg of an equilateral triangle is 6. What is the area of the triangle?
The length of one leg of an equilateral triangle is 6. What is the area of the triangle?

The base is equal to 6.
The height of an quilateral triangle is equal to  , where
, where  is the length of the base.
is the length of the base.

The base is equal to 6.
The height of an quilateral triangle is equal to 

Compare your answer with the correct one above

Given:
A = 3 cm
B = 4 cm
What is the area of the right triangle ABC?

Given:
A = 3 cm
B = 4 cm
What is the area of the right triangle ABC?
The area of a triangle is given by the equation:

Since the base leg of the given triangle is 4 cm, while the height is 3 cm, this gives:

The area of a triangle is given by the equation:
Since the base leg of the given triangle is 4 cm, while the height is 3 cm, this gives:
Compare your answer with the correct one above

Given:
A = 4 cm
B = 6 cm
What is the area of the right triangle ABC?

Given:
A = 4 cm
B = 6 cm
What is the area of the right triangle ABC?
The area of a triangle is given by the equation:

Since the base leg of the given triangle is 4 cm, while the height is 3 cm, this gives:

The area of a triangle is given by the equation:
Since the base leg of the given triangle is 4 cm, while the height is 3 cm, this gives:
Compare your answer with the correct one above