Functions and Graphs - GRE Quantitative Reasoning

Card 0 of 436

Question

What kind of function is this: $f(x)=\sqrt[3] {x-1}$ ?

Answer

Step 1: Look at the equation.. $\sqrt[3] {x-1}$ . The cube-root outside of the function determines what the answer is..

The function is a cube-root function.

Note:

Square function,
Cube function,
Rational function, $\frac {1}{x}$ (if )

Compare your answer with the correct one above

Question

What kind of function is

Answer

Step 1: To classify any function, find the degree of that function. The degree of a function is the highest exponent.

Step 2: Find degree of .

The degree is 3..

Step 3: Find what kind of function has degree of 3:

A cubic function has a degree of 3...

A square function has a degree of 2
A line has a degree of 1

Compare your answer with the correct one above

Question

What kind of function is $\large y=x^2$

Answer

Step 1: Define some basic graphs and their functions...

Line functions have an equation $\large ax+b$ , where $\large \large {a,b}\in \mathbb{R}$
Parabola (Quadratic functions) have an equation $\large ax^2+bx+c$ or $\large ax^2+c$ or $\large ax^2$ , where $\large \large {a,b,c}\in \mathbb{R}$

Cubic functions have an equation $\large \large ax^3 \pm b$ , where $\large {a,b} \in \mathbb{R}$

Step 2: Determine what type of function is given...

The equation given is a parabola...

Compare your answer with the correct one above

Question

What kind of function is $\large y=\sqrt[3] {x+6}-4$ ?

Answer

Quadratic functions have at least an $\large x^2$ term.
Absolute Functions have $\large \left | x\right |$ .

Cube-Root functions have $\large \sqrt[3]{x}$

The function $\large y$ is a cube-root function because it shares $\large \sqrt[3]{x}$

Compare your answer with the correct one above

Question

What is the domain of $\frac{x+1}{\sqrt{4-x^2}}$ ?

Answer

Step 1: We need to determine what kind of function we have here. We have a rational function.

Step 2: Since we have a rational function, the denominator cannot be equal to . We will equal the denominator to and find the values of that make the bottom zero.

$\sqrt{4-x^2}=0$
Square both sides:
$(\sqrt {4-x^2})^2=0^2\rightarrow 4-x^2=0$
Add to both sides of the equal sign:

Simplify:

Take the square root of both sides
$\sqrt{4}=\sqrt {x^2}\rightarrow \pm2=x$

However, we said earlier that these two solutions cannot be values of x, so we must change the sign:

$\pm 2 eq x$

Step 3: We need to write the solution in interval notation form.

The smallest number we can plug in for is $-\infty$ , and the biggest is $+\infty$ . cannot be and , but it can be anything else. So, we should have three intervals:

Between $-\infty$ and , which is written as $(-\infty,-2)$

Between and , which is written as

Between and $+\infty$ , which is written as $(2,+\infty)$

The full solution in interval notation is $(-\infty,-2)\cup (-2,2)\cup (2,+\infty)$ .

Compare your answer with the correct one above

Question

What is the domain of: $\sqrt{x+3}$

Answer

Step 1: We have a square root here, where the inside of the radical must be greater or equal than , so we get a real answer.

Step 2: Set the inside equation greater or equal than zero...

$x+3 \ge 0$

Step 3: Solve for x...

$x \ge -3$ ... Write this in interval notation. is the leftmost boundary, infinity is the right boundary. has a bracket with it, infinity does not..

Final Answer: $[-3,+\infty)$

Compare your answer with the correct one above

Question

What is the range of the function?
$f(x) = \begin{cases} x^2, & x>2\ -x+1, & x\leq 2 \end{cases} \bigg}$

Answer

Step 1: Find the minimum and maximum range for each equation..

Let's start with ..

I will plug in , I get . This is in my domain, which means it's the lowest value for the range. The maximum value is $+\infty$

$-x+1, x\leq 2$

Minimum range: $-\infty$

Maximum range:

Step 2: Write the solution in interval notation form:

$-\infty, +\infty$ always get parentheses

get brackets because they are in my range...

Answer:

$(-\infty, -1] \cup [9,+\infty)$

Compare your answer with the correct one above

Question

What is the domain of the function $y=-\sqrt{-3x+6}$ ?

Answer

For a function defined by an expression with variable the domain of is the set of all real numbers that the variable can take such that the expression defining the function is real.

The expression defining function contains a square root.

$y=-\sqrt{-3x+6}$ .

The domain is the set of all first elements of ordered pairs or

Because there cannot be a negative inside the radical sign, set the inside of the radical $\geq 0$ and solve. The expression under the radical has to satisfy the condition $-3x+6\geq 0$ for the function to take real values.

Solve:

$-3x+6\geq 0$

Subtract from both sides of the equation.

$-3x - 6 + 6 \geq 0 + -6$

$-3x \geq -6$

Divide both sides of the equation by .

$\frac{-3x}{-3} \geq \frac{-6}{-3}$

Because you are dividing both sides of the equation by a negative integer this will change the sign from $\geq$ to $\leq$ .

$x \leq 2$

The domain or d is all $x \leq 2.$

Compare your answer with the correct one above

Question

What is the domain and the range for this set of numbers?

$\left { (-4,3) (-3,3)(-2,3)(-1,3)\right }$

Answer

The domain is the set of all first elements of ordered pairs (x-coordinates). The range is the set of all second elements of ordered pairs (y-coordinates).

Given this set of ordered pairs $\left { (-4,3) (-3,3)(-2,3)(-1,3)\right }$ , the

domain is $\left { -4,-3,-2,-1\right }$ and the range is $\left { 3\right }$ .

Note: If a value of a coordinate is repeated, it only gets listed once in the set.

Compare your answer with the correct one above

Question

What is the range of the function $f(x) = x^{2} -3$ , when the domain is $\left { -3,-2,-1,0,1,2,3\right }$ ?

Answer

The domain is the set of all first elements of ordered pairs (x-coordinates). The range is the set of all second elements of ordered pairs (y-coordinates).

$f(x) = x^{2} -3$ domain or values of $\left { -3,-2,-1,0,1,2,3\right }$

Plug all of the values of that have been given into the equation

$y=x^{2} -3$

$y=-3^{2} -3 = 9-3 =6$

$y = -2^{2} -3 = 4-3=1$

$y =-1^{2} -3 = 1-3 = -2$

$y = 0^{2} -3 = 0-3 = -3$

$y = 1^{2} - 3 = 1-3=-2$

$y= 2^{2} -3 = 4-3=1$

$y = 3^{2} - 3 = 9-3=6$

Even though some of the values of are repeated, they are only listed once in the set..

The range, or all values of for the function are

$\left {-3,-2,1,6\right }$ .

Compare your answer with the correct one above

Question

What is the range of the function $g(x) =x^{2} +8$ if the domain is $\left {2,3,4\right }$ ?

Answer

The domain is the set of all first elements of ordered pairs (x-coordinates). The range is the set of all second elements of ordered pairs (y-coordinates).

The domain, or all values of $\left { 2,3,4\right }$ .

In order to get the range or all values of insert the given values of (the domain) into the equation and solve for (the range).

$y = 2^{2} +8 = 4+8 = 12$

$y =3^{2} +8 = 9+8 = 17$

$y = 4^{2} + 8 = 16+ 8 =24$

The range for the function with the domain of $\left { 2,3,4\right }$ is

$\left { 12,17,24\right }$ .

Compare your answer with the correct one above

Question

What is the domain and range for this graph?

Answer

The ordered pairs represented on the graph are: $\left { (0,2), (1,3), (2,4), (-1,1), (-2,0)\right }$

The domain is the set of all first elements of ordered pairs (x-coordinates). The range is the set of all second elements of ordered pairs (y-coordinates).

The domain is $\left {-2,-1, 0, 1, 2\right }$ ; the range is $\left {0,1,2,3,4\right }$ .

Compare your answer with the correct one above

Question

Find the domain for the function $f(x) = \sqrt{2x-10}$ ?

Answer

For a function defined by an expression with variable the domain of is the set of all real numbers that the variable can take such that the expression defining the function is real.

The expression defining function $f(x) = \sqrt{2x-10}$ contains a square root. The expression under the radical has to satisfy the condition $2x-10\geq 0$ for the function to take real values.

Solve $2x-10\geq 0$

Add to both sides of the equation.

$2x-10 +10\geq 0+10$

$2x\geq 10$

Divide both sides by .

$2x\div2 \geq10\div2$

The domain is all $x\geq5.$

Compare your answer with the correct one above

Question

Find the domain and the range of the inverse of a relation with this set of coordinates:

$\left { (0,1) (2,3) (-2,-3) (4,1) \right }$

Answer

To find the domain and the range of the inverse of a relation with this set of coordinates, first find the domain and range of the set of coordinates given.

The domain is all of the -coordinates and the range is all of the -coordinates. Remember, if a coordinate is the same, it is only listed once.

The domain of $\left { (0,1) (2,3) (-2,-3) (4,1) \right }$ is

$\left { -2,0,2,4\right }$ and the range is $\left { -3,1,3 \right }$ .

However, the question is asking for the domain and the range of the inverse. So, the values of (the domain) will now become the values of , (the range) and the values of (the range) will become the values of , or the domain.

The domain for the inverse is $\left { -3,1,3\right }$ and the range is $\left {-2, 0,2,4\right }$ .

Compare your answer with the correct one above

Question

The surface area of a cube is the total outside area of that cube. A cube has a side length of at least The surface area is a function of side length. What is the domain (side length) and the range (surface area)?

Answer

The surface area of a cube is the total outside area of that cube. The formula to find the Area of a cube is $A=6s^{2}$ .

A cube has a side length of at least inches. The surface area is a function of side length. What is the domain (side length) and the range (surface area)?

The independent variable is the length of the side. The domain consists of numbers that represent the length of sides. The problem states that the length of the sides is at least inches. So, the domain is all numbers greater than or equal to four.

$D\left { s\mid s\geq 4\right }$

The range consists of the numbers that corresponds with the chosen values in a function.

To find the range, find the Area of the cube with the length of the side measuring inches; this is the smallest value that (or the side length measurement), can be equal to.

$A \geq 6 (4^{2})$

$A\geq6 (16)$

$A\geq 96$

$R\left { A\mid A\geq 96\right }$

The correct answer is $D\left { s\mid s\geq 4\right }$ ; $R\left { A\mid A\geq 96\right }$

Compare your answer with the correct one above

Question

At what point does the line cross the y-axis?

Answer

Step 1: Rearrange the terms into the form y=mx+b. Move the to the other side.

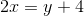
Step 2: Move the 4 to the other side.

Step 3: When the line crosses the y-axis, the x value is zero. We will plug in for x and find the y value.

$\rightarrow y=-4$

So, the point where this line crosses the y-axis is

Compare your answer with the correct one above

Question

Find the minimum distance between the point and the following line:

$f(x)=-\frac{1}{3}x+2$

Answer

The minimum distance from the point to the line would be found by drawing a segment perpendicular to the line directly to the point. Our first step is to find the equation of the new line that connects the point to the line given in the problem. Because we know this new line is perpendicular to the line we're finding the distance to, we know its slope will be the negative inverse of the line its perpendicular to. So if the line we're finding the distance to is:

$f(x)=-\frac{1}{3}x+2$

Then its slope is -1/3, so the slope of a line perpendicular to it would be 3. Now that we know the slope of the line that will give the shortest distance from the point to the given line, we can plug the coordinates of our point into the formula for a line to get the full equation of the new line:

$-4=3(-2)+b\rightarrow b=2$

Now that we know the equation of our perpendicular line, our next step is to find the point where it intersects the line given in the problem:

$3x+2=-\frac{1}{3}x+2$

$\frac{10}{3}x=0\rightarrow x=0$

So if the lines intersect at x=0, we plug that value into either equation to find the y coordinate of the point where the lines intersect, which is the point on the line closest to the point given in the problem and therefore tells us the location of the minimum distance from the point to the line:

So we now know we want to find the distance between the following two points:

and

Using the following formula for the distance between two points, which we can see is just an application of the Pythagorean Theorem, we can plug in the values of our two points and calculate the shortest distance between the point and line given in the problem:

$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

$d=\sqrt{(0-(-2))^2+(2-(-4))^2}=\sqrt{(2)^2+(6)^2}=\sqrt{40}$

Which we can then simplify by factoring the radical:

$\sqrt{40}=\sqrt{4\cdot 10}=2\sqrt{10}$

Compare your answer with the correct one above

Question

What is the shortest distance between the line and the origin?

Answer

The shortest distance from a point to a line is always going to be along a path perpendicular to that line. To be perpendicular to our line, we need a slope of $-\frac{1}{3}$ .

To find the equation of our line, we can simply use point-slope form, using the origin, giving us

$y-0=\left(-\frac{1}{3}\right)(x-0)$ which simplifies to $y=-\frac{x}{3}$ .

Now we want to know where this line intersects with our given line. We simply set them equal to each other, giving us $-\frac{x}{3}=3x-4$ .

If we multiply each side by , we get .

We can then add to each side, giving us .

Finally we divide by , giving us $x=\frac{6}{5}$ .

This is the x-coordinate of their intersection. To find the y-coordinate, we plug $\frac{6}{5}$ into $y=-\frac{x}{3}$ , giving us $y=-\frac{2}{5}$ .

Therefore, our point of intersection must be $\left(\frac{6}{5},-\frac{2}{5}\right)$ .

We then use the distance formula $d=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}$ using $\left(\frac{6}{5},-\frac{2}{5}\right)$ and the origin.

This give us $d=\sqrt{\left(\frac{36}{25}\right)+\left(\frac{4}{25}\right)}=\sqrt{\frac{40}{25}}=\frac{2\sqrt{10}}{5}$ .

Compare your answer with the correct one above

Question

Find the distance from point $\left ( 1,-\frac{1}{2}\right )$ to the line .

Answer

Draw a line that connects the point and intersects the line at a perpendicular angle.

The vertical distance from the point $\left ( 1,-\frac{1}{2}\right )$ to the line will be the difference of the 2 y-values.

The distance can never be negative.

$5-\left(-\frac{1}{2}\right) = \frac{10}{2}+\frac{1}{2}=\frac{11}{2}$

Compare your answer with the correct one above

Question

Find the distance between point $(\frac{1}{2},\frac{1}{2})$ to the line $x=-\frac{1}{2}$ .

Answer

Distance cannot be a negative number. The function $x=-\frac{1}{2}$ is a vertical line. Subtract the value of the line to the x-value of the given point to find the distance.

$D=\left | (-\frac{1}{2})-\frac{1}{2} \right | = \left | -1\right |=1$

Compare your answer with the correct one above

Tap the card to reveal the answer