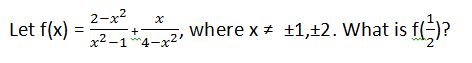How to evaluate rational expressions - GRE Quantitative Reasoning
Card 1 of 112
If √(ab) = 8, and _a_2 = b, what is a?
If √(ab) = 8, and _a_2 = b, what is a?
Tap to reveal answer
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Find the product of 
and 
.
Find the product of
Tap to reveal answer
Solve the first equation for 
.
Solve the second equation for 
.
The final step is to multiply 
and 
.
Solve the first equation for
Solve the second equation for
The final step is to multiply
← Didn't Know|Knew It →
Evaluate the following rational expression, if 
:
Evaluate the following rational expression, if
Tap to reveal answer
To evaluate, simply plug in the number 
for 
:
Remembering to use order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution.
To evaluate, simply plug in the number
Remembering to use order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution.
← Didn't Know|Knew It →
If 
, find 
.
If
Tap to reveal answer
To solve, simply plug in 
for 
:
Remembering to use the correct order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final answer.
First do the multiplication that is in the numerator.
Now do the subtraction in the denominator.
To solve, simply plug in
Remembering to use the correct order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final answer.
First do the multiplication that is in the numerator.
Now do the subtraction in the denominator.
← Didn't Know|Knew It →
Find 
if 
.
Find
Tap to reveal answer
To solve, simply plug in 
for 
:
Remembering to use the correct order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at the final solution.
Also recall that when a negative number is squared it becomes a positive number. This is also true when we multiply two negative numbers together.
To solve, simply plug in
Remembering to use the correct order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at the final solution.
Also recall that when a negative number is squared it becomes a positive number. This is also true when we multiply two negative numbers together.
← Didn't Know|Knew It →
Evaluate 
if 
.
Evaluate
Tap to reveal answer
To evaluate, merely plug in 
for 
:
Remembering order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution.
From here we can further reduce the fraction by factoring out a two from both the numerator and denominator.
Canceling out the two's we get:
To evaluate, merely plug in
Remembering order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution.
From here we can further reduce the fraction by factoring out a two from both the numerator and denominator.
Canceling out the two's we get:
← Didn't Know|Knew It →
Evaluate 
if 
.
Evaluate
Tap to reveal answer
To solve, simply plug in 
for 
:
Recall that when a negative number is divided by another negative number it results in a positive number.
To solve, simply plug in
Recall that when a negative number is divided by another negative number it results in a positive number.
← Didn't Know|Knew It →
Evaluate 
if 
.
Evaluate
Tap to reveal answer
To evaluate, simply plug in 
for 
:
Remembering the order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution.
To evaluate, simply plug in
Remembering the order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution.
← Didn't Know|Knew It →
Evaluate 
if 
.
Evaluate
Tap to reveal answer
To solve, simply plug in 
for 
:
Remembering the order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution. Also recall that multiplying two negative numbers together leads to a positive product; this is also true when you square a negative number.
From here we can reduce the fraction by factoring out a four from both the numerator and the denominator.
To solve, simply plug in
Remembering the order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution. Also recall that multiplying two negative numbers together leads to a positive product; this is also true when you square a negative number.
From here we can reduce the fraction by factoring out a four from both the numerator and the denominator.
← Didn't Know|Knew It →
Evaluate 
if 
.
Evaluate
Tap to reveal answer
To evaluate, simply plug in 
for 
:
Remembering the order of operations we are able to solve this problem. The order of operations is parentheses, exponents, multiplication, division, addition, subtraction.
To evaluate, simply plug in
Remembering the order of operations we are able to solve this problem. The order of operations is parentheses, exponents, multiplication, division, addition, subtraction.
← Didn't Know|Knew It →
Evaluate 
if 
.
Evaluate
Tap to reveal answer
To evaluate, simply plug in 
for 
:
Recall that we must simplify the exponents before we are able to add the numerator and divide by the denominator.
From here we can reduce the fraction by factoring out a two from both the numerator and the denominator.
To evaluate, simply plug in
Recall that we must simplify the exponents before we are able to add the numerator and divide by the denominator.
From here we can reduce the fraction by factoring out a two from both the numerator and the denominator.
← Didn't Know|Knew It →
Evaluate 
if 
.
Evaluate
Tap to reveal answer
To solve, simply plug in 
for 
:
According to the order of operations we must simplify the exponents first. Then we will multiply the necessary terms and finally we will add and subtract the terms as specified.
To solve, simply plug in
According to the order of operations we must simplify the exponents first. Then we will multiply the necessary terms and finally we will add and subtract the terms as specified.
← Didn't Know|Knew It →
Evaluate 
if 
.
Evaluate
Tap to reveal answer
To solve, simply plug in 
for 
:
First we must simplify the exponents. The we will multiply each of the two terms in the numerator. After that, we can add the terms in denominator and subtract the terms in the numerator.
Sutracting the terms on top gives:
.
We can simplify this fraction by factoring out a sixteen from both the numerator and denominator.
To solve, simply plug in
First we must simplify the exponents. The we will multiply each of the two terms in the numerator. After that, we can add the terms in denominator and subtract the terms in the numerator.
Sutracting the terms on top gives:
We can simplify this fraction by factoring out a sixteen from both the numerator and denominator.
← Didn't Know|Knew It →
If √(ab) = 8, and _a_2 = b, what is a?
If √(ab) = 8, and _a_2 = b, what is a?
Tap to reveal answer
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
If we plug in _a_2 for b in the radical expression, we get √(_a_3) = 8. This can be rewritten as a_3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Find the product of and .
Find the product of
Tap to reveal answer
Solve the first equation for .
Solve the second equation for .
The final step is to multiply and .
Solve the first equation for
Solve the second equation for
The final step is to multiply
← Didn't Know|Knew It →
Evaluate the following rational expression, if :
Evaluate the following rational expression, if
Tap to reveal answer
To evaluate, simply plug in the number for :
Remembering to use order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution.
To evaluate, simply plug in the number
Remembering to use order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final solution.
← Didn't Know|Knew It →
If , find .
If
Tap to reveal answer
To solve, simply plug in for :
Remembering to use the correct order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final answer.
First do the multiplication that is in the numerator.
Now do the subtraction in the denominator.
To solve, simply plug in
Remembering to use the correct order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at our final answer.
First do the multiplication that is in the numerator.
Now do the subtraction in the denominator.
← Didn't Know|Knew It →
Find if .
Find
Tap to reveal answer
To solve, simply plug in for :
Remembering to use the correct order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at the final solution.
Also recall that when a negative number is squared it becomes a positive number. This is also true when we multiply two negative numbers together.
To solve, simply plug in
Remembering to use the correct order of operations (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) we arrive at the final solution.
Also recall that when a negative number is squared it becomes a positive number. This is also true when we multiply two negative numbers together.
← Didn't Know|Knew It →