Numerical Approximation - GRE Quantitative Reasoning
Card 0 of 40
For which values of p is

convergent?
For which values of p is
convergent?
We can solve this problem quite simply with the integral test. We know that if

converges, then our series converges.
We can rewrite the integral as

and then use our formula for the antiderivative of power functions to get that the integral equals
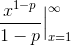 .
.
We know that this only goes to zero if 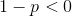 . Subtracting p from both sides, we get
. Subtracting p from both sides, we get
 .
.
We can solve this problem quite simply with the integral test. We know that if
converges, then our series converges.
We can rewrite the integral as
and then use our formula for the antiderivative of power functions to get that the integral equals
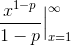
We know that this only goes to zero if 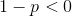

Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx =S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361760/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.4)*(-8.23995)=-1.0987](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361762/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx=S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361739/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.7)*(72.79378)=16.9852](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361741/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx =S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361742/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.2)*(10.5840)=0.7056](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361744/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx\approx S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361736/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.9)*(2.3081)=0.6924](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361757/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369004/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.5)*(0.86027754)=0.4301](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369006/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369007/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.1)*(28.786699)=2.8787](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361699/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx =T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361690/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.4)*(83.89553)=33.5582](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361706/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/368964/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.1)*(11.7257431)=1.1726](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361709/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Evaluate  using the Trapezoidal Rule, with n = 2.
using the Trapezoidal Rule, with n = 2.
Evaluate 
-
n = 2 indicates 2 equal subdivisions. In this case, they are from 0 to 1, and from 1 to 2.
-
Trapezoidal Rule is: ![\int_{a}^{b} f(x)dx \approx \left [ b-a\right ]\left [ \frac{f(a)+f(b)}{2}\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/724677/gif.latex)
-
For n = 2: ![\int_{0}^2 x^{x^{2}} dx \approx [1-0]\left [ \frac{f(0)+f(1)}{2} \right ]+ [2-1]\left [ \frac{f(1)+f(2)}{2} \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/724678/gif.latex)
-
Simplifying: ![\int_{0}^2 x^{x^{2}} dx \approx [1]\left [ \frac{0+1}{2} \right ]+ [1]\left [ \frac{1+16}{2} \right ] = \frac{1}{2}+\frac{17}{2} = \frac{18}{2} = 9.](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/724679/gif.latex)
-
n = 2 indicates 2 equal subdivisions. In this case, they are from 0 to 1, and from 1 to 2.
-
Trapezoidal Rule is:
-
For n = 2:
-
Simplifying:
Compare your answer with the correct one above
For which values of p is

convergent?
For which values of p is
convergent?
We can solve this problem quite simply with the integral test. We know that if

converges, then our series converges.
We can rewrite the integral as

and then use our formula for the antiderivative of power functions to get that the integral equals
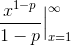 .
.
We know that this only goes to zero if 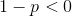 . Subtracting p from both sides, we get
. Subtracting p from both sides, we get
 .
.
We can solve this problem quite simply with the integral test. We know that if
converges, then our series converges.
We can rewrite the integral as
and then use our formula for the antiderivative of power functions to get that the integral equals
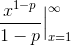
We know that this only goes to zero if 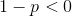

Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx =S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361760/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.4)*(-8.23995)=-1.0987](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361762/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx=S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361739/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.7)*(72.79378)=16.9852](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361741/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx =S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361742/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.2)*(10.5840)=0.7056](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361744/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using Simpson's rule with  subintervals.
subintervals.
Solve the integral
using Simpson's rule with 
Simpson's rule is solved using the formula
![\int_{a}^{b}f(x))dx\approx S_{2m}=\frac{1}{3}(\frac{b-a}{2n})\left [ f(0)+4f(1)+2f(2)+...+2f(m-2)+4f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361736/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  therefore
therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.9)*(2.3081)=0.6924](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361757/gif.latex)
Simpson's rule is solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369004/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.5)*(0.86027754)=0.4301](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369006/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/369007/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.1)*(28.786699)=2.8787](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361699/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx =T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361690/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.4)*(83.89553)=33.5582](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361706/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Solve the integral

using the trapezoidal approximation with  subintervals.
subintervals.
Solve the integral
using the trapezoidal approximation with 
Trapezoidal approximations are solved using the formula
![\int_{a}^{b}f(x))dx\approx T_{n}=(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/368964/gif.latex)
where  is the number of subintervals and
is the number of subintervals and  is the function evaluated at the midpoint.
is the function evaluated at the midpoint.
For this problem,  .
.
The value of each approximation term is below.

The sum of all the approximation terms is  , therefore
, therefore
![(\frac{b-a}{2n})\left [ f(0)+2f(1)+...+f(m-1)+f(m) \right ]=(0.1)*(11.7257431)=1.1726](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/361709/gif.latex)
Trapezoidal approximations are solved using the formula
where 

For this problem, 
The value of each approximation term is below.

The sum of all the approximation terms is 
Compare your answer with the correct one above
Evaluate  using the Trapezoidal Rule, with n = 2.
using the Trapezoidal Rule, with n = 2.
Evaluate 
-
n = 2 indicates 2 equal subdivisions. In this case, they are from 0 to 1, and from 1 to 2.
-
Trapezoidal Rule is: ![\int_{a}^{b} f(x)dx \approx \left [ b-a\right ]\left [ \frac{f(a)+f(b)}{2}\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/724677/gif.latex)
-
For n = 2: ![\int_{0}^2 x^{x^{2}} dx \approx [1-0]\left [ \frac{f(0)+f(1)}{2} \right ]+ [2-1]\left [ \frac{f(1)+f(2)}{2} \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/724678/gif.latex)
-
Simplifying: ![\int_{0}^2 x^{x^{2}} dx \approx [1]\left [ \frac{0+1}{2} \right ]+ [1]\left [ \frac{1+16}{2} \right ] = \frac{1}{2}+\frac{17}{2} = \frac{18}{2} = 9.](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/724679/gif.latex)
-
n = 2 indicates 2 equal subdivisions. In this case, they are from 0 to 1, and from 1 to 2.
-
Trapezoidal Rule is:
-
For n = 2:
-
Simplifying:
Compare your answer with the correct one above