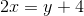GRE Quantitative Reasoning - Calculus

Using the information below, determine the equation of the hyperbola.

Foci: and

Eccentricity:

$\small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{12}=1$

$\small \small \small \small \small \small \small \frac{(x-8)^{2}}{4} - \frac{(y-5)^{2}}{12}=1$

$\small \small \small \small \small \small \small \frac{(x-5)^{2}}{12} - \frac{(y-8)^{2}}{4}=1$

$\small \small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{16}=1$

$\small \small \small \small \small \small \small \small \frac{(x-8)^{2}}{12} - \frac{(y-5)^{2}}{16}=1$

Explanation

General Information for Hyperbola:

Equation for horizontal transverse hyperbola:

$\small \frac{(x-h)^{2}}{a^{2}} - \frac{(y-k)^{2}}{b^{2}}=1$

Distance between foci =

Distance between vertices =

Eccentricity =

$\small a^{2}+b^{2}=c^{2}$

Center: (h, k)

First determine the value of c. Since we know the distance between the two foci is 8, we can set that equal to .

$\small 8=2c$

$\small \small c= 4$

Next, use the eccentricity equation and the value of the eccentricity provided in the question to determine the value of a.

Eccentricity = $\small \small \small \small c/a=2$

$\small \small \frac{c}{a}=\frac{2}{1}=\frac{4}{a}$

$\small \small 4=2a$

$\small \small a=2$

$\small \small \small a^{2}=4$

Determine the value of $\small b^{2}$

$\small a^{2}+b^{2}=c^{2}$

$\small \small \small 2^{2}+b^{2}=4^{2}$

$\small \small \small b^{2}=12$

Determine the center point to identify the values of h and k. Since the y coordinate of the foci are 8, the center point will be on the same line. Hence, $\small \small k = 8$ .

Since center point is equal distance from both foci, and we know that the distance between the foci is 8, we can conclude that $\small \small h=5$

Center point: $\small \small \small (h, k)= (5, 8 )$

Thus, the equation of the hyperbola is:

$\small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{12}=1$

For which of the following functions can the Maclaurin series representation be expressed in four or fewer non-zero terms?

$f(x)= \frac{x^{5}}{3}+2$

$f(x)= x^{2}+\sqrt{x}+1$

$f(x)=x+3\sin(x)$

$f(x)=\ln|x+3|$

Explanation

Recall the Maclaurin series formula:

$f(x)=\sum_{n=0}^{\infty}\frac{f^n(0)}{n!}x^n$

$=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+...$

Despite being a 5th degree polynomial recall that the Maclaurin series for any polynomial is just the polynomial itself, so this function's Taylor series is identical to itself with two non-zero terms.

The only function that has four or fewer terms is $f(x)= \frac{x^{5}}{3}+2$ as its Maclaurin series is $2+\frac{1}{3}x^5$ .

Using the information below, determine the equation of the hyperbola.

Foci: and

Eccentricity:

$\small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{12}=1$

$\small \small \small \small \small \small \small \frac{(x-8)^{2}}{4} - \frac{(y-5)^{2}}{12}=1$

$\small \small \small \small \small \small \small \frac{(x-5)^{2}}{12} - \frac{(y-8)^{2}}{4}=1$

$\small \small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{16}=1$

$\small \small \small \small \small \small \small \small \frac{(x-8)^{2}}{12} - \frac{(y-5)^{2}}{16}=1$

Explanation

General Information for Hyperbola:

Equation for horizontal transverse hyperbola:

$\small \frac{(x-h)^{2}}{a^{2}} - \frac{(y-k)^{2}}{b^{2}}=1$

Distance between foci =

Distance between vertices =

Eccentricity =

$\small a^{2}+b^{2}=c^{2}$

Center: (h, k)

First determine the value of c. Since we know the distance between the two foci is 8, we can set that equal to .

$\small 8=2c$

$\small \small c= 4$

Next, use the eccentricity equation and the value of the eccentricity provided in the question to determine the value of a.

Eccentricity = $\small \small \small \small c/a=2$

$\small \small \frac{c}{a}=\frac{2}{1}=\frac{4}{a}$

$\small \small 4=2a$

$\small \small a=2$

$\small \small \small a^{2}=4$

Determine the value of $\small b^{2}$

$\small a^{2}+b^{2}=c^{2}$

$\small \small \small 2^{2}+b^{2}=4^{2}$

$\small \small \small b^{2}=12$

Determine the center point to identify the values of h and k. Since the y coordinate of the foci are 8, the center point will be on the same line. Hence, $\small \small k = 8$ .

Since center point is equal distance from both foci, and we know that the distance between the foci is 8, we can conclude that $\small \small h=5$

Center point: $\small \small \small (h, k)= (5, 8 )$

Thus, the equation of the hyperbola is:

$\small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{12}=1$

What is the equation of a line that passes through points and in slope-intercept form?

Explanation

To find the equation of the line, first find the slope using the formula:

$m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

The points that the line passes through are and .

$m = \frac{-2-4}{1-3}$

$m= \frac{-6}{-2}$

Then pick one set of points and place in the form . Either set of points will give you the same equation. Points were used.

$4 = 3\times 3 + b$

Subtract from both sides of the equation.

The equation of the line in slope-intercept form or is

What is the equation of the line (in slope-intercept form) that goes through the points: and ?

$y=\frac {4}{5}x+\frac {12}{5}$

$y=\frac {4}{5}x-\frac {12}{5}$

$y=-\frac {4}{5}x+\frac {12}{5}$

$y=-\frac {4}{5}x-\frac {12}{5}$

Explanation

Step 1: Find the slope between the two points:

$\frac {y_2-y_1}{x_2-x_1}=\frac {8-4}{7-2}=\frac {4}{5}$

Step 2: Write the slope-intercept form:

$y=\frac {4}{5}x+b$

Step 3. Find b. Plug in (x,y) from one of the points:

$4=\frac {4}{5}(2)+b$

$4=\frac {8}{5}+b$

$4-\frac {8}{5}=b$

$\frac {20-8}{5}=b$

$\frac {12}{5}=b$
Step 4: Write out the full equation:

$y=\frac {4}{5}x+\frac {12}{5}$

At what point does the line cross the y-axis?

Explanation

Step 1: Rearrange the terms into the form y=mx+b. Move the to the other side.

Step 2: Move the 4 to the other side.

Step 3: When the line crosses the y-axis, the x value is zero. We will plug in for x and find the y value.

$\rightarrow y=-4$

So, the point where this line crosses the y-axis is

What kind of function is this: $f(x)=\sqrt[3] {x-1}$ ?

Cube-Root Function

Square Function

Cube Function

Rational Function

Explanation

Step 1: Look at the equation.. $\sqrt[3] {x-1}$ . The cube-root outside of the function determines what the answer is..

The function is a cube-root function.

Note:

Square function,
Cube function,
Rational function, $\frac {1}{x}$ (if )

What is the equation of the line (in slope-intercept form) that goes through the points: and ?

$y=\frac {4}{5}x+\frac {12}{5}$

$y=\frac {4}{5}x-\frac {12}{5}$

$y=-\frac {4}{5}x+\frac {12}{5}$

$y=-\frac {4}{5}x-\frac {12}{5}$

Explanation

Step 1: Find the slope between the two points:

$\frac {y_2-y_1}{x_2-x_1}=\frac {8-4}{7-2}=\frac {4}{5}$

Step 2: Write the slope-intercept form:

$y=\frac {4}{5}x+b$

Step 3. Find b. Plug in (x,y) from one of the points:

$4=\frac {4}{5}(2)+b$

$4=\frac {8}{5}+b$

$4-\frac {8}{5}=b$

$\frac {20-8}{5}=b$

$\frac {12}{5}=b$
Step 4: Write out the full equation:

$y=\frac {4}{5}x+\frac {12}{5}$

What is the equation of a line that passes through points and in slope-intercept form?

Explanation

To find the equation of the line, first find the slope using the formula:

$m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

The points that the line passes through are and .

$m = \frac{-2-4}{1-3}$

$m= \frac{-6}{-2}$

Then pick one set of points and place in the form . Either set of points will give you the same equation. Points were used.

$4 = 3\times 3 + b$

Subtract from both sides of the equation.

The equation of the line in slope-intercept form or is

Find the slope of a line that passes through and

$m=\frac{1}{2}$

$m=-\frac{1}{2}$

Explanation

The formula for slope is:

$m = \frac{y_{2} - y_{1}}{x_{2} -x_{1}}$

$m = \frac{5-(-1)}{6-3}$

$m = \frac{5+1}{6-3}$

$m = \frac{6}{3}$

Calculus

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation