Algebraic Concepts - HiSET
Card 0 of 232
Identify the coefficients in the following formula:

Identify the coefficients in the following formula:
Generally speaking, in an equation a coefficient is a constant by which a variable is multiplied. For example,  and
and  are coefficients in the following equation:
are coefficients in the following equation:

In our equation, the following numbers are coefficients:

Generally speaking, in an equation a coefficient is a constant by which a variable is multiplied. For example, 

In our equation, the following numbers are coefficients:
Compare your answer with the correct one above
What is the coefficient of the second highest term in the expression:  ?
?
What is the coefficient of the second highest term in the expression: 
Step 1: Rearrange the terms from highest power to lowest power.
We will get:  .
.
Step 2: We count the second term from starting from the left since it is the second highest term in the rearranged expression.
Step 3: Isolate the term.
The second term is 
Step 4: Find the coefficient. The coefficient of a term is considered as the number before any variables. In this case, the coefficient is  .
.
So, the answer is  .
.
Step 1: Rearrange the terms from highest power to lowest power.
We will get: 
Step 2: We count the second term from starting from the left since it is the second highest term in the rearranged expression.
Step 3: Isolate the term.
The second term is
Step 4: Find the coefficient. The coefficient of a term is considered as the number before any variables. In this case, the coefficient is 
So, the answer is 
Compare your answer with the correct one above
Identify the terms in the following equation:

Identify the terms in the following equation:
In an equation, a term is a single number or a variable. in our equation we have the following terms:

In an equation, a term is a single number or a variable. in our equation we have the following terms:
Compare your answer with the correct one above
How many terms are in the following expression:  ?
?
How many terms are in the following expression: 
Step 1: We need to separate and arrange the terms in the jumbled expression given to us in the question..
We will separate the terms by the exponent value.
For  , there is only one term:
, there is only one term: 
For  , there are no terms.
, there are no terms.
For  , there is two terms:
, there is two terms: 
For  , there are two terms:
, there are two terms: 
For  , there are two terms:
, there are two terms: 
For  , there is only one term:
, there is only one term: 
For  , there are two terms:
, there are two terms: 
For  , there are three terms:
, there are three terms: 
There are four constant terms: 
Step 2: We will now add up the coefficients in each designation of terms. This will give us the answer.

Step 1: We need to separate and arrange the terms in the jumbled expression given to us in the question..
We will separate the terms by the exponent value.
For 
For 
For 
For 
For 
For 
For 
For 
There are four constant terms:
Step 2: We will now add up the coefficients in each designation of terms. This will give us the answer.
Compare your answer with the correct one above
Simplify the polynomial
 .
.
How many terms does the simplified form have?
Simplify the polynomial

How many terms does the simplified form have?
Arrange and combine like terms (those with the same variable) as follows:




Since each term now has a different exponent for the variable, no further combining is possible. The simplified form has four terms.
Arrange and combine like terms (those with the same variable) as follows:
Since each term now has a different exponent for the variable, no further combining is possible. The simplified form has four terms.
Compare your answer with the correct one above
Add these two expressions together:  and
and  .
.
Add these two expressions together: 

Step 1: Add the terms based on their similarities...
 and
and  becomes
becomes  .
.
 and
and  becomes
becomes  .
.
 and
and  becomes
becomes 
Step 2: Combine all the terms after "becomes" in step 1...
We add and get:  .
.
Step 1: Add the terms based on their similarities...








Step 2: Combine all the terms after "becomes" in step 1...
We add and get: 
Compare your answer with the correct one above
Subtract  and
and  .
.
Subtract 

Step 1: Subtract these terms by separating by exponents...





Step 2: Add all the simplified terms together...

Step 1: Subtract these terms by separating by exponents...
Step 2: Add all the simplified terms together...
Compare your answer with the correct one above
Solve for  :
:

Solve for 
To solve for  in a literal equation, use the properties of algebra to isolate
in a literal equation, use the properties of algebra to isolate  on one side, just as if you were solving a regular equation.
on one side, just as if you were solving a regular equation.

Subtract 20 from both sides:


Divide both sides by  :
:

 ,
,
the correct response.
To solve for 

Subtract 20 from both sides:
Divide both sides by 

the correct response.
Compare your answer with the correct one above
Add or subtract: 
Add or subtract:
Step 1: Find the Least Common Denominator of these fraction. We will list out multiples of each denominator until we find a common number for all three fractions...



The smallest common denominator is  .
.
Step 2: Since the denominator is  , we will convert all denominators to
, we will convert all denominators to  .
.
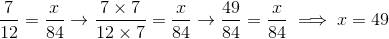


Step 3: Add up all the values of x...

Step 4: The result from step  is the numerator and
is the numerator and  is the denominator. We will put these together.
is the denominator. We will put these together.
Final Answer: 
Step 1: Find the Least Common Denominator of these fraction. We will list out multiples of each denominator until we find a common number for all three fractions...
The smallest common denominator is 
Step 2: Since the denominator is 

Step 3: Add up all the values of x...
Step 4: The result from step 

Final Answer:
Compare your answer with the correct one above
A quadratic function  has two zeroes, 3 and 7. What could this function be?
has two zeroes, 3 and 7. What could this function be?
A quadratic function 
A polynomial function with zeroes 3 and 7 has as its factors  and
and  . The function is given to be quadratic, so this function is
. The function is given to be quadratic, so this function is
 .
.
Apply the FOIL method to rewrite the polynomial:


Collect like terms:
 ,
,
the correct choice.
A polynomial function with zeroes 3 and 7 has as its factors 


Apply the FOIL method to rewrite the polynomial:
Collect like terms:

the correct choice.
Compare your answer with the correct one above

What is 25% of  ?
?
What is 25% of 
Solve for  in the equation
in the equation
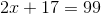
by isolating  on the left side. Do this by reversing the operations in the reverse of the order of operations.
on the left side. Do this by reversing the operations in the reverse of the order of operations.
First, subtract 17 from both sides:

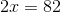
Now, divide both sides by 2:


One way to find 25% of this value is to multiply 41 by 25 and divide by 100:
 ,
,
the correct choice.
Solve for 
by isolating 
First, subtract 17 from both sides:
Now, divide both sides by 2:
One way to find 25% of this value is to multiply 41 by 25 and divide by 100:

the correct choice.
Compare your answer with the correct one above
What is the vertex of the following quadratic polynomial?

What is the vertex of the following quadratic polynomial?
Given a quadratic function

the vertex will always be
 .
.
Thus, since our function is

 ,
,  , and
, and  .
.
We plug these variables into the formula to get the vertex as


 .
.
Hence, the vertex of

is
 .
.
Given a quadratic function
the vertex will always be

Thus, since our function is



We plug these variables into the formula to get the vertex as

Hence, the vertex of
is

Compare your answer with the correct one above
Which of the following expressions represents the discriminant of the following polynomial?

Which of the following expressions represents the discriminant of the following polynomial?
The discriminant of a quadratic polynomial

is given by
 .
.
Thus, since our quadratic polynomial is
 ,
,
 ,
,  , and
, and  .
.
Plugging these values into the discriminant equation, we find that the discriminant is
 .
.
The discriminant of a quadratic polynomial
is given by

Thus, since our quadratic polynomial is




Plugging these values into the discriminant equation, we find that the discriminant is

Compare your answer with the correct one above
Give the nature of the solution set of the equation

Give the nature of the solution set of the equation
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form

This can be done by adding 17 to both sides:


The key to determining the nature of the solution set is to examine the discriminant
 . Setting
. Setting  , the value of the discriminant is
, the value of the discriminant is

This value is negative. Consequently, the solution set comprises two imaginary numbers.
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
This can be done by adding 17 to both sides:
The key to determining the nature of the solution set is to examine the discriminant


This value is negative. Consequently, the solution set comprises two imaginary numbers.
Compare your answer with the correct one above
Which of the following polynomial equations has exactly one solution?
Which of the following polynomial equations has exactly one solution?
A polynomial equation of the form

has one and only one (real) solution if and only if its discriminant is equal to zero - that is, if its coefficients satisfy the equation

In each of the choices,  and
and  , so it suffices to determine the value of
, so it suffices to determine the value of  which satisfies this equation. Substituting, we get
which satisfies this equation. Substituting, we get


Solve for  by first adding 400 to both sides:
by first adding 400 to both sides:


Take the square root of both sides:

The choice that matches this value of  is the equation
is the equation

A polynomial equation of the form
has one and only one (real) solution if and only if its discriminant is equal to zero - that is, if its coefficients satisfy the equation
In each of the choices, 


Solve for 
Take the square root of both sides:
The choice that matches this value of 
Compare your answer with the correct one above
Give the nature of the solution set of the equation

Give the nature of the solution set of the equation
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form

To accomplish this, first, multiply the binomials on the left using the FOIL technique:



Collect like terms:

Now, subtract 18 from both sides:


The key to determining the nature of the solution set is to examine the discriminant  . Setting
. Setting  , the value of the discriminant is
, the value of the discriminant is

The discriminant is a positive number, so there are two real solutions. Since 73 is not a perfect square, the solutions are irrational.
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
To accomplish this, first, multiply the binomials on the left using the FOIL technique:
Collect like terms:
Now, subtract 18 from both sides:
The key to determining the nature of the solution set is to examine the discriminant 

The discriminant is a positive number, so there are two real solutions. Since 73 is not a perfect square, the solutions are irrational.
Compare your answer with the correct one above
Give the nature of the solution set of the equation

Give the nature of the solution set of the equation
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form

To accomplish this, first, multiply the binomials on the left using the FOIL technique:



Collect like terms:

Add 6 to both sides:


The key to determining the nature of the solution set is to examine the discriminant  . Setting
. Setting  , the value of the discriminant is
, the value of the discriminant is

The discriminant is a positive number; furthermore, it is a perfect square, being equal to the square of 11. Therefore, the solution set comprises two rational solutions.
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
To accomplish this, first, multiply the binomials on the left using the FOIL technique:
Collect like terms:
Add 6 to both sides:
The key to determining the nature of the solution set is to examine the discriminant 

The discriminant is a positive number; furthermore, it is a perfect square, being equal to the square of 11. Therefore, the solution set comprises two rational solutions.
Compare your answer with the correct one above
Give the nature of the solution set of the equation
 .
.
Give the nature of the solution set of the equation

To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form

This can be done by simply switching the first and second terms:


The key to determining the nature of the solution set is to examine the discriminant  . Setting
. Setting  , the value of the discriminant is
, the value of the discriminant is

The discriminant has a negative value. It follows that the solution set comprises two imaginary values.
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
This can be done by simply switching the first and second terms:
The key to determining the nature of the solution set is to examine the discriminant 

The discriminant has a negative value. It follows that the solution set comprises two imaginary values.
Compare your answer with the correct one above
Which of the following polynomial equations has exactly one solution?
Which of the following polynomial equations has exactly one solution?
A polynomial equation of the standard form

has one and only one (real) solution if and only if its discriminant is equal to zero - that is, if its coefficients satisfy the equation

Each of the choices can be rewritten in standard form by subtracting the term on the right from both sides. One of the choices can be rewritten as follows:



By similar reasoning, the other four choices can be written:




In each of the five standard forms,  and
and  , so it is necessary to determine the value of
, so it is necessary to determine the value of  that produces a zero discriminant. Substituting accordingly:
that produces a zero discriminant. Substituting accordingly:



Add 900 to both sides and take the square root:



Of the five standard forms,

fits this condition. This is the standard form of the equation
 ,
,
the correct choice.
A polynomial equation of the standard form
has one and only one (real) solution if and only if its discriminant is equal to zero - that is, if its coefficients satisfy the equation
Each of the choices can be rewritten in standard form by subtracting the term on the right from both sides. One of the choices can be rewritten as follows:
By similar reasoning, the other four choices can be written:
In each of the five standard forms, 


Add 900 to both sides and take the square root:
Of the five standard forms,
fits this condition. This is the standard form of the equation

the correct choice.
Compare your answer with the correct one above
Give the nature of the solution set of the equation

Give the nature of the solution set of the equation
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form

To accomplish this, first, multiply the binomials on the left using the FOIL technique:



Collect like terms:

Now, add 18 to both sides:


The key to determining the nature of the solution set is to examine the discriminant  . Setting
. Setting  , the value of the discriminant is
, the value of the discriminant is

This discriminant is negative. Consequently, the solution set comprises two imaginary numbers.
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
To accomplish this, first, multiply the binomials on the left using the FOIL technique:
Collect like terms:
Now, add 18 to both sides:
The key to determining the nature of the solution set is to examine the discriminant 

This discriminant is negative. Consequently, the solution set comprises two imaginary numbers.
Compare your answer with the correct one above