ISEE Upper Level Quantitative Reasoning - Geometry

Trapezoid

The above diagram depicts trapezoid . Which is the greater quantity?

(a) $m \angle T + m \angle P$

(b) $m \angle R + m \angle A$

(a) and (b) are equal.

(a) is greater.

(b) is greater.

It is impossible to tell from the information given.

Explanation

$\overline{TR} \parallel \overline{PA}$ ; $\angle T$ and $\angle P$ are same-side interior angles, as are $\angle R$ and $\angle A$ .

The Same-Side Interior Angles Theorem states that if two parallel lines are crossed by a transversal, then the sum of the measures of a pair of same-side interior angles is always $180^{\circ}$ .

Therefore, $m \angle T + m \angle P = 180= m \angle R + m \angle A$ , making the two quantities equal.

Trapezoid

In the above figure, $\overline{XY}$ is the midsegment of Trapezoid . What percent of Trapezoid has been shaded in?

$37 \frac{1}{2} %$

$33 \frac{1}{3} %$

Explanation

Midsegment $\overline{XY}$ divides Trapezoid into two trapezoids of the same height, which we will call ; the length of the midsegment is half sum of the lengths of the bases:

$XY = \frac{1}{2} (12 + 36) = \frac{1}{2} \cdot 48= 24$

The area of a trapezoid is one half multiplied by its height multiplied by the sum of the lengths of its bases. Therefore, the area of Trapezoid - the shaded trapezoid - is

$\frac{1}{2} \cdot h \cdot (TR+XY ) = \frac{1}{2} \cdot h \cdot (12+24) = \frac{1}{2} \cdot 36 \cdot h = 18 h$

The area of Trapezoid is

$\frac{1}{2} \cdot 2 h \cdot (TR+AP) = \frac{1}{2} \cdot 2 \cdot h \cdot (12+36) = \frac{1}{2} \cdot 2 \cdot 48 \cdot h = 48 h$

The percent of Trapezoid that is shaded in is

$\frac{18h}{48h} \cdot 100 % = \frac{18}{48} \cdot 100 % = 37 \frac{1}{2} %$

In a certain quadrilateral, three of the angles are $65^{\circ}$ , $120^{\circ}$ , and $34^{\circ}$ . What is the measure of the fourth angle?

$141^{\circ}$

$139^{\circ}$

$219^{\circ}$

$41^{\circ}$

$29^{\circ}$

Explanation

A quadrilateral has four angles totalling $360^{\circ}$ . So, first add up the three angles given. The sum is $219^{\circ}$ . Then, subtract that from 360. This gives you the missing angle, which is $141^{\circ}$ .

A cube has a side length of , what is the volume of the cube?

Explanation

A cube has a side length of , what is the volume of the cube?

To find the volume of a cube, use the following formula:

$V_{cube}=s^3$

Plug in our known side length and solve

$V_{cube}=(9mm)^3=729mm^3$

Making our answer:

The circumferences of eight circles form an arithmetic sequence. The smallest circle has radius two inches; the second smallest circle has radius five inches. Give the radius of the largest circle.

1 foot, 11 inches

2 feet

2 feet, 1 inch

4 feet 2 inches

3 feet 10 inches

Explanation

The circumference of a circle can be determined by multiplying its radius by $2 \pi$ , so the circumferences of the two smallest circles are

$C_{1} = 2 \cdot 2 \pi = 4 \pi$

and

$C_{2} = 2 \cdot 5 \pi = 10 \pi$

The circumferences form an arithmetic sequence with common difference

$C_{2}- C_{1}= 10 \pi - 4 \pi = 6 \pi$

The circumference of a circle can therefore be found using the formula

$C_{n} = C_{1} + (n-1)d$

where $C_{1} = 4 \pi$ and $d = 6 \pi$ ; we are looking for that of the th smallest circle, so

$C_{8} = 4 \pi + (8-1)6 \pi$

$= 4 \pi + 7 \cdot 6 \pi$

$= 4 \pi + 42 \pi$

$= 46 \pi$

Since the radius of a circle is the circumference of the circle divided by $2 \pi$ , the radius of this eighth circle is

$r = \frac{46 \pi}{2 \pi} = 23$ inches, or 1 foot 11 inches.

Parallelogram

Note: Figure NOT drawn to scale

The above figure shows Rhombus .

Which is the greater quantity?

(a)

(b)

(a) and (b) are equal

It is impossible to determine which is greater from the information given

(b) is the greater quantity

(a) is the greater quantity

Explanation

The opposite sides of a parallelogram - a rhombus included - are congruent, so

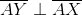
Also, Quadrilateral form a rectangle; since $\overline{AX} || \overline{CY}$ and $\overline{AY} \perp \overline{CY}$ , it follows that $\overline{AY} \perp \overline{AX}$ , and, similarly, $\overline{XC} \perp \overline{CY}$ . Therefore, , and

Which is the greater quantity?

(a) The sidelength of a square with area square inches.

(b) The sidelength of a square with perimeter inches.

(a) is greater.

(b) is greater.

(a) and (b) are equal.

It is impossible to tell which is greater from the information given.

Explanation

The sidelength of a square is the square root of its area and one-fourth of its perimeter, so:

(a) A square with area square inches has sidelength $\sqrt{225} = 15$ inches.

(b) A square with perimeter inches has sidelength $50 \div 4 = 12.5$ inches.

(a) is the greater quantity.

The lengths of the sides of ten squares form an arithmetic sequence. One side of the smallest square measures sixty centimeters; one side of the second-smallest square measures one meter.

Give the area of the largest square, rounded to the nearest square meter.

18 square meters

16 square meters

20 square meters

22 square meters

24 square meters