ISEE Upper Level Quantitative Reasoning - Quadrilaterals

In a certain quadrilateral, three of the angles are $65^{\circ}$ , $120^{\circ}$ , and $34^{\circ}$ . What is the measure of the fourth angle?

$141^{\circ}$

$139^{\circ}$

$219^{\circ}$

$41^{\circ}$

$29^{\circ}$

Explanation

A quadrilateral has four angles totalling $360^{\circ}$ . So, first add up the three angles given. The sum is $219^{\circ}$ . Then, subtract that from 360. This gives you the missing angle, which is $141^{\circ}$ .

A rectangle has perimeter 140 inches and area 1,200 square inches. Which is the greater quantity?

(A) The length of a diagonal of the rectangle.

(B) 4 feet

(A) is greater

(B) is greater

(A) and (B) are equal

It is impossible to determine which is greater from the information given

Explanation

Let and be the dimensions of the rectangle. Then

and, subsequently,

Since the product of the length and width is the area, we are looking for two numbers whose sum is 70 and whose product is 1,200; through trial and error, they are found to be 30 and 40. We can assign either to be and the other to be since the result is the same.

The length of a diagonal of the rectangle can be found by applying the Pythagorean Theorem:

$D = \sqrt{L^{2}+ W^{2}}$

$D = \sqrt{30^{2}+ 40^{2}} = \sqrt{900+1,600} = \sqrt{2,500} = 50$

A diagonal is 50 inches long; since 4 feet are equivalent to 48 inches, (A) is the greater quantity.

The area of a rectangle is 4,480 square inches. Its width is 70% of its length.

What is its perimeter?

$272 \textrm{ in}$

$224\textrm{ in}$

$284\textrm{ in}$

$302\textrm{ in}$

It is impossible to determine the area from the given information.

Explanation

If the width of the rectangle is 70% of the length, then

The area is the product of the length and width:

$L \cdot 0.70 L = 4,480$

$0.70 L ^{2}= 4,480$

$0.70 L ^{2} \div 0.70 = 4,480\div 0.70$

$L ^{2} = 6,400$

$L = \sqrt{6,400} = 80$

$W = 0.70 L = 0.70 \cdot 80 = 56$

The perimeter is therefore

$P = 2L + 2W = 2 \cdot 80 + 2 \cdot 56 = 160 + 112 = 272$ inches.

A rectangle is two feet longer than it is wide; its perimeter is 11 feet. What is its area in square inches?

$945 \textrm{ in}^{2}$

$513 \textrm{ in}^{2}$

$4,212 \textrm{ in}^{2}$

$3,780 \textrm{ in}^{2}$

It is impossible to determine the area from the information given

Explanation

The length of the rectangle is 2 feet, or 24 inches, greater than the width, so, if is the width in inches, is the length in inches.

The perimeter of the rectangle is 11 feet, or $11 \times 12= 132$ inches. The perimeter, in terms of length and width, is , so we can set up the equation:

$4 W \div 4 =84 \div 4$

The width is 21 inches, and the length is 45 inches. The area is their product:

$21\times 45 = 945$ square inches.

Which quantity is greater?

(a) The perimeter of a square with area 10,000 square centimeters

(b) The perimeter of a rectangle with area 8,000 square centimeters

It is impossible to tell from the information given

(a) and (b) are equal

(b) is greater

(a) is greater

Explanation

A square with area 10,000 square centimeters has sidelength $\sqrt{10,000} = 100$ centimeters, and perimeter $4 \times 100 = 400$ centimeters.

Not enough information is given about the rectangle with area 8,000 square centimeters to determine its perimeter. For example, if its dimensions are 100 centimeters by 80 centimeters, its perimeter is centimeters. If the dimensions are 200 centimeters by 40 centimeters, its perimeter is centimeters. Both cases are consistent with the conditions of the problem, yet one makes (a) greater and one makes (b) greater.

Parallelogram

Note: Figure NOT drawn to scale

The above figure shows Rhombus .

Which is the greater quantity?

(a)

(b)

(a) and (b) are equal

It is impossible to determine which is greater from the information given

(b) is the greater quantity

(a) is the greater quantity

Explanation

The opposite sides of a parallelogram - a rhombus included - are congruent, so

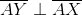
Also, Quadrilateral form a rectangle; since $\overline{AX} || \overline{CY}$ and $\overline{AY} \perp \overline{CY}$ , it follows that $\overline{AY} \perp \overline{AX}$ , and, similarly, $\overline{XC} \perp \overline{CY}$ . Therefore, , and

Trapezoid

In the above figure, $\overline{XY}$ is the midsegment of Trapezoid . Give the ratio of the area of Trapezoid to that of Trapezoid .

33 to 19

10 to 3

13 to 6

20 to 13

Explanation

Midsegment $\overline{XY}$ divides Trapezoid into two trapezoids of the same height, which we will call ; the length of the midsegment is half sum of the lengths of the bases:

$XY = \frac{1}{2} (12 + 40) = \frac{1}{2} \cdot 52 = 26$ .

The area of a trapezoid is one half multiplied by its height multiplied by the sum of the lengths of its bases. Therefore, the area of Trapezoid is

$\frac{1}{2} \cdot h \cdot (TR+XY ) = \frac{1}{2} \cdot h \cdot (12+26 ) = \frac{1}{2} \cdot 38 \cdot h = 19 h$

The area of Trapezoid is

$\frac{1}{2} \cdot h \cdot (XY +AP) = \frac{1}{2} \cdot h \cdot ( 26+40 ) = \frac{1}{2} \cdot 66 \cdot h = 33 h$

The ratio of the areas is

$\frac{33 h}{19h} = \frac{33}{19}$ , or 33 to 19.

Trapezoid

Figure NOT drawn to scale.

In the above figure, $\overline{XY}$ is the midsegment of isosceles Trapezoid . Also, $TX = \frac{1}{2} XY$ .

What is the perimeter of Trapezoid ?

Explanation

The length of the midsegment of a trapezoid is half sum of the lengths of the bases, so

$XY = \frac{1}{2} (12 + 40) = \frac{1}{2} \cdot 52 = 26$ .

Also, by definition, since Trapezoid is isosceles, . The midsegment divides both legs of Trapezoid into congruent segments; combining these facts:

$TX = XP = \frac{1}{2} TP = \frac{1}{2} RA = RY = YA$

$TX = \frac{1}{2} XY = \frac{1}{2} \cdot 26 = 13$ .

, so the perimeter of Trapezoid is

Trapezoid

In the above figure, $\overline{XY}$ is the midsegment of Trapezoid . What percent of Trapezoid has been shaded in?

$37 \frac{1}{2} %$

$33 \frac{1}{3} %$

Explanation

Midsegment $\overline{XY}$ divides Trapezoid into two trapezoids of the same height, which we will call ; the length of the midsegment is half sum of the lengths of the bases:

$XY = \frac{1}{2} (12 + 36) = \frac{1}{2} \cdot 48= 24$

The area of a trapezoid is one half multiplied by its height multiplied by the sum of the lengths of its bases. Therefore, the area of Trapezoid - the shaded trapezoid - is