Calculus I — Derivatives - Math
Card 1 of 344
When  , what is the concavity of the graph of
, what is the concavity of the graph of  ?
?
When 

Tap to reveal answer
To find the concavity, we need to look at the first and second derivatives at the given point.
To take the first derivative of this equation, use the power rule. The power rule says that we lower the exponent of each variable by one and multiply that number by the original exponent:

Simplify:

Remember that anything to the zero power is equal to one.


The first derivative tells us if the function is increasing or decreasing. Plug in the given point,  , to see if the result is positive (i.e. increasing) or negative (i.e. decreasing).
, to see if the result is positive (i.e. increasing) or negative (i.e. decreasing).


Therefore the function is increasing.
To find out if the function is convex, we need to look at the second derivative evaluated at the same point,  , and check if it is positive or negative.
, and check if it is positive or negative.
We're going to treat  as
as  since anything to the zero power is equal to one.
since anything to the zero power is equal to one.

Notice that  since anything times zero is zero.
since anything times zero is zero.


Plug in our given value:


Since the second derivative is positive, the function is convex.
Therefore, we are looking at a graph that is both increasing and convex at our given point.
To find the concavity, we need to look at the first and second derivatives at the given point.
To take the first derivative of this equation, use the power rule. The power rule says that we lower the exponent of each variable by one and multiply that number by the original exponent:
Simplify:
Remember that anything to the zero power is equal to one.
The first derivative tells us if the function is increasing or decreasing. Plug in the given point, 
Therefore the function is increasing.
To find out if the function is convex, we need to look at the second derivative evaluated at the same point, 
We're going to treat 

Notice that 
Plug in our given value:
Since the second derivative is positive, the function is convex.
Therefore, we are looking at a graph that is both increasing and convex at our given point.
← Didn't Know|Knew It →
At the point  , is
, is  increasing or decreasing, and is it concave or convex?
increasing or decreasing, and is it concave or convex?
At the point 

Tap to reveal answer
To find out if the function is increasing or decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.



Anything to the zero power is one.


Now we plug in our given value and find out if the result is positive or negative. If it is positive, the function is increasing. If it is negative, the function is decreasing.




Therefore, the function is decreasing.
To find out if it is concave or convex, look at the second derivative. If the result is positive, it is convex. If it is negative, then it is concave.
To find the second derivative, we repeat the process using  as our expression.
as our expression.
We're going to treat  as
as  .
.

Notice that  since anything times zero is zero.
since anything times zero is zero.


As stated before, anything to the zero power is one.

Since we get a positive constant, it doesn't matter where we look on the graph, as our second derivative will always be positive. That means that this graph is going to be convex at our given point.
Therefore, the function is decreasing and convex at our given point.
To find out if the function is increasing or decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
Anything to the zero power is one.
Now we plug in our given value and find out if the result is positive or negative. If it is positive, the function is increasing. If it is negative, the function is decreasing.
Therefore, the function is decreasing.
To find out if it is concave or convex, look at the second derivative. If the result is positive, it is convex. If it is negative, then it is concave.
To find the second derivative, we repeat the process using 
We're going to treat 

Notice that 
As stated before, anything to the zero power is one.
Since we get a positive constant, it doesn't matter where we look on the graph, as our second derivative will always be positive. That means that this graph is going to be convex at our given point.
Therefore, the function is decreasing and convex at our given point.
← Didn't Know|Knew It →
At the point  , is the function
, is the function  increasing or decreasing, concave or convex?
increasing or decreasing, concave or convex?
At the point 

Tap to reveal answer
First, let's find out if the graph is increasing or decreasing. For that, we need the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat  as
as  since anything to the zero power is one.
since anything to the zero power is one.

Notice that  since anything times zero is zero.
since anything times zero is zero.


Plug in our given point for  . If the result is positive, the function is increasing. If the result is negative, the function is decreasing.
. If the result is positive, the function is increasing. If the result is negative, the function is decreasing.



Our result is negative, therefore the function is decreasing.
To find the concavity, look at the second derivative. If the function is positive at our given point, it is concave. If the function is negative, it is convex.
To find the second derivative we repeat the process, but using  as our expression.
as our expression.



As you can see, our second derivative is a constant. It doesn't matter what point we plug in for  ; our output will always be negative. Therefore our graph will always be convex.
; our output will always be negative. Therefore our graph will always be convex.
Combine our two pieces of information to see that at the given point, the graph is decreasing and convex.
First, let's find out if the graph is increasing or decreasing. For that, we need the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
Plug in our given point for 
Our result is negative, therefore the function is decreasing.
To find the concavity, look at the second derivative. If the function is positive at our given point, it is concave. If the function is negative, it is convex.
To find the second derivative we repeat the process, but using 
As you can see, our second derivative is a constant. It doesn't matter what point we plug in for 
Combine our two pieces of information to see that at the given point, the graph is decreasing and convex.
← Didn't Know|Knew It →
At the point where  , is
, is  increasing or decreasing, and is it concave up or down?
increasing or decreasing, and is it concave up or down?
At the point where 

Tap to reveal answer
To find if the equation is increasing or decreasing, we need to look at the first derivative. If our result is positive at  , then the function is increasing. If it is negative, then the function is decreasing.
, then the function is increasing. If it is negative, then the function is decreasing.
To find the first derivative for this problem, we can use the power rule. The power rule states that we lower the exponent of each of the variables by one and multiply by that original exponent.


Remember that anything to the zero power is one.


Plug in our given value.




Is it positive? Yes. Then it is increasing.
To find the concavity, we need to look at the second derivative. If it is positive, then the function is concave up. If it is negative, then the function is concave down.
Repeat the process we used for the first derivative, but use  as our expression.
as our expression.
For this problem, we're going to say that  since, as stated before, anything to the zero power is one.
since, as stated before, anything to the zero power is one.

Notice that  as anything times zero is zero.
as anything times zero is zero.



As you can see, there is no place for a variable here. It doesn't matter what point we look at, the answer will always be positive. Therefore this graph is always concave up.
This means that at our given point, the graph is increasing and concave up.
To find if the equation is increasing or decreasing, we need to look at the first derivative. If our result is positive at 
To find the first derivative for this problem, we can use the power rule. The power rule states that we lower the exponent of each of the variables by one and multiply by that original exponent.
Remember that anything to the zero power is one.
Plug in our given value.
Is it positive? Yes. Then it is increasing.
To find the concavity, we need to look at the second derivative. If it is positive, then the function is concave up. If it is negative, then the function is concave down.
Repeat the process we used for the first derivative, but use 
For this problem, we're going to say that 
Notice that 
As you can see, there is no place for a variable here. It doesn't matter what point we look at, the answer will always be positive. Therefore this graph is always concave up.
This means that at our given point, the graph is increasing and concave up.
← Didn't Know|Knew It →
Let  . What is the largest interval of x for which f(x) is concave upward?
. What is the largest interval of x for which f(x) is concave upward?
Let 
Tap to reveal answer
This question asks us to examine the concavity of the function  . We will need to find the second derivative in order to determine where the function is concave upward and downward. Whenever its second derivative is positive, a function is concave upward.
. We will need to find the second derivative in order to determine where the function is concave upward and downward. Whenever its second derivative is positive, a function is concave upward.
Let us begin by finding the first derivative of f(x). We will need to use the Product Rule. According to the Product Rule, if  , then
, then  . In this particular problem, let
. In this particular problem, let  and
and  . Applying the Product rule, we get
. Applying the Product rule, we get
![f'(x)=\left ($\frac{\mathrm{d}$ }{\mathrm{d} x}[x] \right )\cdot $e^{x^2}$+\left ($\frac{\mathrm{d}$ }{\mathrm{d} $x}[e^{ x^2}$] \right )\cdot x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/103021/gif.latex)
![f'(x)=1\cdot $e^{x^2}$+\left ($\frac{\mathrm{d}$ }{\mathrm{d} $x}[e^{ x^2}$] \right )\cdot x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/110466/gif.latex)
In order to evaluate the derivative of  , we will need to invoke the Chain Rule. According to the Chain Rule, the derivative of a function in the form
, we will need to invoke the Chain Rule. According to the Chain Rule, the derivative of a function in the form  is given by
is given by  . In finding the derivative of
. In finding the derivative of  , we will let
, we will let  and
and  .
.
![$\frac{\mathrm{d}$ }{\mathrm{d} $x}[e^{x^2}$$]=e^{x^2}$\cdot $\frac{\mathrm{d}$ }{\mathrm{d} $x}[x^2$]=2x\cdot $e^{x^2}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/103025/gif.latex)
We can now finish finding the derivative of the original function.
![f'(x)=1\cdot $e^{x^2}$+\left($\frac{\mathrm{d}$ }{\mathrm{d} $x}[e^{ x^2}$] \right)\cdot x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/116585/gif.latex)

To summarize, the first derivative of the funciton  is
is  .
.
We need the second derivative in order to examine the concavity of f(x), so we will differentiate one more time. Once again, we will have to use the Product Rule in conjunction with the Chain Rule.
![f''(x)=\frac{\mathrm{d}$ }{\mathrm{d} x}[f'(x)]=\left ($\frac{\mathrm{d}$ }{\mathrm{d} $x}[e^{x^2}$] \right $)\cdot(2x^2$+1)+\left ($\frac{\mathrm{d}$ }{\mathrm{d} x} [ $2x^2$+1] \right ) \cdot $e^{x^2 }$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/116586/gif.latex)


In order to find where f(x) is concave upward, we must find where f''(x) > 0.

In order to solve this inequality, we can divide both sides by  . Notice that
. Notice that  is always positive (because e raised to any power will be positive); this means that when we divide both sides of the inequality by
is always positive (because e raised to any power will be positive); this means that when we divide both sides of the inequality by  , we won't have to flip the sign. (If we divide an inequality by a negative quantity, the sign flips.)
, we won't have to flip the sign. (If we divide an inequality by a negative quantity, the sign flips.)
Dividing both sides of the inequality by  gives us
gives us

When solving inequalities with polynomials, we often need to factor.

Notice now that the expression  will always be positive, because the smallest value it can take on is 3, when x is equal to zero. Thus, we can safely divide both sides of the inequality by
will always be positive, because the smallest value it can take on is 3, when x is equal to zero. Thus, we can safely divide both sides of the inequality by  without having to change the direction of the sign. This leaves us with the inequality
without having to change the direction of the sign. This leaves us with the inequality
 , which clearly only holds when
, which clearly only holds when  .
.
Thus, the second derivative of f''(x) will be positive (and f(x) will be concave up) only when  . To represent this using interval notation (as the answer choices specify) we would write this as
. To represent this using interval notation (as the answer choices specify) we would write this as  .
.
The answer is  .
.
This question asks us to examine the concavity of the function 
Let us begin by finding the first derivative of f(x). We will need to use the Product Rule. According to the Product Rule, if 



In order to evaluate the derivative of 





We can now finish finding the derivative of the original function.
To summarize, the first derivative of the funciton 

We need the second derivative in order to examine the concavity of f(x), so we will differentiate one more time. Once again, we will have to use the Product Rule in conjunction with the Chain Rule.
In order to find where f(x) is concave upward, we must find where f''(x) > 0.
In order to solve this inequality, we can divide both sides by 


Dividing both sides of the inequality by 
When solving inequalities with polynomials, we often need to factor.
Notice now that the expression 



Thus, the second derivative of f''(x) will be positive (and f(x) will be concave up) only when 

The answer is 
← Didn't Know|Knew It →
Find the derivative of the following function:

Find the derivative of the following function:
Tap to reveal answer
Since this function is a polynomial, we take the derivative of each term separately.
From the power rule, the derivative of

is simply

We can rewrite  as
as

and using the power rule again, we get a derivative of
 or
or 
So the answer is

Since this function is a polynomial, we take the derivative of each term separately.
From the power rule, the derivative of
is simply
We can rewrite 
and using the power rule again, we get a derivative of

So the answer is
← Didn't Know|Knew It →
Which of the following best represents  ?
?
Which of the following best represents 
Tap to reveal answer
The question is just asking for the Quotient Rule formula.
Recall the Quotient Rule is the bottom function times the derivative of the top minus the top function times the derivative of the bottom all divided by the bottom function squared.
Given,

the bottom function is  and the top function is
and the top function is  . This makes the bottom derivative
. This makes the bottom derivative  and the top derivative
and the top derivative  .
.
Substituting these into the Quotient Rule formula resulting in the following.

The question is just asking for the Quotient Rule formula.
Recall the Quotient Rule is the bottom function times the derivative of the top minus the top function times the derivative of the bottom all divided by the bottom function squared.
Given,
the bottom function is 



Substituting these into the Quotient Rule formula resulting in the following.
← Didn't Know|Knew It →
What is 
What is
Tap to reveal answer
The chain rule is "first times the derivative of the second plus second times derivative of the first".
In this case, that means  .
.
The chain rule is "first times the derivative of the second plus second times derivative of the first".
In this case, that means 
← Didn't Know|Knew It →
What is the first derivative of  ?
?
What is the first derivative of 
Tap to reveal answer
Since we're adding terms, we take the derivative of each part separately. For  , we can use the power rule, which states that we multiply the variable by the current exponent and then lower the exponent by one. For sine, we use our trigonometric derivative rules.
, we can use the power rule, which states that we multiply the variable by the current exponent and then lower the exponent by one. For sine, we use our trigonometric derivative rules.
Remember,  .
.


Since we're adding terms, we take the derivative of each part separately. For 
Remember, 
← Didn't Know|Knew It →
What is the second derivative of  ?
?
What is the second derivative of 
Tap to reveal answer
To find the second derivative, we need to start by finding the first one.
Since we're adding terms, we take the derivative of each part separately. For  , we can use the power rule, which states that we multiply the variable by the current exponent and then lower the exponent by one. For sine, we use our trigonometric derivative rules.
, we can use the power rule, which states that we multiply the variable by the current exponent and then lower the exponent by one. For sine, we use our trigonometric derivative rules.
Remember,  .
.


Now we repeat the process, but using  as our equation.
as our equation.



To find the second derivative, we need to start by finding the first one.
Since we're adding terms, we take the derivative of each part separately. For 
Remember, 
Now we repeat the process, but using 
← Didn't Know|Knew It →
An ellipse is represented by the following equation:

What is the slope of the curve at the point (3,2)?
An ellipse is represented by the following equation:
What is the slope of the curve at the point (3,2)?
Tap to reveal answer
It would be difficult to differentiate this equation by isolating 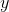 . Luckily, we don't have to. Use
. Luckily, we don't have to. Use  to represent the derivative of
to represent the derivative of  with respect to
with respect to  and follow the chain rule.
and follow the chain rule.
(Remember, 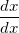 is the derivative of
is the derivative of  with respect to
with respect to  , although it usually doesn't get written out because it is equal to 1. We'll write it out this time so you can see how implicit differentiation works.)
, although it usually doesn't get written out because it is equal to 1. We'll write it out this time so you can see how implicit differentiation works.)




Now we need to isolate  by first putting all of these terms on the same side:
by first putting all of these terms on the same side:

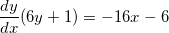

This is the equation for the derivative at any point on the curve. By substituting in (3, 2) from the original question, we can find the slope at that particular point:

It would be difficult to differentiate this equation by isolating 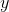



(Remember, 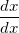


Now we need to isolate 
This is the equation for the derivative at any point on the curve. By substituting in (3, 2) from the original question, we can find the slope at that particular point:
← Didn't Know|Knew It →
If  , what is
, what is  ?
?
If 

Tap to reveal answer
For this problem, we can use the power rule. The power rule states that we multiply each variable by its current exponent and then lower that exponent by one.

Simplify.

Anything to the zero power is one, so  .
.
Therefore,  .
.
For this problem, we can use the power rule. The power rule states that we multiply each variable by its current exponent and then lower that exponent by one.
Simplify.
Anything to the zero power is one, so 
Therefore, 
← Didn't Know|Knew It →
Find the derivative of the following function:

Find the derivative of the following function:
Tap to reveal answer
We use the power rule on each term of the function.
The first term

becomes
 .
.
The second term

becomes
 .
.
The final term, 7, is a constant, so its derivative is simply zero.
We use the power rule on each term of the function.
The first term
becomes

The second term
becomes

The final term, 7, is a constant, so its derivative is simply zero.
← Didn't Know|Knew It →
Give the average rate of change of the function  on the interval
on the interval ![[3,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/125515/gif.latex) .
.
Give the average rate of change of the function 
![[3,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/125515/gif.latex)
Tap to reveal answer
The average rate of change of  on interval
on interval ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/109706/gif.latex) is
is

Substitute:

The average rate of change of 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/109706/gif.latex)
Substitute:
← Didn't Know|Knew It →
What is the derivative of  ?
?
What is the derivative of 
Tap to reveal answer
To get  , we can use the power rule.
, we can use the power rule.
Since the exponent of the  is
is  , as
, as  , we lower the exponent by one and then multiply the coefficient by that original exponent:
, we lower the exponent by one and then multiply the coefficient by that original exponent:


Anything to the  power is
power is  .
.


To get 
Since the exponent of the 


Anything to the 

← Didn't Know|Knew It →
What is the derivative of  ?
?
What is the derivative of 
Tap to reveal answer
To solve this problem, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.


Remember that anything to the zero power is one.


To solve this problem, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
Remember that anything to the zero power is one.
← Didn't Know|Knew It →
What is the derivative of  ?
?
What is the derivative of 
Tap to reveal answer
To solve this problem, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
We're going to treat  as
as  , as anything to the zero power is one.
, as anything to the zero power is one.
That means this problem will look like this:

Notice that  , as anything times zero is zero.
, as anything times zero is zero.


Remember, anything to the zero power is one.


To solve this problem, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
We're going to treat 

That means this problem will look like this:
Notice that 
Remember, anything to the zero power is one.
← Didn't Know|Knew It →
What is the derivative of  ?
?
What is the derivative of 
Tap to reveal answer
To solve this problem, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
We're going to treat  as
as  , as anything to the zero power is one.
, as anything to the zero power is one.

Notice that  , as anything times zero is zero.
, as anything times zero is zero.



To solve this problem, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
We're going to treat 

Notice that 
← Didn't Know|Knew It →
Tap to reveal answer
To solve this equation, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat  as
as  since anything to the zero power is one.
since anything to the zero power is one.
)
Notice that  since anything times zero is zero.
since anything times zero is zero.



To solve this equation, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat 

Notice that 
← Didn't Know|Knew It →
What is the derivative of  ?
?
What is the derivative of 
Tap to reveal answer
To solve this equation, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat  as
as  since anything to the zero power is one.
since anything to the zero power is one.

Notice that  since anything times zero is zero.
since anything times zero is zero.
That leaves us with  .
.
Simplify.


As stated earlier, anything to the zero power is one, leaving us with:

To solve this equation, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat 

Notice that 
That leaves us with 
Simplify.
As stated earlier, anything to the zero power is one, leaving us with:
← Didn't Know|Knew It →
