Functions and Graphs - Math
Card 0 of 24
Solve:


Solve:
Use substution to solve this problem:
 becomes
becomes  and then is substituted into the second equation. Then solve for
and then is substituted into the second equation. Then solve for  :
:
 , so
, so  and
and  to give the solution
to give the solution  .
.
Use substution to solve this problem:







Compare your answer with the correct one above
Solve for the  - and
- and  - intercepts:
- intercepts:

Solve for the 

To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the 


To solve for the 


Compare your answer with the correct one above
Write 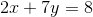 in slope-intercept form.
in slope-intercept form.
Write 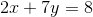
Slope-intercept form is  .
.



Slope-intercept form is 
Compare your answer with the correct one above
List the transformations that have been enacted upon the following equation:
![f(x)=4[6(x-3)]^{4}-7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106187/gif.latex)
List the transformations that have been enacted upon the following equation:
Since the equation given in the question is based off of the parent function  , we can write the general form for transformations like this:
, we can write the general form for transformations like this:
![g(x) = a[b(x-c)^{4}]+d](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106188/gif.latex)
 determines the vertical stretch or compression factor.
determines the vertical stretch or compression factor.
- If
 is greater than 1, the function has been vertically stretched (expanded) by a factor of
is greater than 1, the function has been vertically stretched (expanded) by a factor of  .
.
- If
 is between 0 and 1, the function has been vertically compressed by a factor of
is between 0 and 1, the function has been vertically compressed by a factor of  .
.
In this case,  is 4, so the function has been vertically stretched by a factor of 4.
is 4, so the function has been vertically stretched by a factor of 4.
 determines the horizontal stretch or compression factor.
determines the horizontal stretch or compression factor.
- If
 is greater than 1, the function has been horizontally compressed by a factor of
is greater than 1, the function has been horizontally compressed by a factor of  .
.
- If
 is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of  .
.
In this case,  is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
 determines the horizontal translation.
determines the horizontal translation.
- If
 is positive, the function was translated
is positive, the function was translated  units right.
units right.
- If
 is negative, the function was translated
is negative, the function was translated  units left.
units left.
In this case,  is 3, so the function was translated 3 units right.
is 3, so the function was translated 3 units right.
 determines the vertical translation.
determines the vertical translation.
- If
 is positive, the function was translated
is positive, the function was translated  units up.
units up.
- If
 is negative, the function was translated
is negative, the function was translated  units down.
units down.
In this case,  is -7, so the function was translated 7 units down.
is -7, so the function was translated 7 units down.
Since the equation given in the question is based off of the parent function 

- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of
.
In this case, 

- If
is greater than 1, the function has been horizontally compressed by a factor of
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
.
In this case, 

- If
is positive, the function was translated
units right.
- If
is negative, the function was translated
units left.
In this case, 

- If
is positive, the function was translated
units up.
- If
is negative, the function was translated
units down.
In this case, 
Compare your answer with the correct one above
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain  .
.
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
Compare your answer with the correct one above
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain
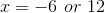
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
Compare your answer with the correct one above
Solve:


Solve:
Use substution to solve this problem:
 becomes
becomes  and then is substituted into the second equation. Then solve for
and then is substituted into the second equation. Then solve for  :
:
 , so
, so  and
and  to give the solution
to give the solution  .
.
Use substution to solve this problem:







Compare your answer with the correct one above
Solve for the  - and
- and  - intercepts:
- intercepts:

Solve for the 

To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the 


To solve for the 


Compare your answer with the correct one above
Write 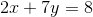 in slope-intercept form.
in slope-intercept form.
Write 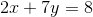
Slope-intercept form is  .
.



Slope-intercept form is 
Compare your answer with the correct one above
List the transformations that have been enacted upon the following equation:
![f(x)=4[6(x-3)]^{4}-7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106187/gif.latex)
List the transformations that have been enacted upon the following equation:
Since the equation given in the question is based off of the parent function  , we can write the general form for transformations like this:
, we can write the general form for transformations like this:
![g(x) = a[b(x-c)^{4}]+d](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106188/gif.latex)
 determines the vertical stretch or compression factor.
determines the vertical stretch or compression factor.
- If
 is greater than 1, the function has been vertically stretched (expanded) by a factor of
is greater than 1, the function has been vertically stretched (expanded) by a factor of  .
.
- If
 is between 0 and 1, the function has been vertically compressed by a factor of
is between 0 and 1, the function has been vertically compressed by a factor of  .
.
In this case,  is 4, so the function has been vertically stretched by a factor of 4.
is 4, so the function has been vertically stretched by a factor of 4.
 determines the horizontal stretch or compression factor.
determines the horizontal stretch or compression factor.
- If
 is greater than 1, the function has been horizontally compressed by a factor of
is greater than 1, the function has been horizontally compressed by a factor of  .
.
- If
 is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of  .
.
In this case,  is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
 determines the horizontal translation.
determines the horizontal translation.
- If
 is positive, the function was translated
is positive, the function was translated  units right.
units right.
- If
 is negative, the function was translated
is negative, the function was translated  units left.
units left.
In this case,  is 3, so the function was translated 3 units right.
is 3, so the function was translated 3 units right.
 determines the vertical translation.
determines the vertical translation.
- If
 is positive, the function was translated
is positive, the function was translated  units up.
units up.
- If
 is negative, the function was translated
is negative, the function was translated  units down.
units down.
In this case,  is -7, so the function was translated 7 units down.
is -7, so the function was translated 7 units down.
Since the equation given in the question is based off of the parent function 

- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of
.
In this case, 

- If
is greater than 1, the function has been horizontally compressed by a factor of
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
.
In this case, 

- If
is positive, the function was translated
units right.
- If
is negative, the function was translated
units left.
In this case, 

- If
is positive, the function was translated
units up.
- If
is negative, the function was translated
units down.
In this case, 
Compare your answer with the correct one above
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain  .
.
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
Compare your answer with the correct one above
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain
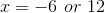
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
Compare your answer with the correct one above
Solve:


Solve:
Use substution to solve this problem:
 becomes
becomes  and then is substituted into the second equation. Then solve for
and then is substituted into the second equation. Then solve for  :
:
 , so
, so  and
and  to give the solution
to give the solution  .
.
Use substution to solve this problem:







Compare your answer with the correct one above
Solve for the  - and
- and  - intercepts:
- intercepts:

Solve for the 

To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the 


To solve for the 


Compare your answer with the correct one above
Write 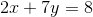 in slope-intercept form.
in slope-intercept form.
Write 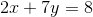
Slope-intercept form is  .
.



Slope-intercept form is 
Compare your answer with the correct one above
List the transformations that have been enacted upon the following equation:
![f(x)=4[6(x-3)]^{4}-7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106187/gif.latex)
List the transformations that have been enacted upon the following equation:
Since the equation given in the question is based off of the parent function  , we can write the general form for transformations like this:
, we can write the general form for transformations like this:
![g(x) = a[b(x-c)^{4}]+d](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106188/gif.latex)
 determines the vertical stretch or compression factor.
determines the vertical stretch or compression factor.
- If
 is greater than 1, the function has been vertically stretched (expanded) by a factor of
is greater than 1, the function has been vertically stretched (expanded) by a factor of  .
.
- If
 is between 0 and 1, the function has been vertically compressed by a factor of
is between 0 and 1, the function has been vertically compressed by a factor of  .
.
In this case,  is 4, so the function has been vertically stretched by a factor of 4.
is 4, so the function has been vertically stretched by a factor of 4.
 determines the horizontal stretch or compression factor.
determines the horizontal stretch or compression factor.
- If
 is greater than 1, the function has been horizontally compressed by a factor of
is greater than 1, the function has been horizontally compressed by a factor of  .
.
- If
 is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of  .
.
In this case,  is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
 determines the horizontal translation.
determines the horizontal translation.
- If
 is positive, the function was translated
is positive, the function was translated  units right.
units right.
- If
 is negative, the function was translated
is negative, the function was translated  units left.
units left.
In this case,  is 3, so the function was translated 3 units right.
is 3, so the function was translated 3 units right.
 determines the vertical translation.
determines the vertical translation.
- If
 is positive, the function was translated
is positive, the function was translated  units up.
units up.
- If
 is negative, the function was translated
is negative, the function was translated  units down.
units down.
In this case,  is -7, so the function was translated 7 units down.
is -7, so the function was translated 7 units down.
Since the equation given in the question is based off of the parent function 

- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of
.
In this case, 

- If
is greater than 1, the function has been horizontally compressed by a factor of
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
.
In this case, 

- If
is positive, the function was translated
units right.
- If
is negative, the function was translated
units left.
In this case, 

- If
is positive, the function was translated
units up.
- If
is negative, the function was translated
units down.
In this case, 
Compare your answer with the correct one above
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain  .
.
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
Compare your answer with the correct one above
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain
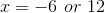
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
Compare your answer with the correct one above
Solve:


Solve:
Use substution to solve this problem:
 becomes
becomes  and then is substituted into the second equation. Then solve for
and then is substituted into the second equation. Then solve for  :
:
 , so
, so  and
and  to give the solution
to give the solution  .
.
Use substution to solve this problem:







Compare your answer with the correct one above
Solve for the  - and
- and  - intercepts:
- intercepts:

Solve for the 

To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the 


To solve for the 


Compare your answer with the correct one above