Polynomials - Math
Card 1 of 116
Factor the polynomial if the expression is equal to zero when  .
.

Factor the polynomial if the expression is equal to zero when 
Tap to reveal answer
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression  fits the description of the zeroes.
fits the description of the zeroes.
Now we need to check the answer.


We are able to get back to the original expression, meaning that the answer is  .
.
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression 
Now we need to check the answer.
We are able to get back to the original expression, meaning that the answer is 
← Didn't Know|Knew It →
A polyomial with leading term  has 5 and 7 as roots; 7 is a double root. What is this polynomial?
has 5 and 7 as roots; 7 is a double root. What is this polynomial?
A polyomial with leading term 
Tap to reveal answer
Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is  . To put this in expanded form:
. To put this in expanded form:






Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is 
← Didn't Know|Knew It →
A polyomial with leading term  has 6 as a triple root. What is this polynomial?
has 6 as a triple root. What is this polynomial?
A polyomial with leading term 
Tap to reveal answer
Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is  , which we can expland using the cube of a binomial pattern.
, which we can expland using the cube of a binomial pattern.


Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is 
← Didn't Know|Knew It →
What are the solutions to  ?
?
What are the solutions to 
Tap to reveal answer
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of  such that the output will be zero. Thus, we first factor the equation.
such that the output will be zero. Thus, we first factor the equation.

Then, we are looking for the values where each of these factors are equal to zero.
 implies
implies 
and  implies
implies 
Thus, these are our solutions.
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of 
Then, we are looking for the values where each of these factors are equal to zero.

and 
Thus, these are our solutions.
← Didn't Know|Knew It →
Simplify the following polynomial function:

Simplify the following polynomial function:
Tap to reveal answer
First, multiply the outside term with each term within the parentheses:


Rearranging the polynomial into fractional form, we get:

First, multiply the outside term with each term within the parentheses:
Rearranging the polynomial into fractional form, we get:
← Didn't Know|Knew It →
Simplify the following polynomial:

Simplify the following polynomial:
Tap to reveal answer
To simplify the polynomial, begin by combining like terms:


To simplify the polynomial, begin by combining like terms:
← Didn't Know|Knew It →
Find the zeros of the following polynomial:

Find the zeros of the following polynomial:
Tap to reveal answer
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:

Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for  , we're hoping that the equation ends up equaling zero. Let's see if
, we're hoping that the equation ends up equaling zero. Let's see if  is a zero:
is a zero:
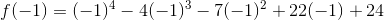


Since the function equals zero when  is
is  , one of the factors of the polynomial is
, one of the factors of the polynomial is  . This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.
. This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.



Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try  :
:
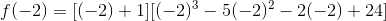

When we factor using synthetic substitution for  , we get the following result:
, we get the following result:

Using our quadratic factoring rules, we can factor completely:

Thus, the zeroes of  are
are 
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
← Didn't Know|Knew It →
Simplify the following polynomial function:

Simplify the following polynomial function:
Tap to reveal answer
First, multiply the outside term with each term within the parentheses:


Rearranging the polynomial into fractional form, we get:

First, multiply the outside term with each term within the parentheses:
Rearranging the polynomial into fractional form, we get:
← Didn't Know|Knew It →
Simplify the following polynomial:

Simplify the following polynomial:
Tap to reveal answer
To simplify the polynomial, begin by combining like terms:


To simplify the polynomial, begin by combining like terms:
← Didn't Know|Knew It →
Factor the polynomial if the expression is equal to zero when  .
.

Factor the polynomial if the expression is equal to zero when 
Tap to reveal answer
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression  fits the description of the zeroes.
fits the description of the zeroes.
Now we need to check the answer.


We are able to get back to the original expression, meaning that the answer is  .
.
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression 
Now we need to check the answer.
We are able to get back to the original expression, meaning that the answer is 
← Didn't Know|Knew It →
A polyomial with leading term  has 5 and 7 as roots; 7 is a double root. What is this polynomial?
has 5 and 7 as roots; 7 is a double root. What is this polynomial?
A polyomial with leading term 
Tap to reveal answer
Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is  . To put this in expanded form:
. To put this in expanded form:






Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is 
← Didn't Know|Knew It →
A polyomial with leading term  has 6 as a triple root. What is this polynomial?
has 6 as a triple root. What is this polynomial?
A polyomial with leading term 
Tap to reveal answer
Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is  , which we can expland using the cube of a binomial pattern.
, which we can expland using the cube of a binomial pattern.


Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is 
← Didn't Know|Knew It →
What are the solutions to  ?
?
What are the solutions to 
Tap to reveal answer
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of  such that the output will be zero. Thus, we first factor the equation.
such that the output will be zero. Thus, we first factor the equation.

Then, we are looking for the values where each of these factors are equal to zero.
 implies
implies 
and  implies
implies 
Thus, these are our solutions.
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of 
Then, we are looking for the values where each of these factors are equal to zero.

and 
Thus, these are our solutions.
← Didn't Know|Knew It →
Find the zeros of the following polynomial:

Find the zeros of the following polynomial:
Tap to reveal answer
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:

Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for  , we're hoping that the equation ends up equaling zero. Let's see if
, we're hoping that the equation ends up equaling zero. Let's see if  is a zero:
is a zero:
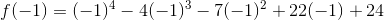


Since the function equals zero when  is
is  , one of the factors of the polynomial is
, one of the factors of the polynomial is  . This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.
. This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.



Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try  :
:
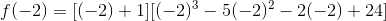

When we factor using synthetic substitution for  , we get the following result:
, we get the following result:

Using our quadratic factoring rules, we can factor completely:

Thus, the zeroes of  are
are 
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
← Didn't Know|Knew It →
Factor the polynomial if the expression is equal to zero when  .
.

Factor the polynomial if the expression is equal to zero when 
Tap to reveal answer
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression  fits the description of the zeroes.
fits the description of the zeroes.
Now we need to check the answer.


We are able to get back to the original expression, meaning that the answer is  .
.
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression 
Now we need to check the answer.
We are able to get back to the original expression, meaning that the answer is 
← Didn't Know|Knew It →
A polyomial with leading term  has 5 and 7 as roots; 7 is a double root. What is this polynomial?
has 5 and 7 as roots; 7 is a double root. What is this polynomial?
A polyomial with leading term 
Tap to reveal answer
Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is  . To put this in expanded form:
. To put this in expanded form:






Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is 
← Didn't Know|Knew It →
A polyomial with leading term  has 6 as a triple root. What is this polynomial?
has 6 as a triple root. What is this polynomial?
A polyomial with leading term 
Tap to reveal answer
Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is  , which we can expland using the cube of a binomial pattern.
, which we can expland using the cube of a binomial pattern.


Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is 
← Didn't Know|Knew It →
What are the solutions to  ?
?
What are the solutions to 
Tap to reveal answer
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of  such that the output will be zero. Thus, we first factor the equation.
such that the output will be zero. Thus, we first factor the equation.

Then, we are looking for the values where each of these factors are equal to zero.
 implies
implies 
and  implies
implies 
Thus, these are our solutions.
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of 
Then, we are looking for the values where each of these factors are equal to zero.

and 
Thus, these are our solutions.
← Didn't Know|Knew It →
Simplify the following polynomial function:

Simplify the following polynomial function:
Tap to reveal answer
First, multiply the outside term with each term within the parentheses:


Rearranging the polynomial into fractional form, we get:

First, multiply the outside term with each term within the parentheses:
Rearranging the polynomial into fractional form, we get:
← Didn't Know|Knew It →
Simplify the following polynomial:

Simplify the following polynomial:
Tap to reveal answer
To simplify the polynomial, begin by combining like terms:


To simplify the polynomial, begin by combining like terms:
← Didn't Know|Knew It →