How to find the length of the side of a right triangle - Math
Card 1 of 228
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
Tap to reveal answer
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
← Didn't Know|Knew It →
Given a right triangle with a leg length of 2 and a hypotenuse length of √8, find the length of the other leg, x.

Given a right triangle with a leg length of 2 and a hypotenuse length of √8, find the length of the other leg, x.

Tap to reveal answer
Using Pythagorean Theorem, we can solve for the length of leg x:
_x_2 + 22 = (√8)2 = 8
Now we solve for x:
_x_2 + 4 = 8
_x_2 = 8 – 4
_x_2 = 4
x = 2
Using Pythagorean Theorem, we can solve for the length of leg x:
_x_2 + 22 = (√8)2 = 8
Now we solve for x:
_x_2 + 4 = 8
_x_2 = 8 – 4
_x_2 = 4
x = 2
← Didn't Know|Knew It →
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
Tap to reveal answer
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
← Didn't Know|Knew It →
Given a right triangle with a leg length of 6 and a hypotenuse length of 10, find the length of the other leg, x.

Given a right triangle with a leg length of 6 and a hypotenuse length of 10, find the length of the other leg, x.

Tap to reveal answer
Using Pythagorean Theorem, we can solve for the length of leg x:
_x_2 + 62 = 102
Now we solve for x:
_x_2 + 36 = 100
_x_2 = 100 – 36
_x_2 = 64
x = 8
Also note that this is proportionally a 3/4/5 right triangle, which is very common. Always look out for a side-to-hypoteneuse ratio of 3/5 or 4/5, or a side-to-side ratio of 3/4, in any right triangle, so that you may solve such triangles rapidly.
Using Pythagorean Theorem, we can solve for the length of leg x:
_x_2 + 62 = 102
Now we solve for x:
_x_2 + 36 = 100
_x_2 = 100 – 36
_x_2 = 64
x = 8
Also note that this is proportionally a 3/4/5 right triangle, which is very common. Always look out for a side-to-hypoteneuse ratio of 3/5 or 4/5, or a side-to-side ratio of 3/4, in any right triangle, so that you may solve such triangles rapidly.
← Didn't Know|Knew It →
A right triangle has one side equal to 5 and its hypotenuse equal to 14. Its third side is equal to:
A right triangle has one side equal to 5 and its hypotenuse equal to 14. Its third side is equal to:
Tap to reveal answer
The Pythagorean Theorem gives us _a_2 + _b_2 = _c_2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides. Here a is equal to 5 and c is equal to 14, so _b_2 = 142 – 52 = 171. Therefore b is equal to the square root of 171 or approximately 13.07.
The Pythagorean Theorem gives us _a_2 + _b_2 = _c_2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides. Here a is equal to 5 and c is equal to 14, so _b_2 = 142 – 52 = 171. Therefore b is equal to the square root of 171 or approximately 13.07.
← Didn't Know|Knew It →
Which of the following could NOT be the lengths of the sides of a right triangle?
Which of the following could NOT be the lengths of the sides of a right triangle?
Tap to reveal answer
We use the Pythagorean Theorem and we calculate that 25 + 49 is not equal to 100.
All of the other answer choices observe the theorem _a_2 + _b_2 = _c_2
We use the Pythagorean Theorem and we calculate that 25 + 49 is not equal to 100.
All of the other answer choices observe the theorem _a_2 + _b_2 = _c_2
← Didn't Know|Knew It →
Which set of sides could make a right triangle?
Which set of sides could make a right triangle?
Tap to reveal answer
By virtue of the Pythagorean Theorem, in a right triangle the sum of the squares of the smaller two sides equals the square of the largest side. Only 9, 12, and 15 fit this rule.
By virtue of the Pythagorean Theorem, in a right triangle the sum of the squares of the smaller two sides equals the square of the largest side. Only 9, 12, and 15 fit this rule.
← Didn't Know|Knew It →
A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.

A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.

Tap to reveal answer
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
← Didn't Know|Knew It →
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
Tap to reveal answer
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
← Didn't Know|Knew It →
In a right triangle a hypotenuse has a length of 8 and leg has a length of 7. What is the length of the third side to the nearest tenth?
In a right triangle a hypotenuse has a length of 8 and leg has a length of 7. What is the length of the third side to the nearest tenth?
Tap to reveal answer
Using the pythagorean theorem, 82=72+x2. Solving for x yields the square root of 15, which is 3.9
Using the pythagorean theorem, 82=72+x2. Solving for x yields the square root of 15, which is 3.9
← Didn't Know|Knew It →
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
Tap to reveal answer
Area= $\frac{1}{2}$times basetimes height
42=\frac{1}{2}$times basetimes 12
42=6times base
base=7
Area= $\frac{1}{2}$times basetimes height
42=\frac{1}{2}$times basetimes 12
42=6times base
base=7
← Didn't Know|Knew It →


If  and
and  , what is the length of
, what is the length of  ?
?

If 


Tap to reveal answer
AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a  triangle, the opposites sides of those angles will be in the ratio
triangle, the opposites sides of those angles will be in the ratio  .
.
Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to  .
.




which also means

AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a 

Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to 
which also means
← Didn't Know|Knew It →
The length of segment $\overline{BD}$ is $\frac{4sqrt{3}$}{3}
Note that triangles ACD and BCD are both special, 30-60-90 right triangles. Looking specifically at triangle ACD, because we know that segment $\overline{AD}$ has a length of 4, we can determine that the length of segment $\overline{CD}$ is 2 using what we know about special right triangles. Then, looking at triangle BCD now, we can use the same rules to determine that segment $\overline{BD}$ has a length of $\frac{4}{sqrt{3}$}
which simplifies to $\frac{4sqrt{3}$}{3}.
The length of segment $\overline{BD}$ is $\frac{4sqrt{3}$}{3}
Note that triangles ACD and BCD are both special, 30-60-90 right triangles. Looking specifically at triangle ACD, because we know that segment $\overline{AD}$ has a length of 4, we can determine that the length of segment $\overline{CD}$ is 2 using what we know about special right triangles. Then, looking at triangle BCD now, we can use the same rules to determine that segment $\overline{BD}$ has a length of $\frac{4}{sqrt{3}$}
which simplifies to $\frac{4sqrt{3}$}{3}.
← Didn't Know|Knew It →
The legs of a right triangle are 8 cm and 11 cm. Rounded to the nearest whole number, what is the length of the hypotenuse?
The legs of a right triangle are 8 cm and 11 cm. Rounded to the nearest whole number, what is the length of the hypotenuse?
Tap to reveal answer
Use the Pythagorean Theorem. The sum of both legs squared equals the hypotenuse squared.
Use the Pythagorean Theorem. The sum of both legs squared equals the hypotenuse squared.
← Didn't Know|Knew It →
![]()
Solve for x.
Solve for x.
Tap to reveal answer
Use the Pythagorean Theorem. Let a = 8 and c = 10 (because it is the hypotenuse)
$a^2$$+x^2$$=c^2$
$8^2$$+x^2$$=10^2$
$64+x^2$=100
$x^2$=100-64=36
x=6
Use the Pythagorean Theorem. Let a = 8 and c = 10 (because it is the hypotenuse)
$a^2$$+x^2$$=c^2$
$8^2$$+x^2$$=10^2$
$64+x^2$=100
$x^2$=100-64=36
x=6
← Didn't Know|Knew It →
Solve for  (rounded to the nearest tenth). Figure not drawn to scale.
(rounded to the nearest tenth). Figure not drawn to scale.
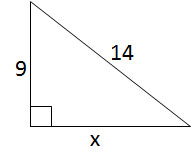
Solve for 

Tap to reveal answer
We will use the Pythagorean Theorem to solve for the missing side length.





We will use the Pythagorean Theorem to solve for the missing side length.
← Didn't Know|Knew It →
A square boxing ring has a perimeter of  feet. When the two boxers are sitting in opposite corners between rounds, how far apart are they?
feet. When the two boxers are sitting in opposite corners between rounds, how far apart are they?
A square boxing ring has a perimeter of 
Tap to reveal answer
Since the perimeter of the ring is  feet and the ring is a square, solve for the length of a single side of the ring by dividing by
feet and the ring is a square, solve for the length of a single side of the ring by dividing by  .
.

The distance between the two boxers in opposing corners is a straight line from any one corner to the other. That straight line forms the hypotenuse of a right triangle whose other two sides are each  feet long (since they are each the sides of the square).
feet long (since they are each the sides of the square).
Solving for the length of the hypotenuse of this right triangle with the pythagorean theorem  provides the distance between the two boxers when they are in opposite corners.
provides the distance between the two boxers when they are in opposite corners.





Since the perimeter of the ring is 

The distance between the two boxers in opposing corners is a straight line from any one corner to the other. That straight line forms the hypotenuse of a right triangle whose other two sides are each 
Solving for the length of the hypotenuse of this right triangle with the pythagorean theorem 
← Didn't Know|Knew It →

 ,
,  ,
,  ,
, 
 .
.
 .
.



 .
.

 .
.
 .
.


 .
.


