How to find the length of the side of of an acute / obtuse isosceles triangle - Math
Card 1 of 40
A triangle has a perimeter of  inches with one side of length
inches with one side of length  inches. If the remaining two sides have lengths in a ratio of
inches. If the remaining two sides have lengths in a ratio of  , what is length of the shortest side of the triangle?
, what is length of the shortest side of the triangle?
A triangle has a perimeter of 


Tap to reveal answer
The answer is  .
.
Since we know that the permieter is 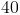 inches and one side is
inches and one side is  inches, it can be determined that the remaining two sides must combine to be
inches, it can be determined that the remaining two sides must combine to be  inches. The ratio of the remaining two sides is
inches. The ratio of the remaining two sides is 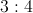 which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation
which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation  , and divide both sides by
, and divide both sides by  which means
which means  . The ratio of the remaining side lengths then becomes
. The ratio of the remaining side lengths then becomes  or
or  . We now know the 3 side lengths are
. We now know the 3 side lengths are 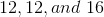 .
.
 is the shortest side and thus the answer.
is the shortest side and thus the answer.
The answer is 
Since we know that the permieter is 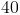


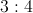





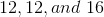

← Didn't Know|Knew It →
Given  such that
such that  ,
,  ,
,  , which of the following statements is true?
, which of the following statements is true?
Given 



Tap to reveal answer
Having three sides of different lengths, this triangle is scalene. In any scalene triangle, the angle with greatest measure is opposite the longest side, and the angle with least measure is opposite the shortest side. Therefore, since  , their opposite angles would be in order from greatest to least measure - that is,
, their opposite angles would be in order from greatest to least measure - that is,  .
.
Having three sides of different lengths, this triangle is scalene. In any scalene triangle, the angle with greatest measure is opposite the longest side, and the angle with least measure is opposite the shortest side. Therefore, since 

← Didn't Know|Knew It →
Find the perimeter of the triangle below.

Find the perimeter of the triangle below.

Tap to reveal answer
Use the Pythagorean Theorem to find the base of the right triangle.




Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.

Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.
← Didn't Know|Knew It →
Find the perimeter of the triangle below.

Find the perimeter of the triangle below.

Tap to reveal answer
Use the Pythagorean Theorem to find the base of the right triangle.




Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.

Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.
← Didn't Know|Knew It →
If a triangle has side lengths of  and
and  , which of the following can be a length of the third side?
, which of the following can be a length of the third side?
If a triangle has side lengths of 

Tap to reveal answer

The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:



The side length of  is the only choice that fits this criteria:
is the only choice that fits this criteria:




The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:
The side length of 
← Didn't Know|Knew It →
If a triangle has side lengths of  and
and  , which of the following could be the length of the third side?
, which of the following could be the length of the third side?
If a triangle has side lengths of 

Tap to reveal answer

The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:



The side length of  is the only choice that fits this criteria:
is the only choice that fits this criteria:




The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:
The side length of 
← Didn't Know|Knew It →
A triangle has sides of lengths 14, 18, and 20. Is the triangle scalene or isosceles?
A triangle has sides of lengths 14, 18, and 20. Is the triangle scalene or isosceles?
Tap to reveal answer
A triangle with three sides of different length is, by definition, scalene.
A triangle with three sides of different length is, by definition, scalene.
← Didn't Know|Knew It →
Given: Regular Pentagon  with center
with center  . Construct segments
. Construct segments  and
and  to form
to form  .
.
True or false:  is an isosceles triangle.
is an isosceles triangle.
Given: Regular Pentagon 




True or false: 
Tap to reveal answer
Below is regular Pentagon  with center
with center  , a segment drawn from
, a segment drawn from  to each vertex - that is, each of its radii drawn.
to each vertex - that is, each of its radii drawn.

By symmetry, all of the radii of a regular pentagon are congruent - specifically,  . This triangle has at least two congruent sides, so it is isosceles.
. This triangle has at least two congruent sides, so it is isosceles.
Below is regular Pentagon 



By symmetry, all of the radii of a regular pentagon are congruent - specifically, 
← Didn't Know|Knew It →

Refer to the above triangle. By what statement does it follow that  ?
?

Refer to the above triangle. By what statement does it follow that 
Tap to reveal answer
We are given that, in  , two angles are congruent; specifically,
, two angles are congruent; specifically,  . It is a consequence of the Converse of the Isosceles Triangle Theorem that the sides opposite the angles are also congruent - that is, .
. It is a consequence of the Converse of the Isosceles Triangle Theorem that the sides opposite the angles are also congruent - that is, . .
.
We are given that, in 


← Didn't Know|Knew It →
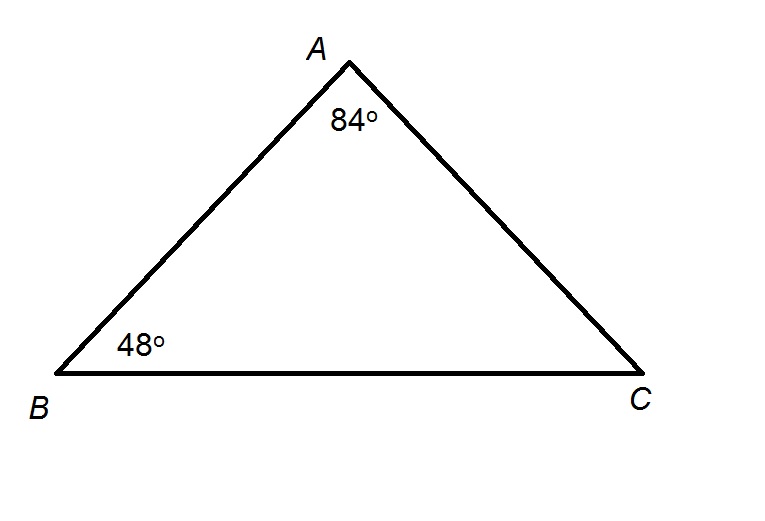
Figure NOT drawn to scale.
Refer to the above diagram.
True or false:  .
.

Figure NOT drawn to scale.
Refer to the above diagram.
True or false: 
Tap to reveal answer
The sum of the measures of the interior angles of a triangle is  , so
, so

Substitute the given two angle measures and solve for  :
:


Subtract 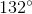 from both sides:
from both sides:


 , so, by the Converse of the Isosceles Triangle Theorem, their opposite sides are also congruent - that is,
, so, by the Converse of the Isosceles Triangle Theorem, their opposite sides are also congruent - that is,

The sum of the measures of the interior angles of a triangle is 
Substitute the given two angle measures and solve for 
Subtract 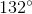

← Didn't Know|Knew It →
A triangle has a perimeter of  inches with one side of length
inches with one side of length  inches. If the remaining two sides have lengths in a ratio of
inches. If the remaining two sides have lengths in a ratio of  , what is length of the shortest side of the triangle?
, what is length of the shortest side of the triangle?
A triangle has a perimeter of 


Tap to reveal answer
The answer is  .
.
Since we know that the permieter is 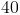 inches and one side is
inches and one side is  inches, it can be determined that the remaining two sides must combine to be
inches, it can be determined that the remaining two sides must combine to be  inches. The ratio of the remaining two sides is
inches. The ratio of the remaining two sides is 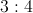 which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation
which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation  , and divide both sides by
, and divide both sides by  which means
which means  . The ratio of the remaining side lengths then becomes
. The ratio of the remaining side lengths then becomes  or
or  . We now know the 3 side lengths are
. We now know the 3 side lengths are 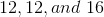 .
.
 is the shortest side and thus the answer.
is the shortest side and thus the answer.
The answer is 
Since we know that the permieter is 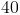


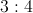





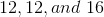

← Didn't Know|Knew It →
Given  such that
such that  ,
,  ,
,  , which of the following statements is true?
, which of the following statements is true?
Given 



Tap to reveal answer
Having three sides of different lengths, this triangle is scalene. In any scalene triangle, the angle with greatest measure is opposite the longest side, and the angle with least measure is opposite the shortest side. Therefore, since  , their opposite angles would be in order from greatest to least measure - that is,
, their opposite angles would be in order from greatest to least measure - that is,  .
.
Having three sides of different lengths, this triangle is scalene. In any scalene triangle, the angle with greatest measure is opposite the longest side, and the angle with least measure is opposite the shortest side. Therefore, since 

← Didn't Know|Knew It →
Find the perimeter of the triangle below.

Find the perimeter of the triangle below.

Tap to reveal answer
Use the Pythagorean Theorem to find the base of the right triangle.




Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.

Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.
← Didn't Know|Knew It →
Find the perimeter of the triangle below.

Find the perimeter of the triangle below.

Tap to reveal answer
Use the Pythagorean Theorem to find the base of the right triangle.




Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.

Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:

To find the perimeter, add up all the sides.
← Didn't Know|Knew It →
If a triangle has side lengths of  and
and  , which of the following can be a length of the third side?
, which of the following can be a length of the third side?
If a triangle has side lengths of 

Tap to reveal answer

The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:



The side length of  is the only choice that fits this criteria:
is the only choice that fits this criteria:




The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:
The side length of 
← Didn't Know|Knew It →
If a triangle has side lengths of  and
and  , which of the following could be the length of the third side?
, which of the following could be the length of the third side?
If a triangle has side lengths of 

Tap to reveal answer

The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:



The side length of  is the only choice that fits this criteria:
is the only choice that fits this criteria:




The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:
The side length of 
← Didn't Know|Knew It →
A triangle has sides of lengths 14, 18, and 20. Is the triangle scalene or isosceles?
A triangle has sides of lengths 14, 18, and 20. Is the triangle scalene or isosceles?
Tap to reveal answer
A triangle with three sides of different length is, by definition, scalene.
A triangle with three sides of different length is, by definition, scalene.
← Didn't Know|Knew It →
Given: Regular Pentagon  with center
with center  . Construct segments
. Construct segments  and
and  to form
to form  .
.
True or false:  is an isosceles triangle.
is an isosceles triangle.
Given: Regular Pentagon 




True or false: 
Tap to reveal answer
Below is regular Pentagon  with center
with center  , a segment drawn from
, a segment drawn from  to each vertex - that is, each of its radii drawn.
to each vertex - that is, each of its radii drawn.

By symmetry, all of the radii of a regular pentagon are congruent - specifically,  . This triangle has at least two congruent sides, so it is isosceles.
. This triangle has at least two congruent sides, so it is isosceles.
Below is regular Pentagon 



By symmetry, all of the radii of a regular pentagon are congruent - specifically, 
← Didn't Know|Knew It →

Refer to the above triangle. By what statement does it follow that  ?
?

Refer to the above triangle. By what statement does it follow that 
Tap to reveal answer
We are given that, in  , two angles are congruent; specifically,
, two angles are congruent; specifically,  . It is a consequence of the Converse of the Isosceles Triangle Theorem that the sides opposite the angles are also congruent - that is, .
. It is a consequence of the Converse of the Isosceles Triangle Theorem that the sides opposite the angles are also congruent - that is, . .
.
We are given that, in 


← Didn't Know|Knew It →

Figure NOT drawn to scale.
Refer to the above diagram.
True or false:  .
.

Figure NOT drawn to scale.
Refer to the above diagram.
True or false: 
Tap to reveal answer
The sum of the measures of the interior angles of a triangle is  , so
, so

Substitute the given two angle measures and solve for  :
:


Subtract 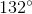 from both sides:
from both sides:


 , so, by the Converse of the Isosceles Triangle Theorem, their opposite sides are also congruent - that is,
, so, by the Converse of the Isosceles Triangle Theorem, their opposite sides are also congruent - that is,

The sum of the measures of the interior angles of a triangle is 
Substitute the given two angle measures and solve for 
Subtract 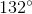

← Didn't Know|Knew It →