How to find the volume of a cone - Math
Card 1 of 60
You have an empty cylinder with a base diameter of 6 and a height of 10 and you have a cone full of water with a base radius of 3 and a height of 10. If you empty the cone of water into the cylinder, how much volume is left empty in the cylinder?
You have an empty cylinder with a base diameter of 6 and a height of 10 and you have a cone full of water with a base radius of 3 and a height of 10. If you empty the cone of water into the cylinder, how much volume is left empty in the cylinder?
Tap to reveal answer
Cylinder Volume = 
Cone Volume = 
Cylinder Diameter = 6, therefore Cylinder Radius = 3
Cone Radius = 3
Empty Volume = Cylinder Volume – Cone Volume




Cylinder Volume =
Cone Volume =
Cylinder Diameter = 6, therefore Cylinder Radius = 3
Cone Radius = 3
Empty Volume = Cylinder Volume – Cone Volume
← Didn't Know|Knew It →
What is the volume of a right cone with a diameter of 6 cm and a height of 5 cm?
What is the volume of a right cone with a diameter of 6 cm and a height of 5 cm?
Tap to reveal answer
The general formula is given by V = 1/3Bh = 1/3pi $r^{2}$h, where  = radius and
= radius and  = height.
= height.
The diameter is 6 cm, so the radius is 3 cm.

The general formula is given by V = 1/3Bh = 1/3pi $r^{2}$h, where 

The diameter is 6 cm, so the radius is 3 cm.
← Didn't Know|Knew It →
There is a large cone with a radius of 4 meters and height of 18 meters. You can fill the cone with water at a rate of 3 cubic meters every 25 seconds. How long will it take you to fill the cone?
There is a large cone with a radius of 4 meters and height of 18 meters. You can fill the cone with water at a rate of 3 cubic meters every 25 seconds. How long will it take you to fill the cone?
Tap to reveal answer
First we will calculate the volume of the cone

Next we will determine the time it will take to fill that volume

We will then convert that into minutes

First we will calculate the volume of the cone
Next we will determine the time it will take to fill that volume
We will then convert that into minutes
← Didn't Know|Knew It →
What is the volume of a cone with a height of  and a base with a radius of
and a base with a radius of  ?
?
What is the volume of a cone with a height of 

Tap to reveal answer
To find the volume of a cone we must use the equation  . In this formula,
. In this formula,  is the area of the circular base of the cone, and
is the area of the circular base of the cone, and  is the height of the cone.
is the height of the cone.
We must first solve for the area of the base using  .
.
The equation for the area of a circle is  . Using this, we can adjust our formula and plug in the value of our radius.
. Using this, we can adjust our formula and plug in the value of our radius.



Now we can plug in our given height,  .
.

Multiply everything out to solve for the volume.

The volume of the cone is  .
.
To find the volume of a cone we must use the equation 


We must first solve for the area of the base using 
The equation for the area of a circle is 
Now we can plug in our given height, 
Multiply everything out to solve for the volume.
The volume of the cone is 
← Didn't Know|Knew It →
What is the equation of a circle with a center of (5,15) and a radius of 7?
What is the equation of a circle with a center of (5,15) and a radius of 7?
Tap to reveal answer
To find the equation of a circle we must first know the standard form of the equation of a circle which is 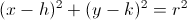
The letters  and
and  represent the
represent the  -value and
-value and  -value of the center of the circle respectively.
-value of the center of the circle respectively.
In this case  is 5 and k is 15 so plugging the values into the equation yields
is 5 and k is 15 so plugging the values into the equation yields 
We then plug the radius into the equation to get 
Square it to yield 
The equation with a center of (5,15) and a radius of 7 is  .
.
To find the equation of a circle we must first know the standard form of the equation of a circle which is
The letters 



In this case 
We then plug the radius into the equation to get
Square it to yield
The equation with a center of (5,15) and a radius of 7 is 
← Didn't Know|Knew It →
What is the volume of a cone with base radius 4, and height 6?
What is the volume of a cone with base radius 4, and height 6?
Tap to reveal answer
The volume of a cone is  , where
, where  is the height of the cone and
is the height of the cone and  is the base radius.
is the base radius.
The volume of this cone is thus:

= 
The volume of a cone is 


The volume of this cone is thus:
=
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
What is the volume of a cone that has a radius of 3 and a height of 4?
What is the volume of a cone that has a radius of 3 and a height of 4?
Tap to reveal answer
The standard equation for the volume of a cone is

where  denotes the radius and
denotes the radius and  denotes the height.
denotes the height.
Plug in the given values for  and
and  to find the answer:
to find the answer:

The standard equation for the volume of a cone is
where 

Plug in the given values for 

← Didn't Know|Knew It →
Find the volume of the following cone.

Find the volume of the following cone.

Tap to reveal answer
The formula for the volume of a cone is:

where  is the radius of the cone and
is the radius of the cone and  is the height of the cone.
is the height of the cone.
In order to find the height of the cone, use the Pythagorean Theorem:




Plugging in our values, we get:


The formula for the volume of a cone is:
where 

In order to find the height of the cone, use the Pythagorean Theorem:
Plugging in our values, we get:
← Didn't Know|Knew It →
Find the volume of the following cone.

Find the volume of the following cone.

Tap to reveal answer
The formula for the volume of a cone is:

Where  is the radius of the cone and
is the radius of the cone and  is the height of the cone
is the height of the cone
Use the Pythagorean Theorem to find the length of the radius:



Plugging in our values, we get:


The formula for the volume of a cone is:
Where 

Use the Pythagorean Theorem to find the length of the radius:
Plugging in our values, we get:
← Didn't Know|Knew It →
Find the volume of the following half cone.

Find the volume of the following half cone.

Tap to reveal answer
The formula of the volume of a half cone is:


Where  is the radius of the cone and
is the radius of the cone and  is the height of the cone.
is the height of the cone.
Use the Pythagorean Theorem to find the height of the cone:





The formula of the volume of a half cone is:
Where 

Use the Pythagorean Theorem to find the height of the cone:
← Didn't Know|Knew It →
You have an empty cylinder with a base diameter of 6 and a height of 10 and you have a cone full of water with a base radius of 3 and a height of 10. If you empty the cone of water into the cylinder, how much volume is left empty in the cylinder?
You have an empty cylinder with a base diameter of 6 and a height of 10 and you have a cone full of water with a base radius of 3 and a height of 10. If you empty the cone of water into the cylinder, how much volume is left empty in the cylinder?
Tap to reveal answer
Cylinder Volume = 
Cone Volume = 
Cylinder Diameter = 6, therefore Cylinder Radius = 3
Cone Radius = 3
Empty Volume = Cylinder Volume – Cone Volume




Cylinder Volume =
Cone Volume =
Cylinder Diameter = 6, therefore Cylinder Radius = 3
Cone Radius = 3
Empty Volume = Cylinder Volume – Cone Volume
← Didn't Know|Knew It →
What is the volume of a right cone with a diameter of 6 cm and a height of 5 cm?
What is the volume of a right cone with a diameter of 6 cm and a height of 5 cm?
Tap to reveal answer
The general formula is given by V = 1/3Bh = 1/3pi $r^{2}$h, where  = radius and
= radius and  = height.
= height.
The diameter is 6 cm, so the radius is 3 cm.

The general formula is given by V = 1/3Bh = 1/3pi $r^{2}$h, where 

The diameter is 6 cm, so the radius is 3 cm.
← Didn't Know|Knew It →
There is a large cone with a radius of 4 meters and height of 18 meters. You can fill the cone with water at a rate of 3 cubic meters every 25 seconds. How long will it take you to fill the cone?
There is a large cone with a radius of 4 meters and height of 18 meters. You can fill the cone with water at a rate of 3 cubic meters every 25 seconds. How long will it take you to fill the cone?
Tap to reveal answer
First we will calculate the volume of the cone

Next we will determine the time it will take to fill that volume

We will then convert that into minutes

First we will calculate the volume of the cone
Next we will determine the time it will take to fill that volume
We will then convert that into minutes
← Didn't Know|Knew It →
What is the volume of a cone with a height of  and a base with a radius of
and a base with a radius of  ?
?
What is the volume of a cone with a height of 

Tap to reveal answer
To find the volume of a cone we must use the equation  . In this formula,
. In this formula,  is the area of the circular base of the cone, and
is the area of the circular base of the cone, and  is the height of the cone.
is the height of the cone.
We must first solve for the area of the base using  .
.
The equation for the area of a circle is  . Using this, we can adjust our formula and plug in the value of our radius.
. Using this, we can adjust our formula and plug in the value of our radius.



Now we can plug in our given height,  .
.

Multiply everything out to solve for the volume.

The volume of the cone is  .
.
To find the volume of a cone we must use the equation 


We must first solve for the area of the base using 
The equation for the area of a circle is 
Now we can plug in our given height, 
Multiply everything out to solve for the volume.
The volume of the cone is 
← Didn't Know|Knew It →
What is the equation of a circle with a center of (5,15) and a radius of 7?
What is the equation of a circle with a center of (5,15) and a radius of 7?
Tap to reveal answer
To find the equation of a circle we must first know the standard form of the equation of a circle which is 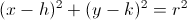
The letters  and
and  represent the
represent the  -value and
-value and  -value of the center of the circle respectively.
-value of the center of the circle respectively.
In this case  is 5 and k is 15 so plugging the values into the equation yields
is 5 and k is 15 so plugging the values into the equation yields 
We then plug the radius into the equation to get 
Square it to yield 
The equation with a center of (5,15) and a radius of 7 is  .
.
To find the equation of a circle we must first know the standard form of the equation of a circle which is
The letters 



In this case 
We then plug the radius into the equation to get
Square it to yield
The equation with a center of (5,15) and a radius of 7 is 
← Didn't Know|Knew It →
What is the volume of a cone with base radius 4, and height 6?
What is the volume of a cone with base radius 4, and height 6?
Tap to reveal answer
The volume of a cone is  , where
, where  is the height of the cone and
is the height of the cone and  is the base radius.
is the base radius.
The volume of this cone is thus:

= 
The volume of a cone is 


The volume of this cone is thus:
=
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
What is the volume of a cone that has a radius of 3 and a height of 4?
What is the volume of a cone that has a radius of 3 and a height of 4?
Tap to reveal answer
The standard equation for the volume of a cone is

where  denotes the radius and
denotes the radius and  denotes the height.
denotes the height.
Plug in the given values for  and
and  to find the answer:
to find the answer:

The standard equation for the volume of a cone is
where 

Plug in the given values for 

← Didn't Know|Knew It →
Find the volume of the following cone.

Find the volume of the following cone.

Tap to reveal answer
The formula for the volume of a cone is:

where  is the radius of the cone and
is the radius of the cone and  is the height of the cone.
is the height of the cone.
In order to find the height of the cone, use the Pythagorean Theorem:




Plugging in our values, we get:


The formula for the volume of a cone is:
where 

In order to find the height of the cone, use the Pythagorean Theorem:
Plugging in our values, we get:
← Didn't Know|Knew It →



