Acute / Obtuse Isosceles Triangles - Math
Card 1 of 224
An isosceles triangle has a base of 12 cm and an area of 42 $cm^{2}$. What must be the height of this triangle?
An isosceles triangle has a base of 12 cm and an area of 42 $cm^{2}$. What must be the height of this triangle?
Tap to reveal answer
A=\frac{1}{2}$bh.
6x=42
x=7
A=\frac{1}{2}$bh.
6x=42
x=7
← Didn't Know|Knew It →
One side of an acute isosceles triangle is 15 feet. Another side is 5 feet. What is the perimeter of the triangle in feet?
One side of an acute isosceles triangle is 15 feet. Another side is 5 feet. What is the perimeter of the triangle in feet?
Tap to reveal answer
Because this is an acute isosceles triangle, the third side must be the same as the longer of the sides that you were given. To find the perimeter, multiply the longer side by 2 and add the shorter side.
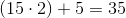
Because this is an acute isosceles triangle, the third side must be the same as the longer of the sides that you were given. To find the perimeter, multiply the longer side by 2 and add the shorter side.
← Didn't Know|Knew It →
An isosceles triangle has a base of 12 cm and an area of 42 $cm^{2}$. What must be the height of this triangle?
An isosceles triangle has a base of 12 cm and an area of 42 $cm^{2}$. What must be the height of this triangle?
Tap to reveal answer
A=\frac{1}{2}$bh.
6x=42
x=7
A=\frac{1}{2}$bh.
6x=42
x=7
← Didn't Know|Knew It →
An isosceles triangle has a perimeter of 
. If the base of the triangle is two less than two times the length of each leg, what is the height of the triangle?
An isosceles triangle has a perimeter of
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
An isosceles triangle has a perimeter of 
. If the base of the triangle is 
less than three times the length of a leg, what is the height of the triangle?
An isosceles triangle has a perimeter of
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
An isosceles triangle has a perimeter of 
. If the length of the base is one less than twice the length of a leg, what is the height of the triangle?
An isosceles triangle has a perimeter of
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
An isosceles triangle has a perimeter of 
. If the length of the base is fourteen less than three times the length of a leg, what is the height of the triangle?
An isosceles triangle has a perimeter of
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
An isosceles triangle has a perimeter of 
. If the length of the base is seven more than one-seventh of the length of a leg, what is the height of the triangle?
An isosceles triangle has a perimeter of
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
An isosceles triangle has a perimeter of 
. If the length of the base is two less than one-third of the length of a leg, what is the height of the triangle?
An isosceles triangle has a perimeter of
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
An isosceles triangle has a perimeter of 
. If the length of the base is ten less than twice the length of a leg, what is the height of the triangle?
An isosceles triangle has a perimeter of
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
An isosceles triangle has a perimeter of 
. If the length of the base is four more than one-third of the length of a leg, what is the height of the triangle?
An isosceles triangle has a perimeter of
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
The perimeter of an isosceles triangle is 
. If the length of the base is five more than one-fourth the length of a leg, what is the height of the triangle?
The perimeter of an isosceles triangle is
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
The perimeter of an isosceles triangle is 
. If the length of the base is ten more than one-eighth the length of a leg, what is the height of the triangle?
The perimeter of an isosceles triangle is
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
The perimeter of an isosceles triangle is 
. If the length of the base is eleven less than twice the length of a leg, what is the height of the triangle?
The perimeter of an isosceles triangle is
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
The perimeter of an isosceles triangle is 
. If the length of the base is fifteen more than one-third the length of a leg, what is the height of the triangle?
The perimeter of an isosceles triangle is
Tap to reveal answer
First, find the lengths of the triangle.
Let 
be the length of each leg. Then, the length of the base must be 
.
Use the information given about the perimeter to solve for 
.
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
places after the decimal.
First, find the lengths of the triangle.
Let
Use the information given about the perimeter to solve for
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.
Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to
← Didn't Know|Knew It →
A triangle has a perimeter of 
inches with one side of length 
inches. If the remaining two sides have lengths in a ratio of 
, what is length of the shortest side of the triangle?
A triangle has a perimeter of
Tap to reveal answer
The answer is 
.
Since we know that the permieter is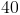 
inches and one side is 
inches, it can be determined that the remaining two sides must combine to be 
inches. The ratio of the remaining two sides is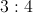 
which means 3 parts : 4 parts or 7 parts combined. We can then set up the equation 
, and divide both sides by 
which means 
. The ratio of the remaining side lengths then becomes 
or 
. We now know the 3 side lengths are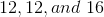 
.
is the shortest side and thus the answer.
The answer is
Since we know that the permieter is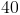
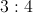
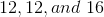
← Didn't Know|Knew It →
An isosceles triangle has a base of 12 cm and an area of 42 $cm^{2}$. What must be the height of this triangle?
An isosceles triangle has a base of 12 cm and an area of 42 $cm^{2}$. What must be the height of this triangle?
Tap to reveal answer
A=\frac{1}{2}$bh.
6x=42
x=7
A=\frac{1}{2}$bh.
6x=42
x=7
← Didn't Know|Knew It →
Given 
such that 
, 
, 
, which of the following statements is true?
Given
Tap to reveal answer
Having three sides of different lengths, this triangle is scalene. In any scalene triangle, the angle with greatest measure is opposite the longest side, and the angle with least measure is opposite the shortest side. Therefore, since 
, their opposite angles would be in order from greatest to least measure - that is, 
.
Having three sides of different lengths, this triangle is scalene. In any scalene triangle, the angle with greatest measure is opposite the longest side, and the angle with least measure is opposite the shortest side. Therefore, since
← Didn't Know|Knew It →
Find the perimeter of the triangle below.
Find the perimeter of the triangle below.
Tap to reveal answer
Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:
To find the perimeter, add up all the sides.
Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:
To find the perimeter, add up all the sides.
← Didn't Know|Knew It →
Find the perimeter of the triangle below.
Find the perimeter of the triangle below.
Tap to reveal answer
Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:
To find the perimeter, add up all the sides.
Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:
To find the perimeter, add up all the sides.
← Didn't Know|Knew It →