Functions and Graphs - Math
Card 1 of 504
Factor the polynomial if the expression is equal to zero when  .
.

Factor the polynomial if the expression is equal to zero when 
Tap to reveal answer
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression  fits the description of the zeroes.
fits the description of the zeroes.
Now we need to check the answer.


We are able to get back to the original expression, meaning that the answer is  .
.
Knowing the zeroes makes it relatively easy to factor the polynomial.
The expression 
Now we need to check the answer.
We are able to get back to the original expression, meaning that the answer is 
← Didn't Know|Knew It →
A polyomial with leading term  has 5 and 7 as roots; 7 is a double root. What is this polynomial?
has 5 and 7 as roots; 7 is a double root. What is this polynomial?
A polyomial with leading term 
Tap to reveal answer
Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is  . To put this in expanded form:
. To put this in expanded form:






Since 5 is a single root and 7 is a double root, and the degree of the polynomial is 3, the polynomial is 
← Didn't Know|Knew It →
A polyomial with leading term  has 6 as a triple root. What is this polynomial?
has 6 as a triple root. What is this polynomial?
A polyomial with leading term 
Tap to reveal answer
Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is  , which we can expland using the cube of a binomial pattern.
, which we can expland using the cube of a binomial pattern.


Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is 
← Didn't Know|Knew It →
What are the solutions to  ?
?
What are the solutions to 
Tap to reveal answer
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of  such that the output will be zero. Thus, we first factor the equation.
such that the output will be zero. Thus, we first factor the equation.

Then, we are looking for the values where each of these factors are equal to zero.
 implies
implies 
and  implies
implies 
Thus, these are our solutions.
When we are looking for the solutions of a quadratic, or the zeroes, we are looking for the values of 
Then, we are looking for the values where each of these factors are equal to zero.

and 
Thus, these are our solutions.
← Didn't Know|Knew It →
Simplify the following polynomial function:

Simplify the following polynomial function:
Tap to reveal answer
First, multiply the outside term with each term within the parentheses:


Rearranging the polynomial into fractional form, we get:

First, multiply the outside term with each term within the parentheses:
Rearranging the polynomial into fractional form, we get:
← Didn't Know|Knew It →
Simplify the following polynomial:

Simplify the following polynomial:
Tap to reveal answer
To simplify the polynomial, begin by combining like terms:


To simplify the polynomial, begin by combining like terms:
← Didn't Know|Knew It →
What is the minimal value of

over all real numbers?
What is the minimal value of
over all real numbers?
Tap to reveal answer
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The  -coordinate for the vertex of any parabola of the form
-coordinate for the vertex of any parabola of the form

is at
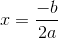
So here,



We plug this value back into the equation of the parabola, to find the value of the function at this 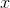 .
.

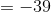
Thus the minimal value of the expression is  .
.
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The 
is at
So here,
We plug this value back into the equation of the parabola, to find the value of the function at this 
Thus the minimal value of the expression is 
← Didn't Know|Knew It →
A conic section is represented by the following equation:

What type of conic section does this equation represent?
A conic section is represented by the following equation:
What type of conic section does this equation represent?
Tap to reveal answer
The simplest way to know what kind of conic section an equation represents is by checking the coefficients in front of each variable. The equation must be in general form while you do this check. Luckily, this equation is already in general form, so it's easy to see. The general equation for a conic section is the following:

Assuming the term  is 0 (which it usually is):
is 0 (which it usually is):
- If A equals C, the equation is a circle.
- If A and C have the same sign (but are not equal to each other), the equation is an ellipse.
- If either A or C equals 0, the equation is a parabola.
- If A and C are different signs (i.e. one is negative and one is positive), the equation is a hyperbola.
The simplest way to know what kind of conic section an equation represents is by checking the coefficients in front of each variable. The equation must be in general form while you do this check. Luckily, this equation is already in general form, so it's easy to see. The general equation for a conic section is the following:
Assuming the term 
- If A equals C, the equation is a circle.
- If A and C have the same sign (but are not equal to each other), the equation is an ellipse.
- If either A or C equals 0, the equation is a parabola.
- If A and C are different signs (i.e. one is negative and one is positive), the equation is a hyperbola.
← Didn't Know|Knew It →
Solve for  :
: 
Solve for 
Tap to reveal answer




FOIL: 






These are our possible solutions. However, we need to test them.
 :
:






The equation becomes  . This is true, so
. This is true, so  is a solution.
is a solution.
 :
:



However, negative numbers do not have logarithms, so this equation is meaningless.  is not a solution, and
is not a solution, and  is the one and only solution. Since this is not one of our choices, the correct response is "The correct solution set is not included among the other choices."
is the one and only solution. Since this is not one of our choices, the correct response is "The correct solution set is not included among the other choices."
FOIL:
These are our possible solutions. However, we need to test them.

The equation becomes 


However, negative numbers do not have logarithms, so this equation is meaningless. 

← Didn't Know|Knew It →
Find the vertex  for a parabola with equation
for a parabola with equation
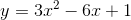
Find the vertex 
Tap to reveal answer
For any parabola of the form 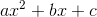 , the
, the 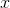 -coordinate of its vertex is
-coordinate of its vertex is
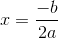
So here, we have

= 
We plug this back into the original equation to find 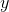 :
:

= 
For any parabola of the form 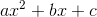
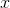
So here, we have
=
We plug this back into the original equation to find 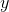
=
← Didn't Know|Knew It →
What is the center and radius of the circle indicated by the equation?

What is the center and radius of the circle indicated by the equation?
Tap to reveal answer
A circle is defined by an equation in the format  .
.
The center is indicated by the point  and the radius
and the radius  .
.
In the equation  , the center is
, the center is  and the radius is
and the radius is  .
.
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 


← Didn't Know|Knew It →
What is the domain of the function below?

What is the domain of the function below?
Tap to reveal answer
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:

The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:

Therefore, the domain is  .
.
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:
The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:
Therefore, the domain is 
← Didn't Know|Knew It →
What is the domain of the function below:

What is the domain of the function below:
Tap to reveal answer
The domain is defined as the set of possible values for the x variable. In order to find the impossible values of x, we should:
a) Set the equation under the radical equal to zero and look for probable x values that make the expression inside the radical negative:


There is no real value for x that will fit this equation, because any real value square is a positive number i.e. cannot be a negative number.
b) Set the denominator of the fractional function equal to zero and look for probable x values:

Now we can solve the equation for x:

There is no real value for x that will fit this equation.
The radical is always positive and denominator is never equal to zero, so the f(x) is defined for all real values of x. That means the set of all real numbers is the domain of the f(x) and the correct answer is  .
.
Alternative solution for the second part of the solution:
After figuring out that the expression under the radical is always positive (part a), we can solve the radical and therefore denominator for the least possible value (minimum value). Setting the x value equal to zero will give the minimum possible value for the denominator.


![\sqrt[4]{0+1}-$\frac{1}{2}$=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138727/gif.latex)

That means the denominator will always be a positive value greater than 1/2; thus it cannot be equal to zero by setting any real value for x. Therefore the set of all real numbers is the domain of the f(x).
The domain is defined as the set of possible values for the x variable. In order to find the impossible values of x, we should:
a) Set the equation under the radical equal to zero and look for probable x values that make the expression inside the radical negative:
There is no real value for x that will fit this equation, because any real value square is a positive number i.e. cannot be a negative number.
b) Set the denominator of the fractional function equal to zero and look for probable x values:
Now we can solve the equation for x:
There is no real value for x that will fit this equation.
The radical is always positive and denominator is never equal to zero, so the f(x) is defined for all real values of x. That means the set of all real numbers is the domain of the f(x) and the correct answer is 
Alternative solution for the second part of the solution:
After figuring out that the expression under the radical is always positive (part a), we can solve the radical and therefore denominator for the least possible value (minimum value). Setting the x value equal to zero will give the minimum possible value for the denominator.
That means the denominator will always be a positive value greater than 1/2; thus it cannot be equal to zero by setting any real value for x. Therefore the set of all real numbers is the domain of the f(x).
← Didn't Know|Knew It →
What is the domain of the function below:

What is the domain of the function below:
Tap to reveal answer
The domain is defined as the set of all possible values of the independent variable  . First,
. First,  must be greater than or equal to zero, because if
must be greater than or equal to zero, because if  , then
, then will be undefined. In addition, the total expression under the radical, i.e.
will be undefined. In addition, the total expression under the radical, i.e.  must be greater than or equal to zero:
must be greater than or equal to zero:




That means that the expression under the radical is always positive and therefore  is defined. Hence, the domain of the function
is defined. Hence, the domain of the function  is
is  .
.
The domain is defined as the set of all possible values of the independent variable 




That means that the expression under the radical is always positive and therefore 


← Didn't Know|Knew It →
You are given that  and
and  .
.
Which of the following is equal to  ?
?
You are given that 

Which of the following is equal to 
Tap to reveal answer
Since  and
and  , it follows that
, it follows that  and
and 

Since 


← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
What is  ?
?
What is 
Tap to reveal answer
Recall that by definition a logarithm is the inverse of the exponential function. Thus, our logarithm corresponds to the value of  in the equation:
in the equation:
 .
.
We know that  and thus our answer is
and thus our answer is  .
.
Recall that by definition a logarithm is the inverse of the exponential function. Thus, our logarithm corresponds to the value of 

We know that 

← Didn't Know|Knew It →
A conic section is represented by the following equation:

Which of the following best describes this equation?
A conic section is represented by the following equation:
Which of the following best describes this equation?
Tap to reveal answer
First, we need to make sure the conic section equation is in a form we recognize. Luckily, this equation is already in standard form:

The first step is to determine the type of conic section this equation represents. Because there are two squared variables ( and
and  ), this equation cannot be a parabola. Because the coefficients in front of the squared variables are different signs (i.e. one is negative and the other is positive), this equation must be a hyperbola, not an ellipse.
), this equation cannot be a parabola. Because the coefficients in front of the squared variables are different signs (i.e. one is negative and the other is positive), this equation must be a hyperbola, not an ellipse.
In a hyperbola, the squared term with a positive coefficient represents the direction in which the hyperbola opens. In other words, if the  term is positive, the hyperbola opens horizontally. If the
term is positive, the hyperbola opens horizontally. If the  term is positive, the hyperbola opens vertically. Therefore, this is a horizontal hyperbola.
term is positive, the hyperbola opens vertically. Therefore, this is a horizontal hyperbola.
The center is always found at  , which in this case is
, which in this case is  .
.
That leaves only the asymptotes. For a hyperbola, the slopes of the asymptotes can be found by dividing  by
by  (remember to always put the vertical value,
(remember to always put the vertical value,  , above the horizontal value,
, above the horizontal value,  ). Remember that these slopes always come in pairs, with one being positive and the other being negative.
). Remember that these slopes always come in pairs, with one being positive and the other being negative.
In this case,  is 3 and
is 3 and  is 2, so we get slopes of
is 2, so we get slopes of  and
and  .
.
First, we need to make sure the conic section equation is in a form we recognize. Luckily, this equation is already in standard form:
The first step is to determine the type of conic section this equation represents. Because there are two squared variables (

In a hyperbola, the squared term with a positive coefficient represents the direction in which the hyperbola opens. In other words, if the 

The center is always found at 

That leaves only the asymptotes. For a hyperbola, the slopes of the asymptotes can be found by dividing 



In this case, 



← Didn't Know|Knew It →
What is the center and radius of the circle indicated by the equation?

What is the center and radius of the circle indicated by the equation?
Tap to reveal answer
A circle is defined by an equation in the format  .
.
The center is indicated by the point  and the radius
and the radius  .
.
In the equation  , the center is
, the center is  and the radius is
and the radius is  .
.
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 


← Didn't Know|Knew It →
What is the shape of the graph indicated by the equation?

What is the shape of the graph indicated by the equation?
Tap to reveal answer
An ellipse has an equation that can be written in the format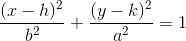 . The center is indicated by
. The center is indicated by 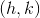 , or in this case
, or in this case  .
.
An ellipse has an equation that can be written in the format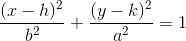

← Didn't Know|Knew It →


