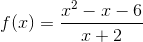Limits - Math
Card 1 of 24
Tap to reveal answer
A limit describes what  -value a function approaches as
-value a function approaches as  approaches a certain value (in this case,
approaches a certain value (in this case, 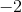 ). The easiest way to find what
). The easiest way to find what  -value a function approaches is to substitute the
-value a function approaches is to substitute the  -value into the equation.
-value into the equation.

Substituting  for
for  gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
One method of finding the limit is to try and simplify the equation as much as possible:

As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:

Even though the domain of the original function is restricted ( cannot equal
cannot equal  ), we can still substitute into this simplified equation to find the limit at
), we can still substitute into this simplified equation to find the limit at 

A limit describes what 

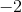


Substituting 

One method of finding the limit is to try and simplify the equation as much as possible:
As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:
Even though the domain of the original function is restricted (

← Didn't Know|Knew It →
Evaluate the limit below:

Evaluate the limit below:
Tap to reveal answer
 will approach
will approach  when
when  approaches
approaches  , so
, so 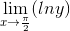 will be of type
will be of type  as shown below:
as shown below:

So, we can apply the L’ Hospital's Rule:


since:

hence:





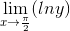

So, we can apply the L’ Hospital's Rule:
since:
hence:
← Didn't Know|Knew It →
The speed of a car traveling on the highway is given by the following function of time:

What can you say about the car's speed after a long time (that is, as  approaches infinity)?
approaches infinity)?
The speed of a car traveling on the highway is given by the following function of time:
What can you say about the car's speed after a long time (that is, as 
Tap to reveal answer
The function given is a polynomial with a term  , such that
, such that  is greater than 1.
is greater than 1.
Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as  approaches infinity.
approaches infinity.
This tells us that the given function is not a very realistic description of a car's speed for large  !
!
The function given is a polynomial with a term 

Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as 
This tells us that the given function is not a very realistic description of a car's speed for large 
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Calculate  .
.
Calculate 
Tap to reveal answer
This can be rewritten as follows:


![= $\lim_{x\rightarrow \infty }$\left [\left ( $x^{2}$-1 \right ) \cdot \sin $\frac{1}{ $x^{2}$$-1} \right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99922/gif.latex)

We can substitute  , noting that as
, noting that as  ,
,  :
:
 , which is the correct choice.
, which is the correct choice.
This can be rewritten as follows:
We can substitute 



← Didn't Know|Knew It →
Evaluate the limit below:

Evaluate the limit below:
Tap to reveal answer
 will approach
will approach  when
when  approaches
approaches  , so
, so 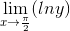 will be of type
will be of type  as shown below:
as shown below:

So, we can apply the L’ Hospital's Rule:


since:

hence:





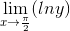

So, we can apply the L’ Hospital's Rule:
since:
hence:
← Didn't Know|Knew It →
Let  .
.
Find  .
.
Let 
Find 
Tap to reveal answer

This is a graph of  . We know that
. We know that  is undefined; therefore, there is no value for
is undefined; therefore, there is no value for  . But as we take a look at the graph, we can see that as
. But as we take a look at the graph, we can see that as  approaches 0 from the left,
approaches 0 from the left,  approaches negative infinity.
approaches negative infinity.
This can be illustrated by thinking of small negative numbers.


NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.
 is actually infinity, not negative infinity.
is actually infinity, not negative infinity.

This is a graph of 




This can be illustrated by thinking of small negative numbers.
NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.

← Didn't Know|Knew It →
Tap to reveal answer
A limit describes what  -value a function approaches as
-value a function approaches as  approaches a certain value (in this case,
approaches a certain value (in this case, 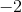 ). The easiest way to find what
). The easiest way to find what  -value a function approaches is to substitute the
-value a function approaches is to substitute the  -value into the equation.
-value into the equation.

Substituting  for
for  gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
One method of finding the limit is to try and simplify the equation as much as possible:

As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:

Even though the domain of the original function is restricted ( cannot equal
cannot equal  ), we can still substitute into this simplified equation to find the limit at
), we can still substitute into this simplified equation to find the limit at 

A limit describes what 

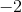


Substituting 

One method of finding the limit is to try and simplify the equation as much as possible:
As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:
Even though the domain of the original function is restricted (

← Didn't Know|Knew It →
Evaluate the limit below:

Evaluate the limit below:
Tap to reveal answer
 will approach
will approach  when
when  approaches
approaches  , so
, so 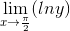 will be of type
will be of type  as shown below:
as shown below:

So, we can apply the L’ Hospital's Rule:


since:

hence:





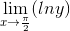

So, we can apply the L’ Hospital's Rule:
since:
hence:
← Didn't Know|Knew It →
Evaluate the limit below:

Evaluate the limit below:
Tap to reveal answer
 will approach
will approach  when
when  approaches
approaches  , so
, so 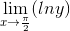 will be of type
will be of type  as shown below:
as shown below:

So, we can apply the L’ Hospital's Rule:


since:

hence:





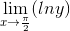

So, we can apply the L’ Hospital's Rule:
since:
hence:
← Didn't Know|Knew It →
The speed of a car traveling on the highway is given by the following function of time:

What can you say about the car's speed after a long time (that is, as  approaches infinity)?
approaches infinity)?
The speed of a car traveling on the highway is given by the following function of time:
What can you say about the car's speed after a long time (that is, as 
Tap to reveal answer
The function given is a polynomial with a term  , such that
, such that  is greater than 1.
is greater than 1.
Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as  approaches infinity.
approaches infinity.
This tells us that the given function is not a very realistic description of a car's speed for large  !
!
The function given is a polynomial with a term 

Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as 
This tells us that the given function is not a very realistic description of a car's speed for large 
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Calculate  .
.
Calculate 
Tap to reveal answer
This can be rewritten as follows:


![= $\lim_{x\rightarrow \infty }$\left [\left ( $x^{2}$-1 \right ) \cdot \sin $\frac{1}{ $x^{2}$$-1} \right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99922/gif.latex)

We can substitute  , noting that as
, noting that as  ,
,  :
:
 , which is the correct choice.
, which is the correct choice.
This can be rewritten as follows:
We can substitute 



← Didn't Know|Knew It →
Tap to reveal answer
A limit describes what  -value a function approaches as
-value a function approaches as  approaches a certain value (in this case,
approaches a certain value (in this case, 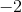 ). The easiest way to find what
). The easiest way to find what  -value a function approaches is to substitute the
-value a function approaches is to substitute the  -value into the equation.
-value into the equation.

Substituting  for
for  gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
One method of finding the limit is to try and simplify the equation as much as possible:

As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:

Even though the domain of the original function is restricted ( cannot equal
cannot equal  ), we can still substitute into this simplified equation to find the limit at
), we can still substitute into this simplified equation to find the limit at 

A limit describes what 

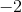


Substituting 

One method of finding the limit is to try and simplify the equation as much as possible:
As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:
Even though the domain of the original function is restricted (

← Didn't Know|Knew It →
Tap to reveal answer
A limit describes what  -value a function approaches as
-value a function approaches as  approaches a certain value (in this case,
approaches a certain value (in this case, 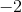 ). The easiest way to find what
). The easiest way to find what  -value a function approaches is to substitute the
-value a function approaches is to substitute the  -value into the equation.
-value into the equation.

Substituting  for
for  gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
One method of finding the limit is to try and simplify the equation as much as possible:

As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:

Even though the domain of the original function is restricted ( cannot equal
cannot equal  ), we can still substitute into this simplified equation to find the limit at
), we can still substitute into this simplified equation to find the limit at 

A limit describes what 

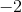


Substituting 

One method of finding the limit is to try and simplify the equation as much as possible:
As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:
Even though the domain of the original function is restricted (

← Didn't Know|Knew It →
Let  .
.
Find  .
.
Let 
Find 
Tap to reveal answer

This is a graph of  . We know that
. We know that  is undefined; therefore, there is no value for
is undefined; therefore, there is no value for  . But as we take a look at the graph, we can see that as
. But as we take a look at the graph, we can see that as  approaches 0 from the left,
approaches 0 from the left,  approaches negative infinity.
approaches negative infinity.
This can be illustrated by thinking of small negative numbers.


NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.
 is actually infinity, not negative infinity.
is actually infinity, not negative infinity.

This is a graph of 




This can be illustrated by thinking of small negative numbers.
NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.

← Didn't Know|Knew It →
The speed of a car traveling on the highway is given by the following function of time:

What can you say about the car's speed after a long time (that is, as  approaches infinity)?
approaches infinity)?
The speed of a car traveling on the highway is given by the following function of time:
What can you say about the car's speed after a long time (that is, as 
Tap to reveal answer
The function given is a polynomial with a term  , such that
, such that  is greater than 1.
is greater than 1.
Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as  approaches infinity.
approaches infinity.
This tells us that the given function is not a very realistic description of a car's speed for large  !
!
The function given is a polynomial with a term 

Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as 
This tells us that the given function is not a very realistic description of a car's speed for large 
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Calculate  .
.
Calculate 
Tap to reveal answer
This can be rewritten as follows:


![= $\lim_{x\rightarrow \infty }$\left [\left ( $x^{2}$-1 \right ) \cdot \sin $\frac{1}{ $x^{2}$$-1} \right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99922/gif.latex)

We can substitute  , noting that as
, noting that as  ,
,  :
:
 , which is the correct choice.
, which is the correct choice.
This can be rewritten as follows:
We can substitute 



← Didn't Know|Knew It →
Let  .
.
Find  .
.
Let 
Find 
Tap to reveal answer

This is a graph of  . We know that
. We know that  is undefined; therefore, there is no value for
is undefined; therefore, there is no value for  . But as we take a look at the graph, we can see that as
. But as we take a look at the graph, we can see that as  approaches 0 from the left,
approaches 0 from the left,  approaches negative infinity.
approaches negative infinity.
This can be illustrated by thinking of small negative numbers.


NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.
 is actually infinity, not negative infinity.
is actually infinity, not negative infinity.

This is a graph of 




This can be illustrated by thinking of small negative numbers.
NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.

← Didn't Know|Knew It →