Triangles - Math
Card 0 of 464
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: _c_2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: _c_2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
Compare your answer with the correct one above
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
Compare your answer with the correct one above
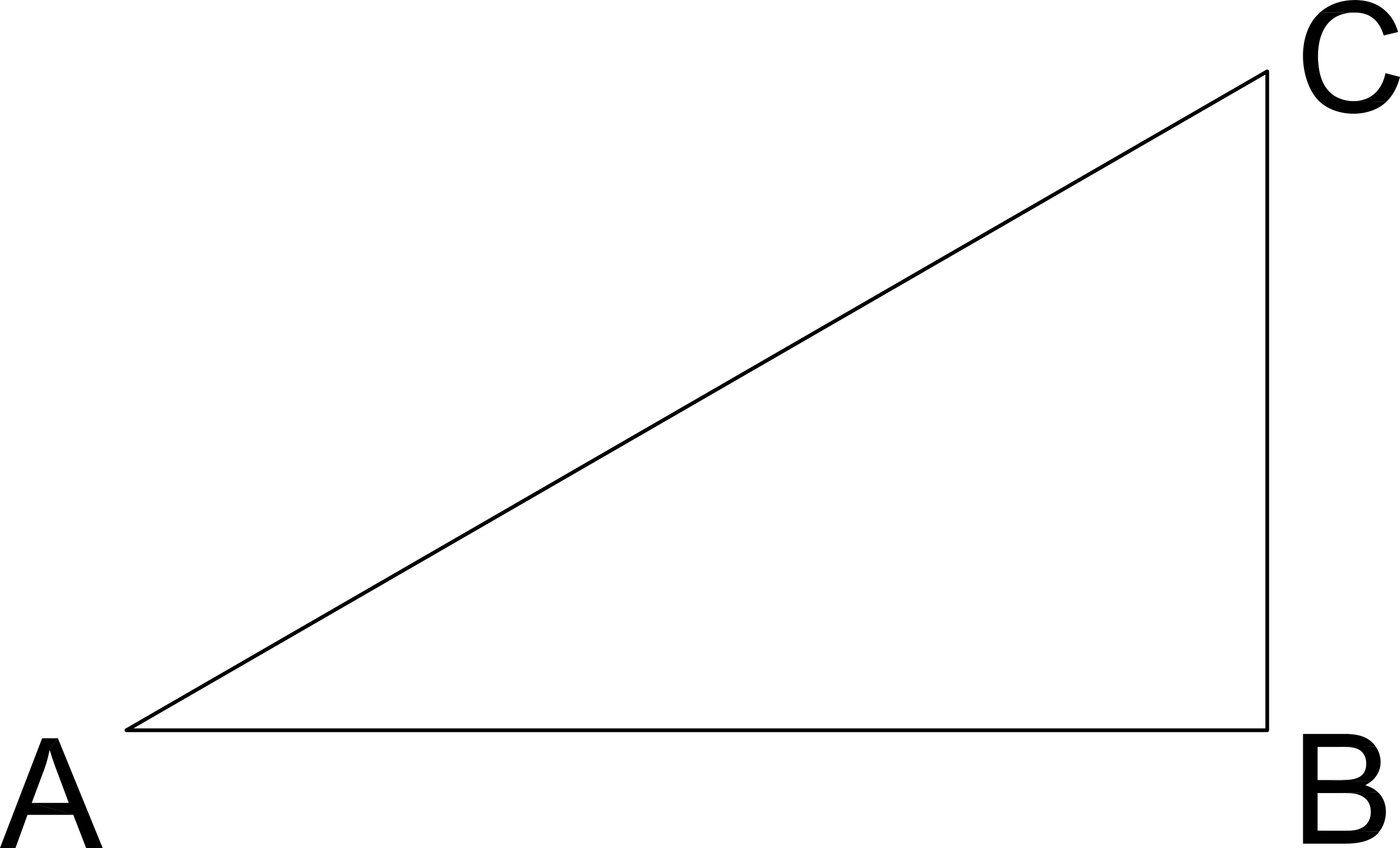
Length AB = 4
Length BC = 3
If a similar triangle has a hypotenuse length of 25, what are the lengths of its two legs?

Length AB = 4
Length BC = 3
If a similar triangle has a hypotenuse length of 25, what are the lengths of its two legs?
Similar triangles are in proportion.
Use Pythagorean Theorem to solve for AC:
Pythagorean Theorem: _AB_2 + _BC_2 = _AC_2
42 + 32 = _AC_2
16 + 9 = _AC_2
25 = _AC_2
AC = 5
If the similar triangle's hypotenuse is 25, then the proportion of the sides is AC/25 or 5/25 or 1/5.
Two legs then are 5 times longer than AB or BC:
5 * (AB) = 5 * (4) = 20
5 * (BC) = 5 * (3) = 15
Similar triangles are in proportion.
Use Pythagorean Theorem to solve for AC:
Pythagorean Theorem: _AB_2 + _BC_2 = _AC_2
42 + 32 = _AC_2
16 + 9 = _AC_2
25 = _AC_2
AC = 5
If the similar triangle's hypotenuse is 25, then the proportion of the sides is AC/25 or 5/25 or 1/5.
Two legs then are 5 times longer than AB or BC:
5 * (AB) = 5 * (4) = 20
5 * (BC) = 5 * (3) = 15
Compare your answer with the correct one above
A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?
A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?
The area of a triangle is denoted by the equation 1/2 b x h.
b stands for the length of the base, and h stands for the height.
Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.
So, 12-5 = 7 for the total perimeter of the base and height.
7 does not divide cleanly by two, but it does break down into 3 and 4,
and 1/2 (3x4) yields 6.
Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here
The area of a triangle is denoted by the equation 1/2 b x h.
b stands for the length of the base, and h stands for the height.
Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.
So, 12-5 = 7 for the total perimeter of the base and height.
7 does not divide cleanly by two, but it does break down into 3 and 4,
and 1/2 (3x4) yields 6.
Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here
Compare your answer with the correct one above
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Compare your answer with the correct one above
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = _x_2
100 + 25 = _x_2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = _x_2
100 + 25 = _x_2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
Compare your answer with the correct one above
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
Using the Pythagorean theorem, _x_2 + _y_2 = _h_2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = _h_2 . Multiplied out 25 + 25 = _h_2.
Therefore _h_2 = 50, so h = √50 = √2 * √25 or 5√2.
Using the Pythagorean theorem, _x_2 + _y_2 = _h_2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = _h_2 . Multiplied out 25 + 25 = _h_2.
Therefore _h_2 = 50, so h = √50 = √2 * √25 or 5√2.
Compare your answer with the correct one above
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
Compare your answer with the correct one above
Which of the following sets of sides cannnot belong to a right triangle?
Which of the following sets of sides cannnot belong to a right triangle?
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
Compare your answer with the correct one above
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
This can be solved with the Pythagorean Theorem.
62 + 42 = _c_2
52 = _c_2
c = √52 = 2√13
This can be solved with the Pythagorean Theorem.
62 + 42 = _c_2
52 = _c_2
c = √52 = 2√13
Compare your answer with the correct one above
Paul leaves his home and jogs 3 miles due north and 4 miles due west. If Paul could walk a straight line from his current position back to his house, how far, in miles, is Paul from home?
Paul leaves his home and jogs 3 miles due north and 4 miles due west. If Paul could walk a straight line from his current position back to his house, how far, in miles, is Paul from home?
By using the Pythagorean Theorem, we can solve for the distance “as the crow flies” from Paul to his home:
32 + 42 = _x_2
9 + 16 = _x_2
25 = _x_2
5 = x
By using the Pythagorean Theorem, we can solve for the distance “as the crow flies” from Paul to his home:
32 + 42 = _x_2
9 + 16 = _x_2
25 = _x_2
5 = x
Compare your answer with the correct one above
Which set of side lengths CANNOT correspond to a right triangle?
Which set of side lengths CANNOT correspond to a right triangle?
Because we are told this is a right triangle, we can use the Pythagorean Theorem, _a_2 + _b_2 = _c_2. You may also remember some of these as special right triangles that are good to memorize, such as 3, 4, 5.
Here, 6, 8, 11 will not be the sides to a right triangle because 62 + 82 = 102.
Because we are told this is a right triangle, we can use the Pythagorean Theorem, _a_2 + _b_2 = _c_2. You may also remember some of these as special right triangles that are good to memorize, such as 3, 4, 5.
Here, 6, 8, 11 will not be the sides to a right triangle because 62 + 82 = 102.
Compare your answer with the correct one above
Given a right triangle where the two legs have lengths of 3 and 4 respectively, what is the length of the hypotenuse?
Given a right triangle where the two legs have lengths of 3 and 4 respectively, what is the length of the hypotenuse?
The hypotenuse can be found using Pythagorean Theorem, which is a2 + b2 = c2, so we plug in a = 3 and b = 4 to get c.
c2 =25, so c = 5
The hypotenuse can be found using Pythagorean Theorem, which is a2 + b2 = c2, so we plug in a = 3 and b = 4 to get c.
c2 =25, so c = 5
Compare your answer with the correct one above
What is the hypotenuse of a right triangle with sides 5 and 8?
What is the hypotenuse of a right triangle with sides 5 and 8?
Because this is a right triangle, we can use the Pythagorean Theorem which says _a_2 + _b_2 = _c_2, or the squares of the two sides of a right triangle must equal the square of the hypotenuse. Here we have a = 5 and b = 8.
_a_2 + _b_2 = _c_2
52 + 82 = _c_2
25 + 64 = _c_2
89 = _c_2
c = √89
Because this is a right triangle, we can use the Pythagorean Theorem which says _a_2 + _b_2 = _c_2, or the squares of the two sides of a right triangle must equal the square of the hypotenuse. Here we have a = 5 and b = 8.
_a_2 + _b_2 = _c_2
52 + 82 = _c_2
25 + 64 = _c_2
89 = _c_2
c = √89
Compare your answer with the correct one above
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
Compare your answer with the correct one above
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.

To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.
Compare your answer with the correct one above
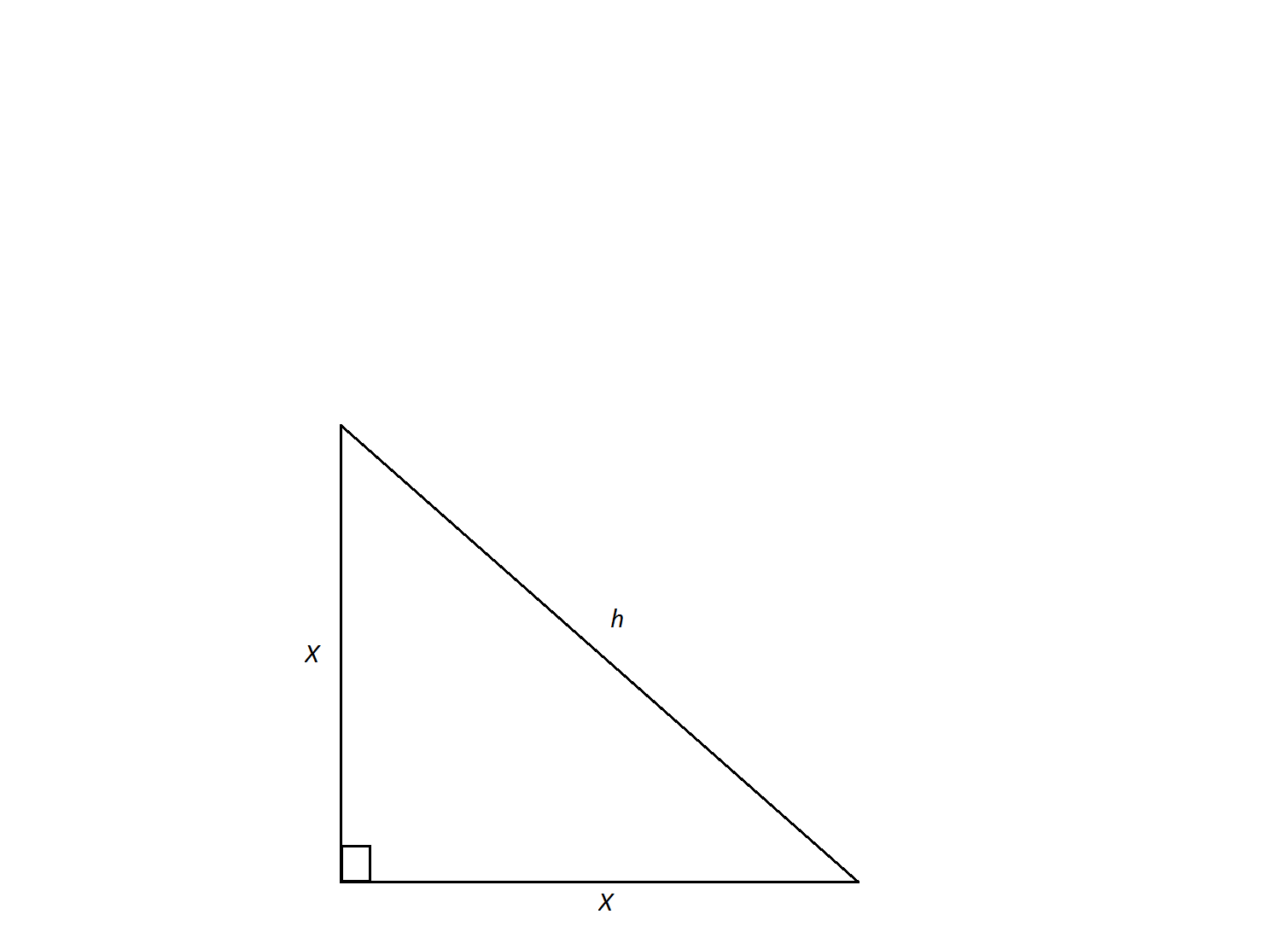
An isosceles right triangle has a hypotenuse of  . Find its area.
. Find its area.

An isosceles right triangle has a hypotenuse of 
In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as  triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.
triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.

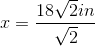

Now we can calculate the area using the formula



Now, convert to feet.

In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
Now we can calculate the area using the formula
Now, convert to feet.
Compare your answer with the correct one above
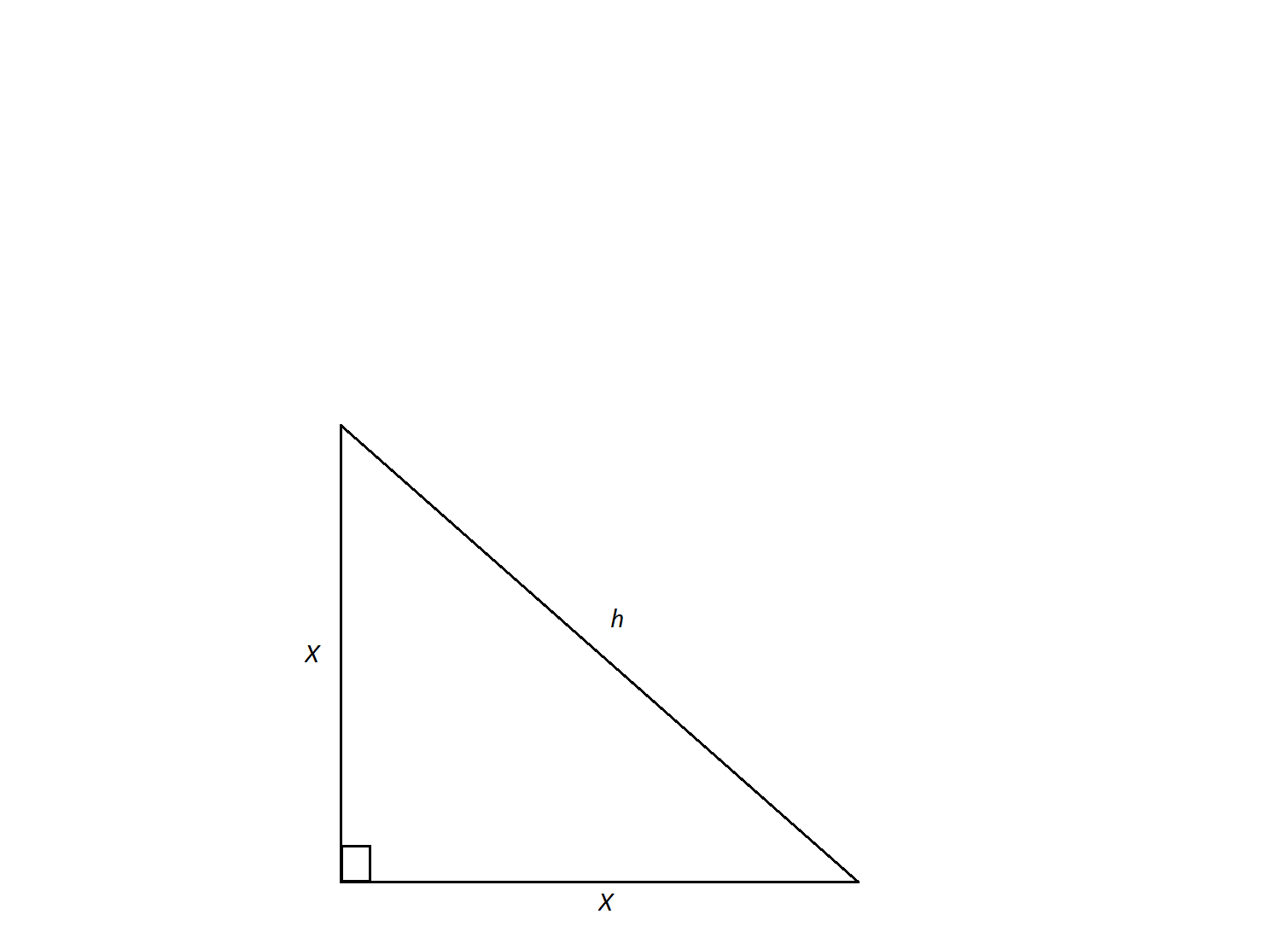
In an isosceles right triangle, two sides equal  . Find the length of side
. Find the length of side  .
.

In an isosceles right triangle, two sides equal 

This problem represents the definition of the side lengths of an isosceles right triangle. By definition the sides equal  ,
,  , and
, and  . However, if you did not remember this definition one can also find the length of the side using the Pythagorean theorem
. However, if you did not remember this definition one can also find the length of the side using the Pythagorean theorem  .
.




This problem represents the definition of the side lengths of an isosceles right triangle. By definition the sides equal 



Compare your answer with the correct one above
ABCD is a square whose side is  units. Find the length of diagonal AC.
units. Find the length of diagonal AC.
ABCD is a square whose side is 
To find the length of the diagonal, given two sides of the square, we can create two equal triangles from the square. The diagonal line splits the right angles of the square in half, creating two triangles with the angles of  ,
,  , and
, and  degrees. This type of triangle is a special right triangle, with the relationship between the side opposite the
degrees. This type of triangle is a special right triangle, with the relationship between the side opposite the  degree angles serving as x, and the side opposite the
degree angles serving as x, and the side opposite the  degree angle serving as
degree angle serving as  .
.
Appyling this, if we plug  in for
in for  we get that the side opposite the right angle (aka the diagonal) is
we get that the side opposite the right angle (aka the diagonal) is 
To find the length of the diagonal, given two sides of the square, we can create two equal triangles from the square. The diagonal line splits the right angles of the square in half, creating two triangles with the angles of 





Appyling this, if we plug 

Compare your answer with the correct one above
The area of a square is  . Find the length of the diagonal of the square.
. Find the length of the diagonal of the square.
The area of a square is 
If the area of the square is  , we know that each side of the square is
, we know that each side of the square is  , because the area of a square is
, because the area of a square is  .
.
Then, the diagonal creates two  special right triangles. Knowing that the sides =
special right triangles. Knowing that the sides =  , we can find that the hypotenuse (aka diagonal) is
, we can find that the hypotenuse (aka diagonal) is 
If the area of the square is 


Then, the diagonal creates two 

Compare your answer with the correct one above