Trigonometry - Math

Card 1 of 796

0

Didn't Know

0

Didn't Know

Knew It

0

1 of 2019 left

Question

Simplify the function below:

Tap to reveal answer

Answer

We need to use the following formulas:

a)

and

b)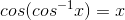

We can simplify as follows:

← Didn't Know|Knew It →

Question

What is the length of CB?

Tap to reveal answer

Answer

$\tan X= $\frac{OPPOSITE}{ADJACENT}$$

$\tan C=\frac{AB}{CB}$$

$CB= $\frac{AB}{\tan C}$$

← Didn't Know|Knew It →

Question

If $\theta$ equals and is , how long is ?

Tap to reveal answer

Answer

This problem can be easily solved using trig identities. We are given the hypotenuse and $\theta $(55^{\circ}$)$ . We can then calculate side using the $\sin$ .

$\sin=\frac{opposite}{hypotenuse}$$

Rearrange to solve for .

$\dpi{100} \rightarrow 12.3ft$

If you calculated the side to equal then you utilized the $\cos$ function rather than the $\sin$ .

← Didn't Know|Knew It →

Question

Solve for .

(Figure not drawn to scale).

Tap to reveal answer

Answer

The side-angle-side (SAS) postulate can be used to determine that the triangles are similar. Both triangles share the angle farthest to the right. In the smaller triangle, the upper edge has a length of , and in the larger triangle is has a length of . In the smaller triangle, the bottom edge has a length of , and in the larger triangle is has a length of . We can test for comparison.

$\frac{Upper\ edge_1}{Upper\ edge_2}$=\frac{Lower\ edge_1}{Lower\ edge_2}$

$\frac{8}{16}$=\frac{6}{12}$=\frac{1}{2}$

The statement is true, so the triangles must be similar.

We can use this ratio to solve for the missing side length.

$\frac{Upper\ edge_1}{Upper\ edge_2}$=\frac{Lower\ edge_1}{Lower\ edge_2}$=\frac{x}{Left\ edge_2}$

To simplify, we will only use the lower edge and left edge comparison.

$\small $\frac{6}{12}$=\frac{x}{5}$$

Cross multiply.

$\small 12x=30$

$\small x=\frac{30}{12}$=\frac{5}{2}$=2.5$

← Didn't Know|Knew It →

Question

Solve for .

(Figure not drawn to scale).

Tap to reveal answer

Answer

We can solve using the trigonometric definition of tangent.

$\small tan\Theta =\frac{opp}{adj}$$

We are given the angle and the adjacent side.

$\small $tan(22^o$)=\frac{z}{18}$$

We can find $\small $tan(22^o$)$ with a calculator.

$\small $tan(22^o$)=0.4$

$0.4=\frac{z}{18}$$

$\small 18*0.4=z$

$\small z=7.3$

← Didn't Know|Knew It →

Question

Simplify the function below:

Tap to reveal answer

Answer

We need to use the following formulas:

a)

and

b)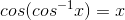

We can simplify as follows:

← Didn't Know|Knew It →

Question

Simplify the following trionometric function:

Tap to reveal answer

Answer

To solve the problem, you need to know the following information:

Replace the trigonometric functions with these values:

$$\frac{4(\frac{3}{4}$)-(1)}{($\frac{3\sqrt{2}$}{2})}$

$$\frac{2}{(\frac{3\sqrt{2}$}{2})}$

$$\frac{4}{3\sqrt{2}$} = $\frac{4\cdot \sqrt{2}$}{3$\sqrt{2}$\cdot $\sqrt{2}$} = $\frac{4\sqrt{2}$}{6} = $\frac{2\sqrt{2}$}{3}$

← Didn't Know|Knew It →

Question

Change a angle to radians.

Tap to reveal answer

Answer

In order to change an angle into radians, you must multiply the angle by $$\frac{\pi $}{180^{\circ}$$}$ .

Therefore, to solve:

← Didn't Know|Knew It →

Question

Simplify the following trigonometric function in fraction form:

Tap to reveal answer

Answer

To determine the value of the expression, you must know the following trigonometric values:

$sin $(30^{\circ}$)=\frac{1}{2}$$

Replacing these values, we get:

$$\frac{2}{4}$-$\frac{1}{2}$=\frac{1}{2}$-$\frac{1}{2}$=0$

← Didn't Know|Knew It →

Question

If $cos\ x=\frac{1}{3}$$ and $sin\ x\neq 0$ , give the value of $\frac{sin\ x+sin\ 2x}{sin\ x-sin\ 2x}$ .

Tap to reveal answer

Answer

Based on the double angle formula we have, $sin\ 2x=2(sin\ x)(cos\ x)$ .

$\frac{sin\ x+sin\ 2x}{sin\ x-sin\ 2x}$=\frac{sin\ x+2(sin\ x)(cos\ x)}{sin\ x-2(sin\ x)(cos\ x)}$

$=\frac{sinx(1+2cos\ x )}{sinx(1-2cos\ x )}$=\frac{1+2cos\ x}{1-2cos\ x}$$

$=\frac{1+2(\frac{1}{3}$)}{1-2($\frac{1}{3}$)}=\frac{\frac{3+2}{3}$}{$\frac{3-2}{3}$}=5$

← Didn't Know|Knew It →

Question

If $x=\frac{\pi}{3}$$ , give the value of $\frac{sin\ x}{sin\ x+cos\ 2x}$ .

Tap to reveal answer

Answer

$x=\frac{\pi}{3}$\Rightarrow sin\ x=sin($\frac{\pi}{3}$)=\frac{\sqrt{3}$}{2}$

Now we can write:

$x=\frac{\pi}{3}$\Rightarrow 2x=2($\frac{\pi}{3}$)=\frac{2\pi}{3}$\Rightarrow cos\ 2x=cos($\frac{2\pi}{3}$)$

$=cos(\pi-$\frac{\pi}{3}$)$

$=-cos ($\frac{\pi}{3}$)$

$=-$\frac{1}{2}$$

Now we can substitute the values:

$$\frac{sin\ x}{sin\ x+cos\ 2x}$=\frac{\frac{\sqrt{3}$}{2}}{$\frac{\sqrt{3}$}{2}-$\frac{1}{2}$}=\frac{\sqrt{3}$}{$\sqrt{3}$-1}=\frac{\sqrt{3}$}{$\sqrt{3}$-1}\times $\frac{{\sqrt{3}$+1}}{{$\sqrt{3}$+1}}=\frac{3+\sqrt{3}$}{2}$

← Didn't Know|Knew It →

Question

If $cot\ $34^{\circ}$=1.5$ , give the value of $$\frac{2sin\ $326^{\circ}$$+3sin\ $56^{\circ}$}{cos\ $304^{\circ}$}$ .

Tap to reveal answer

Answer

Now we can simplify the expression as follows:

$$\frac{2sin\ $326^{\circ}$$+3sin\ $56^{\circ}$}{cos\ $304^{\circ}$}=\frac{-2sin\ $34^{\circ}$$+3cos\ $34^{\circ}$}{sin\ $34^{\circ}$}$

$=-2+3cot\ $34^{\circ}$=-2+3\times 1.5=-2+4.5=2.5$

← Didn't Know|Knew It →

Question

If $sin\ x\times cos\ x=\frac{1}{2}$$ , what is the value of $(sin\ x+cos\ $x)^2$$ ?

Tap to reveal answer

Answer

$(sin\ x+cos\ $x)^2$$=sin^2x$$+cos^2x$+2sin\x cos\ x$

$=1+2(sin\ x)(cos\ x)=1+2($\frac{1}{2}$)=1+1=2$

← Didn't Know|Knew It →

Question

If , give the value of .

Tap to reveal answer

Answer

We know that .

← Didn't Know|Knew It →

Question

Simplify:

Tap to reveal answer

Answer

We know that .

Then we can write:

$\Rightarrow $A=\frac{(cos^2x$$-sin^2x$$)}{cos^2x$$}$+tan^2x$$

← Didn't Know|Knew It →

Question

$tan (x)sin(x) + sec(x)(cos $x)^{2}$ =$

Tap to reveal answer

Answer

$tan (x)sin(x) + sec(x)(cos $x)^{2}$ =$

$$\frac{sin (x)}{cos (x)}$* sin(x) + $\frac{1}{cos (x)}$*(cos $x)^{2}$ =$

$$\frac{(sin $x)^{2}$$ + (cos $x)^{2}$}{cos (x)} = $\frac{1}{cos (x)}$ = sec (x)$

← Didn't Know|Knew It →

Question

Simplify the following expression:

$A=cos($\frac{3\pi}{2}$+x)+sin (\pi+x)+cos($\frac{\pi}{2}$+x)+sin(\pi-x)$

Tap to reveal answer

Answer

We need to use the following identities:

$cos($\frac{3\pi}{2}$+x)=sin\ x$

$sin (\pi+x)=-sin\ x$

$cos($\frac{\pi}{2}$+x)=-sin\ x$

$sin(\pi-x)=sin\ x$

Use these to simplify the expression as follows:

$A=cos($\frac{3\pi}{2}$+x)+sin (\pi+x)+cos($\frac{\pi}{2}$+x)+sin(\pi-x)$

$\Rightarrow A=sin\ x-sin\ x-sin\ x+sin\ x = 0$

← Didn't Know|Knew It →

Question

Give the value of :

$A=\frac{2sin(\frac{\pi}{2}$)+4cos($\frac{\pi}{2}$)}{4sin($\frac{\pi}{2}$)-cos($\frac{\pi}{2}$)}$

Tap to reveal answer

Answer

$sin($\frac{\pi}{2}$)=1$

$cos($\frac{\pi}{2}$)=0$

Plug these values in:

$A=\frac{2sin(\frac{\pi}{2}$)+4cos($\frac{\pi}{2}$)}{4sin($\frac{\pi}{2}$)-cos($\frac{\pi}{2}$)}=\frac{2\times 1+4\times 0}{4\times 1-0}$=\frac{2}{4}$=\frac{1}{2}$=0.5$

← Didn't Know|Knew It →

Question

If $tan\ x = $\frac{1}{4}$$ , solve for

$D=\frac{sin\ x}{sin\ x-cos\ x}$+\frac{sin\ x+cos\ x}{cos\ x}$$

Tap to reveal answer

Answer

$tan\ x=\frac{1}{4}$\Rightarrow $\frac{sin\ x}{cos\ x}$=\frac{1}{4}$\Rightarrow cos\ x=4sin\ x$

Substitute $cos\ x=4sin \ x$ into the expression:

$D=\frac{sin\ x}{sin\ x-cos\ x}$+\frac{sin\ x+cos\ x}{cos\ x}$=\frac{sin\ x}{sin\ x-4sin\ x}$+\frac{sin\ x+4sin\ x}{4sin\ x}$$

$\Rightarrow D=\frac{sin\ x}{-3sin\ x}$+\frac{5sin\ x}{4sin\ x}$$

$\Rightarrow D=-$\frac{1}{3}$+\frac{5}{4}$=\frac{-4+15}{12}$=\frac{11}{12}$$

← Didn't Know|Knew It →

Question

If $cot\ x= 3$ , give the value of :

Tap to reveal answer

Answer

$cot\ x=3\Rightarrow $\frac{cos\ x}{sin\ x}$=3\Rightarrow cos\ x= 3sin\ x$

Now substitute $cos\ x=3sin\ x$ into the expression:

$\Rightarrow $D=\frac{9sin^2x$$}{3sin^2x$}$-$\frac{4sin\ x}{sin\ x}$$

$\Rightarrow D=\frac{9}{3}$-4=3-4=-1$

← Didn't Know|Knew It →

0

Knew It