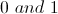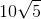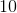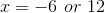The equation of a circle is , in which (h, k) is the center of the circle. To derive the center of a circle from its equation, identify the constants immediately following x and y, and flip their signs. In the given equation, x is followed by -1 and y is followed by -6, so the coordinates of the center must be (1, 6).

To convert the given equation into the format , complete the square by adding to the x-terms and to the y-terms.

The square root of 4 is 2, so the radius of the circle is 2.

To find the -intercepts (where the graph crosses the -axis), we must set . This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

and

We can then solve these two equations to obtain .

The equation of a circle is , in which (h, k) is the center of the circle and r is its radius. Because the graph of the circle is centered at (2, -3), h and k are -2 and 3. Because the radius is 4, the right side of the equation is equal to 16.

Look at the formula for the equation of a circle below.

Here is the center and is the radius. Notice that the subtraction in the center is part of the formula. Thus, looking at our equation it is clear that the center is and the radius squared is . When we square root this value we get that the radius must be .

The equation of a circle is , in which (h, k) is the center of the circle and r is its radius. Because the graph of the circle is centered at (0, 0), h and k are both 0. Because the radius is 3, the right side of the equation is equal to 9.

To convert the given equation into the format , complete the square by adding to the x-terms and to the y-terms.

The square root of 25 is 5, so the radius of the circle is 5.

The equation of a circle in standard for is:

Where the center and the radius of the cirlce is .

Dividing by 4 on both sides of the equation yields

or

an equation whose graph is a circle, centered at (2,3) with radius = .5

Rewrite the equation of the circle in standard form

as follows:

Since and , we complete the squares by adding:

The standard form of the equation sets

,

so the radius of the circle is

To find the -intercepts (where the graph crosses the -axis), we must set . This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

and

We can then solve these two equations to obtain