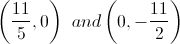Graphing Linear Functions

Help Questions

Math › Graphing Linear Functions

Questions 1 - 10

Determine where the graphs of the following equations will intersect.

Explanation

We can solve the system of equations using the substitution method.

Solve for in the second equation.

Substitute this value of into the first equation.

Now we can solve for .

$y=\frac{14}{-7}=-2$

Solve for using the first equation with this new value of .

$x=\frac{3}{3}=1$

The solution is the ordered pair .

Solve:

No solutions

Infinitely many solutions

Explanation

Use substution to solve this problem:

becomes and then is substituted into the second equation. Then solve for :

, so and to give the solution .

Determine where the graphs of the following equations will intersect.

Explanation

We can solve the system of equations using the substitution method.

Solve for in the second equation.

Substitute this value of into the first equation.

Now we can solve for .

$y=\frac{14}{-7}=-2$

Solve for using the first equation with this new value of .

$x=\frac{3}{3}=1$

The solution is the ordered pair .

Solve for the - and - intercepts:

$\left ( \frac{11}{5},0\right)\ and \left ( 0,-\frac{11}{2}\right)$

$\left ( -\frac{11}{5},0\right)\ and \left ( 0,\frac{11}{2}\right)$

$\left ( -\frac{11}{5},0\right)\ and \left ( 0,-\frac{11}{2}\right)$

$\left ( \frac{11}{5},0\right)\ and \left ( 0,\frac{11}{2}\right)$

Explanation

To solve for the -intercept, set to zero and solve for :

$x=\frac{11}{5}$

To solve for the -intercept, set to zero and solve for :

$y=-\frac{11}{2}$

What is the equation of the line passing through (-1,4) and (2,6)?

$y=\frac{2}{3}x+\frac{14}{3}$

$y=-\frac{2}{3}x+\frac{14}{3}$

$y=\frac{2}{3}x-\frac{14}{3}$

$y=3x+\frac{14}{3}$

$y=\2x+\frac{14}{3}$

Explanation

To find the equation of this line, first find the slope. Recall that slope is the change in y over the change in x: $\frac{6-4}{2+1}=\frac{2}{3}$ . Then, pick a point and use the slope to plug into the point-slope formula ( $y-y_{1}=m(x-x_{1})$ ): $y-6=\frac{2}{3}(x-2)$ . Distribute and simplify so that you solve for y: $y=\frac{2}{3}x+\frac{14}{3}$ .

Screen_shot_2014-12-24_at_2.55.25_pm

What is the equation of the above line?

Explanation

The equation of a line is with m being the slope and b being the y intercept. The y-intercept is at , so . The x-intercept is , so after plugging in the equation becomes , simplifying to .

Find the slope-intercept form of an equation of the line that has a slope of $\frac{-3}{4}$ and passes through .

$y=\frac{-3}{4}x+8$

$y=\frac{3}{4}x+8$

$y=\frac{-3}{4}x-8$

$y=\frac{4}{3}x+8$

Explanation

Since we know the slope and we know a point on the line we can use those two piece of information to find the y-intercept.

$2=\frac{-3}{4}(8)+b$

$y=\frac{-3}{4}x+8$

Determine the slope of a line that has points and .

$-\frac{2}{3}$

$-\frac{3}{2}$

$\frac{2}{3}$

$\frac{3}{2}$

Explanation

Slope is the change of a line. To find this line one can remember it as rise over run. This rise over run is really the change in the y direction over the change in the x direction.

Therefore the formula for slope is as follows.

$Slope = \frac{\Delta Y}{\Delta X}=\frac{y_2-y_1}{x_2-x_1}$

Plugging in our given points

and ,

$Slope=\frac{y2-y1}{x2-x1}=\frac{5-3}{-1-2}=\frac{2}{-3}=-\frac{2}{3}$ .

Inequality

Which of the following inequalities is graphed above?

$y \leq - \frac{3}{8} x + 3$

$y \geq - \frac{3}{8} x + 3$

$y \leq - \frac{3}{8} x +8$

$y \geq - \frac{8}{3} x - 3$

$y \geq - \frac{8}{3} x - 8$

Explanation

First, we determine the equation of the boundary line. This line includes points and , so the slope can be calculated as follows:

$m = \frac{y_{2}- y_{1}}{x_{2}- x_{1}} = \frac{3-0}{0- 8} = - \frac{3}{8}$

Since we also know the -intercept is , we can substitute $m = - \frac{3}{8}, b = 3$ in the slope-intercept form to obtain the equation of the boundary line:

$y = - \frac{3}{8} x + 3$

The boundary is included, as is indicated by the line being solid, so the equality symbol is replaced by either $\leq$ or $\geq$ . To find out which one, we can test a point in the solution set - for ease, we will choose :

$- \frac{3}{8} x + 3$

$- \frac{3}{8}\cdot 0 + 3$

0 is less than 3 so the correct symbol is $\leq$ .

The inequality is $y \leq - \frac{3}{8} x + 3$ .

Inequality

Which of the following inequalities is graphed above?

$y \leq - \frac{3}{8} x + 3$

$y \geq - \frac{3}{8} x + 3$

$y \leq - \frac{3}{8} x +8$

$y \geq - \frac{8}{3} x - 3$

$y \geq - \frac{8}{3} x - 8$

Explanation

First, we determine the equation of the boundary line. This line includes points and , so the slope can be calculated as follows:

$m = \frac{y_{2}- y_{1}}{x_{2}- x_{1}} = \frac{3-0}{0- 8} = - \frac{3}{8}$

Since we also know the -intercept is , we can substitute $m = - \frac{3}{8}, b = 3$ in the slope-intercept form to obtain the equation of the boundary line:

$y = - \frac{3}{8} x + 3$

$- \frac{3}{8} x + 3$

$- \frac{3}{8}\cdot 0 + 3$

0 is less than 3 so the correct symbol is $\leq$ .

The inequality is $y \leq - \frac{3}{8} x + 3$ .

Page 1 of 4

Return to subject

AI TutorYour personal study buddy

Questions of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games