How to find an angle in a right triangle
Help Questions
Math › How to find an angle in a right triangle
A right triangle has equal legs of 

Explanation
The equation to find the area of a triangle is:
In this problem, both the base and the height are 6in. By plugging in the numbers, we get
In the figure above, what is the positive difference, in degrees, between the measures of angle ACB and angle CBD?
10
50
40
30
20
Explanation
In the figure above, angle ADB is a right angle. Because side AC is a straight line, angle CDB must also be a right angle.
Let’s examine triangle ADB. The sum of the measures of the three angles must be 180 degrees, and we know that angle ADB must be 90 degrees, since it is a right angle. We can now set up the following equation.
x + y + 90 = 180
Subtract 90 from both sides.
x + y = 90
Next, we will look at triangle CDB. We know that angle CDB is also 90 degrees, so we will write the following equation:
y – 10 + 2_x_ – 20 + 90 = 180
y + 2_x_ + 60 = 180
Subtract 60 from both sides.
y + 2_x_ = 120
We have a system of equations consisting of x + y = 90 and y + 2_x_ = 120. We can solve this system by solving one equation in terms of x and then substituting this value into the second equation. Let’s solve for y in the equation x + y = 90.
x + y = 90
Subtract x from both sides.
y = 90 – x
Next, we can substitute 90 – x into the equation y + 2_x_ = 120.
(90 – x) + 2_x_ = 120
90 + x = 120
x = 120 – 90 = 30
x = 30
Since y = 90 – x, y = 90 – 30 = 60.
The question ultimately asks us to find the positive difference between the measures of ACB and CBD. The measure of ACB = 2_x_ – 20 = 2(30) – 20 = 40 degrees. The measure of CBD = y – 10 = 60 – 10 = 50 degrees. The positive difference between 50 degrees and 40 degrees is 10.
The answer is 10.
In right 




What is the value of 
36
30
48
32
24
Explanation
There are 180 degrees in every triangle. Since this triangle is a right triangle, one of the angles measures 90 degrees.
Therefore, 
What is the missing angle in this right triangle?
Explanation
The angles of a triangle all add up to 
This means that 
Using the fact that 90 is half of 180, we can figure out that the missing angle, x, plus 34 adds to the remaining 90, and we can just subtract

Find the measurement of 

Explanation
Recall that the angles inside of a triangle must add up to 

Thus, for the triangle in question,
Find angle C.
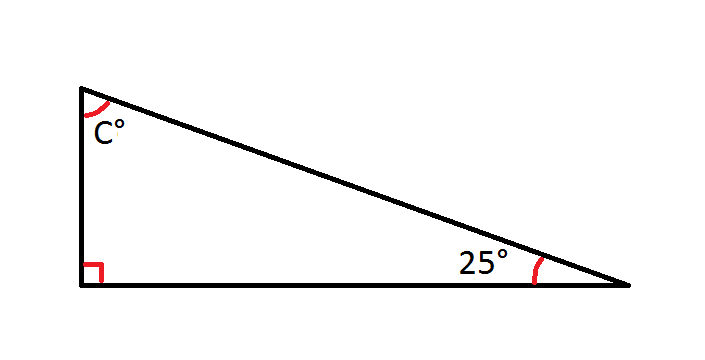
C=65
C=72
C=53
C=70
None of these
Explanation
First, know that all the angles in a triangle add up to 180 degrees.
Each triangle has 3 angles. Thus, we have the sum of three angles as shown:
where we have angles A, B, and C. In our right triangle, one angle is 25 degree and we'll call that angle A. The other known angle is 90 degrees and we'll call this angle B. Thus, we have
Simplify and solve for C.
A right triangle has another angle that is 47 degrees. What is the third angle?
Explanation
The inside of a triangle has three angles that total 180 degrees. If one is 47 and the other is the right angle (90).
Then

To find the missing angle subtract the sum above from 180.

Angle 





Explanation
The interior angles of a triangle always add up to 180 degrees. We are given angle 

Angle 
Determine the missing angle in this right triangle:
Explanation
The angles of a triangle always add to 180 degrees.
That means that in this case,

There are a few ways we can move on from here, but one is to simplify this equation:

















































