The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.

Perimeter A = 45” and perimeter B = 135”

The proportion of Perimeter A to Perimeter B is .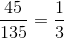

This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.

15” x 3 = 45”

10” x 3 = 30“

Angle-Angle Postulate: if two angles of one triangle are equal to two corresponding angles of another triangle, the triangles must be similar.

In this example, the triangles share one angle, which must be equal. Additionally, the triangles contain segments that are parallel to each other. When two parallel lines are crossed by another line, the corresponding angles must be equal. Each angle in one triangle is congruent with its corresponding angle in the other triangle, indicating that they are similar.

The Side-Angle-Side Postulate considers two corresponding sides and the included angle. The included angles must be congruent, and the ratios of the two corresponding sides must be equal. If both criteria are satisfied, then the triangles are similar.

In this problem, there is a shared angle, making it equal for the two triangles. Now, consider the ratios of the sides.

Simplify the fractions.

because the ratios are equal, the triangles are similar by the Side-Angle-Side postulate.

Since the two triangles are similar, each triangles three corresponding sides must have the same ratio.

The ratio of triangle one is:

If we look at the possible solutions we will see that ratio that is in triangle one is also seen in the triangle with side lengths as follows:

Side lengths of similar triangles can be expressed in proportions. Establish a proportion comparing the middle and long sides of your triangles.

10/11 = 9/x

Cross multiply and solve for x.

10x = 99

x = 9.9

The triangles are similar because of the side-angle-side postulate.

Side:

Angle:

Side:

The third side must also have a 2:3 ratio.

Cross-multiply, and solve for .

Since the two triangles are similar, each triangles three corresponding sides must have the same ratio.

The ratio of the triangle is:

Applying this ratio we are able to find the lengths of a similar triangle.

Since the two triangles are similar, each triangles three corresponding sides must have the same ratio.

The ratio of the triangle is:

Applying this ratio we are able to find the lengths of a similar triangle.

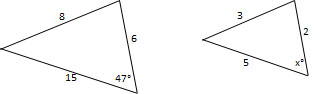
The triangles are not similar, as proven by the side-side-side postulate.

The third side does not follow the same ratio of the other two, thus the triangles are not similar.

Because the triangles are similar, a ratio can be set up between the triangles' longest sides and shortest sides as such: 14/3 = x/1. Solving for x, we obtain that the shortest side of the triangle is 14/3 units long.