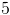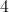How to find the area of a right triangle

Help Questions

Math › How to find the area of a right triangle

Questions 1 - 10

Rt_triangle_letters

If $c=90^\circ$ , , and , what is the area of this triangle?

Explanation

The formula for area of a triangble is $A=\frac{1}{2}bh$ .

Since $c=90^\circ$ , will be the base and will be the height.

Plug in our given values to solve:

$A=\frac{1}{2}*4*3$

Find the area of a right triangle with leg lengths of and .

Explanation

Recall how to find the area of a right triangle:

$\text{Area}=\frac{1}{2}(\text{base}\times\text{height})$

Because the legs of the right triangle form a right angle, the legs are also the base and the height.

To find the area of the right triangle, just plug in the values for the lengths of the legs into the equation given above.

$\text{Area}=\frac{1}{2}(12 \times 15)$

Simplify.

$\text{Area}=\frac{1}{2}(180)$

Solve.

$\text{Area}=90$

Find the area.

$2\sqrt3$

$4\sqrt3$

Explanation

Recall how to find the area of a triangle:

$\text{Area}=\frac{\text{base}\times\text{height}}{2}$

Now, we have the height and the hypotenuse from the question. Use the Pythagorean Theorem to find the length of the base.

$\text{hypotenuse}^2=\text{base}^2+\text{height}^2$

$\text{base}^2=\text{hypotenuse}^2-\text{height}^2$

$\text{base}=\sqrt{\text{hypotenuse}^2-\text{height}^2}$

Substitute in the values of the height and hypotenuse.

$\text{base}=\sqrt{4^2-2^2}$

Simplify.

$\text{base}=\sqrt{12}$

Reduce.

$\text{base}=2\sqrt3$

Now, substitute in the values of the base and the height to find the area.

$\text{Area}=\frac{2 \times 2\sqrt3}{2}$

Solve.

$\text{Area}=2\sqrt3$

Find the area.

Explanation

Recall how to find the area of a triangle:

$\text{Area}=\frac{\text{base}\times\text{height}}{2}$

Since this is a right triangle, the base and the height are the two leg lengths given.

$\text{Area}=\frac{14\times3}{2}=21$

If the hypotenuse of a triangle is 5 meters, which of the following is the closest value to the area of the triangle?

Explanation

The answer is 12. In this circumstance, the area of the triangle cannot be smaller than its hypotenuse length, and cannot be bigger than its hypotenuse squared (that would be the area of a square).

The hypotenuse of a $30^{\circ }-60^{\circ }-90^{\circ }$ triangle measures eight inches. What is the area of this triangle (radical form, if applicable)?

$8\sqrt{3} ; \textrm{in}^{2}$

It is impossible to tell from the information given.

$8; \textrm{{in}}^{2}$

$16 ; \textrm{in}^{2}$

$8\sqrt{2} ; \textrm{in}^{2}$

Explanation

In a $30^{\circ }-60^{\circ }-90^{\circ }$ , the shorter leg is half as long as the hypotenuse, and the longer leg is $\sqrt{3}$ times the length of the shorter. Since the hypotenuse is 8, the shorter leg is 4, and the longer leg is $4\sqrt{3}$ , making the area:

$A = \frac{1}{2} bh = \frac{1}{2} \cdot 4 \cdot 4\sqrt{3} = 8\sqrt{3}$

A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?

Explanation

The area of a triangle is denoted by the equation 1/2 b x h.

b stands for the length of the base, and h stands for the height.

Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.

So, 12-5 = 7 for the total perimeter of the base and height.

7 does not divide cleanly by two, but it does break down into 3 and 4,

and 1/2 (3x4) yields 6.

Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here

Find the area.

Explanation

Recall how to find the area of a triangle:

$\text{Area}=\frac{\text{base}\times\text{height}}{2}$

Since this is a right triangle, the base and the height are the two leg lengths given.

$\text{Area}=\frac{20\times14}{2}=140$

The diameter of the circle is , find the area of the shaded region.

Explanation

To find the area of the shaded region, we will first need to find the area of the right triangle and the area of the circle.

Recall how to find the area of a circle:

$\text{Area of Circle}=\pi\times\text{radius}^2$

Now, recall how to find the length of the radius from the length of the diameter.

$\text{Radius}=\frac{\text{Diameter}}{2}$

Substitute in the given diameter to find the radius.

$\text{Radius}=\frac{1.2}{2}$

$\text{Radius}=0.6$

Now, substitute in the radius to find the area of the circle.

$\text{Area of Circle}=\pi\times 0.6^2$

$\text{Area of Circle}=0.36\pi$

Next, recall how to find the area of a right triangle.

$\text{Area of Triangle}=\frac{\text{base}\times\text{height}}{2}$

Substitute in the given base and height to find the area.

$\text{Area of Triangle}=\frac{2 \times 15}{2}$

$\text{Area of Triangle}=15$

We can now find the area of the shaded region:

$\text{Area of Shaded Region}=\text{Area of Triangle}-\text{Area of Circle}$

$\text{Area of Shaded Region}=15-0.36\pi$

Solve and round to two decimal places.

$\text{Area of Shaded Region}=13.87$

A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?

Explanation

The area of a triangle is denoted by the equation 1/2 b x h.

b stands for the length of the base, and h stands for the height.

Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.

So, 12-5 = 7 for the total perimeter of the base and height.

7 does not divide cleanly by two, but it does break down into 3 and 4,

and 1/2 (3x4) yields 6.

Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here

Page 1 of 10

Return to subject

AI TutorYour personal study buddy

Questions of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games