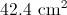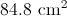How to find the area of a sector

Help Questions

Math › How to find the area of a sector

Questions 1 - 10

Find the area of the sector that has a central angle of degrees and a radius of .

Explanation

The circle in question can be drawn as shown by the figure below:

Since the area of a sector is just a fractional part of the area of a circle, we can write the following equation to find the area of a sector:

$\text{Area of Sector}=\frac{\text{Central angle}}{360}\pi r^2$ , where is the radius of the circle.

Plug in the given central angle and radius to find the area of the sector.

$\text{Area of Sector}=\frac{160}{360}\pi(12)^2=201.06$

Make sure to round to two places after the decimal.

Find the area of a sector with a central angle of degrees and a radius of .

Explanation

The circle in question could be depicted as shown in the figure.

Recall the formula for finding the area of a sector of a circle:

$\text{Area of Sector}=\frac{\text{Central Angle}}{360}\times\pi\times r^2$

Since the central angle and the radius are given in the question, plug them in to find the area of the sector.

$\text{Area of Sector}=\frac{124}{360}\times\pi\times 12^2$

Solve and round to two decimal places.

$\text{Area of Sector}=155.82$

Find the area of a sector if it has an arc length of and a radius of .

$\frac{3}{2}$

The area of the sector cannot be determined.

$\frac{5}{2}$

$\frac{7}{2}$

Explanation

The length of the arc of the sector is just a fraction of the arc of the circumference. The area of the sector will be the same fraction of the area as the length of the arc is of the circumference.

We can then write the following equation to find the area of the sector:

$\text{Area}=\frac{\text{Arc Length}}{2\pi r}\pi r^2$

The equation can be simplified to the following:

$\text{Area}=\frac{\text{Arc Length}(r)}{2}$

Plug in the given arc length and radius to find the area of the sector.

$\text{Area}=\frac{3(1)}{2}=\frac{3}{2}$

Find the area of the following sector:

$9 \pi\ m^2$

$18 \pi\ m^2$

$6 \pi\ m^2$

$3 \pi\ m^2$

$12 \pi\ m^2$

Explanation

The formula for the area of a sector is

$A = \pi r^2 (part)$ ,

where is the radius of the circle and is the fraction of the sector.

Plugging in our values, we get:

$A = \pi (6\ m)^2 (\frac{90}{360})$

$A=9 \pi\ m^2$

Find the area of the shaded region:

Screen_shot_2014-02-27_at_6.35.30_pm

$108\pi-81\sqrt{3}m^2$

$108\pi-81\sqrt{2}m^2$

$81\pi-81\sqrt{3}m^2$

$108\pi-108\sqrt{3}m^2$

$81\pi-108\sqrt{3}m^2$

Explanation

To find the area of the shaded region, you must subtract the area of the triangle from the area of the sector.

The formula for the shaded area is:

$A=A_{sector}-A_{triangle}$

$A = \pi(r^2)(part)-\frac{1}{2}(b)(h)$ ,

where is the radius of the circle, is the fraction of the sector, is the base of the triangle, and is the height of the triangle.

In order to the find the base and height of the triangle, use the formula for a triangle:

$a-a\sqrt{3}-2a$ , where is the side opposite the $\measuredangle30$ .

Plugging in our final values, we get:

$A = \pi(18m^2)(\frac{120}{360})-\frac{1}{2}(18\sqrt{3}m)(9m)$

$A = 108\pi-81\sqrt{3}m^2$

To the nearest tenth, give the area of a $60^{\circ }$ sector of a circle with diameter 18 centimeters.

$42.4 \textrm{ cm}^{2}$

$84.8 \textrm{ cm}^{2}$

$169.6 \textrm{ cm}^{2}$

$21.2 \textrm{ cm}^{2}$

$254.5 \textrm{ cm}^{2}$

Explanation

The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a $60^{\circ }$ sector of the circle is

$A = \frac{60}{360 }\cdot \pi \cdot 9^{2} =\frac{1}{6} \cdot \pi \cdot 81 \approx 42.4 \textrm{ cm}^{2}$

Find the area of a sector that has a central angle of degrees and a radius of .

Explanation

The circle in question can be drawn as shown by the figure below:

Since the area of a sector is just a fractional part of the area of a circle, we can write the following equation to find the area of a sector:

$\text{Area of Sector}=\frac{\text{Central angle}}{360}\pi r^2$ , where is the radius of the circle.

Plug in the given central angle and radius to find the area of the sector.

$\text{Area of Sector}=\frac{170}{360}\pi(3)^2=13.35$

Make sure to round to two places after the decimal.

Find the area of a sector if it has an arc length of and a radius of .

$52\pi$

$\frac{55}{2}\pi$

Explanation

The length of the arc of the sector is just a fraction of the arc of the circumference. The area of the sector will be the same fraction of the area as the length of the arc is of the circumference.

We can then write the following equation to find the area of the sector:

$\text{Area}=\frac{\text{Arc Length}}{2\pi r}\pi r^2$