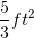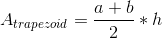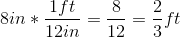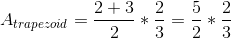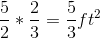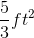How to find the area of a trapezoid

Help Questions

Math › How to find the area of a trapezoid

Questions 1 - 10

Trapezoid

In the above figure, $\overline{XY}$ is the midsegment of Trapezoid . What percent of Trapezoid has been shaded in?

$37 \frac{1}{2} %$

$33 \frac{1}{3} %$

Explanation

Midsegment $\overline{XY}$ divides Trapezoid into two trapezoids of the same height, which we will call ; the length of the midsegment is half sum of the lengths of the bases:

$XY = \frac{1}{2} (12 + 36) = \frac{1}{2} \cdot 48= 24$

The area of a trapezoid is one half multiplied by its height multiplied by the sum of the lengths of its bases. Therefore, the area of Trapezoid - the shaded trapezoid - is

$\frac{1}{2} \cdot h \cdot (TR+XY ) = \frac{1}{2} \cdot h \cdot (12+24) = \frac{1}{2} \cdot 36 \cdot h = 18 h$

The area of Trapezoid is

$\frac{1}{2} \cdot 2 h \cdot (TR+AP) = \frac{1}{2} \cdot 2 \cdot h \cdot (12+36) = \frac{1}{2} \cdot 2 \cdot 48 \cdot h = 48 h$

The percent of Trapezoid that is shaded in is

$\frac{18h}{48h} \cdot 100 % = \frac{18}{48} \cdot 100 % = 37 \frac{1}{2} %$

Trapezoid

In the above figure, $\overline{XY}$ is the midsegment of Trapezoid . Give the ratio of the area of Trapezoid to that of Trapezoid .

33 to 19

10 to 3

13 to 6

20 to 13

Explanation

Midsegment $\overline{XY}$ divides Trapezoid into two trapezoids of the same height, which we will call ; the length of the midsegment is half sum of the lengths of the bases:

$XY = \frac{1}{2} (12 + 40) = \frac{1}{2} \cdot 52 = 26$ .

The area of a trapezoid is one half multiplied by its height multiplied by the sum of the lengths of its bases. Therefore, the area of Trapezoid is

$\frac{1}{2} \cdot h \cdot (TR+XY ) = \frac{1}{2} \cdot h \cdot (12+26 ) = \frac{1}{2} \cdot 38 \cdot h = 19 h$

The area of Trapezoid is

$\frac{1}{2} \cdot h \cdot (XY +AP) = \frac{1}{2} \cdot h \cdot ( 26+40 ) = \frac{1}{2} \cdot 66 \cdot h = 33 h$

The ratio of the areas is

$\frac{33 h}{19h} = \frac{33}{19}$ , or 33 to 19.

Trapezoid

In the above figure, $\overline{XY}$ is the midsegment of Trapezoid .

Which is the greater quantity?

(a) Three times the area of Trapezoid

(b) Twice the area of Trapezoid

(b) is the greater quantity

(a) is the greater quantity

(a) and (b) are equal

It is impossible to determine which is greater from the information given

Explanation

Midsegment $\overline{XY}$ divides Trapezoid into two trapezoids of the same height, which we will call ; the length of the midsegment is half sum of the lengths of the bases:

$XY = \frac{1}{2} (12 + 36) = \frac{1}{2} \cdot 48= 24$

The area of a trapezoid is one half multiplied by its height multiplied by the sum of the lengths of its bases. Therefore, the area of Trapezoid is

$\frac{1}{2} \cdot h \cdot (TR+XY ) = \frac{1}{2} \cdot h \cdot (12+24) = \frac{1}{2} \cdot 36 \cdot h = 18 h$ .

Three times this is

$3 \cdot 18h = 54 h$ .

The area of Trapezoid is, similarly,

$\frac{1}{2} \cdot h \cdot (XY +AP ) = \frac{1}{2} \cdot h \cdot (24+36 ) = \frac{1}{2} \cdot 60 \cdot h = 30 h$

Twice this is

$2 \cdot 30 h = 60 h$ .

That makes (b) the greater quantity.

Find the area of the figure.

Explanation

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{6^2+12^2}=\sqrt{180}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(10+\sqrt{180})(4)=20+2\sqrt{180}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(6)(12)=36$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=20+2\sqrt{180}+36=82.83$

Make sure to round to places after the decimal.

Which of the following shapes is a trapezoid?

Shapes

Explanation

A trapezoid is a four-sided shape with straight sides that has a pair of opposite parallel sides. The other sides may or may not be parallel. A square and a rectangle are both considered trapezoids.

A right triangle and rectangle are placed adjacent to one another such that the composite figure formed by the triangle and rectangle is a trapezoid.

Find the area of the trapezoid given that the base of the triangle is 7 ft and the hypotenuse of the triangle is 25ft. The base of the rectangle is 9 feet.

$300ft^{2}$

$2880 ft^{2}$

$312.5 ft^{2}$

$144ft^{2}$

Explanation

$First\ we\ can\ find\ the\ height\ of\ the\ right\ triangle\ and\ assume\ that\ this\ is\ also\ the\ height\ of\ the\ rectangle\ and\ the\ trapezoid.$

$The\ height\ of\ the\ right\ triangle\ is\ obtained\ by\ using\ the\ Pythagorean\ theorem.$

$7^{2}+h^{2}=25^{2}$

$49+h^{2}=625$

$h^{2}=576$

$We\ know\ the\ top\ of\ the\ trapezoid\ is\ the\ same\ as\ the\ base\ of\ the\ rectangle\ which\ is\ 9\ cm.$

$We\ know\ that\ the\ base\ of\ the\ trapezoid\ is\ the\ sum\ of\ the\ base\ of\ the\ triangle\ and\ the\ base\ of\ the\ rectangle: 9+7=16$

$Now\ we\ have\ all\ parts\ needed\ to\ plug\ into\ the\ formula\ for\ the\ area\ of\ a\ trapezoid: A=\frac{b_{1}+b^{_{2}}}{2}*h$

$A=\frac{9+16}{2}*24=300cm^{2}$

Which is the greater quantity?

(a) The area of a trapezoid with bases 75 centimeters and 85 centimeters and height one meter.

(b) The area of a parallelogram with base 8 decimeters and height one meter.

(a) and (b) are equal.

(a) is greater.

(b) is greater.

It is impossible to tell from the information given.

Explanation

The easiet way to compare is to convert each measure to centimeters and calculate the areas in square centimeters. Both figures have height one meter, or 100 centimeters.

(a) Substitute into the formula for area:

$A = \frac{1}{2} (B + b) h$

$A = \frac{1}{2} \cdot (85 + 75 ) \cdot 100$

$A = \frac{1}{2} \cdot 160 \cdot 100$ '

square centimeters

(b) 8 decimeters is equal to 80 centimeters, so multiply this base by a height of 100 centimeters:

$A = bh = 80 \cdot 100 = 8,000$ square centimeters

The figures have the same area.

You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the depth is 8 inches, what is the area of the base of your new bookshelf?

$\frac{5}{3}ft^2$

Cannot be determined from the information provided.

$\frac{5}{2}ft^2$

$\frac{3}{5}ft^2$

Explanation

To find the area of a trapezoid, we need to use the following formula:

$A_{trapezoid}=\frac{a+b}{2}*h$

Where a and b are the lengths of the bases, and h is the perpendicular distance from one base to another.

We are given a and b, and then h will be the same as our depth. The tricky part is realizing that our depth is in inches, while our base lengths are in feet. We need to convert 8 inches to feet:

$8in*\frac{1ft}{12in}=\frac{8}{12}=\frac{2}{3}ft$