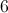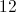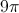How to find the length of a radius

Help Questions

Math › How to find the length of a radius

Questions 1 - 10

In a large field, a circle with an area of 144_π_ square meters is drawn out. Starting at the center of the circle, a groundskeeper mows in a straight line to the circle's edge. He then turns and mows ¼ of the way around the circle before turning again and mowing another straight line back to the center. What is the length, in meters, of the path the groundskeeper mowed?

24_π_

12 + 6_π_

12 + 36_π_

24 + 6_π_

24 + 36_π_

Explanation

Circles have an area of πr_2, where r is the radius. If this circle has an area of 144_π, then you can solve for the radius:

πr_2 = 144_π

r 2 = 144

r =12

When the groundskeeper goes from the center of the circle to the edge, he's creating a radius, which is 12 meters.

When he travels ¼ of the way around the circle, he's traveling ¼ of the circle's circumference. A circumference is 2_πr_. For this circle, that's 24_π_ meters. One-fourth of that is 6_π_ meters.

Finally, when he goes back to the center, he's creating another radius, which is 12 meters.

In all, that's 12 meters + 6_π_ meters + 12 meters, for a total of 24 + 6_π_ meters.

If the circumference of a circle is $36\pi$ , what is the radius?

$9\pi$

Explanation

The formula for circumference is $C=2\pi r$ .

Plug in our given information.

$C=2\pi r$

$36\pi=2\pi r$

Divide both sides by $2\pi$ .

$\frac{36\pi}{2\pi}=\frac{2\pi}{2\pi} r$

Find the radius of a circle with area $169\pi$ .

Explanation

Since the formula for the area of a triangle is

$A=\pi r^2$

plug in the given area and isolate for . This yields 13.

The area of Circle B is four times that of Circle A. The area of Circle C is four times that of Circle B. Which is the greater quantity?

(a) Twice the radius of Circle B

(b) The sum of the radius of Circle A and the radius of Circle C

(b) is greater.

(a) is greater.

(a) and (b) are equal.

It cannot be determined from the information given.

Explanation

Let be the radius of Circle A. Then its area is $\pi r^{2}$ .

The area of Circle B is $4\pi r^{2} =2^{2}\pi r^{2} = \pi (2r)^{2}$ , so the radius of Circle B is twice that of Circle A; by a similar argument, the radius of Circle C is twice that of Circle B, or .

(a) Twice the radius of circle B is .

(b) The sum of the radii of Circles A and B is .

This makes (b) greater.

What is the radius of a circle with a circumference of $20\pi$ ?

$20\pi$

$10\pi$

Explanation

To find the radius of a circle given the circumference we must first know the equation for the circumference of a circle which is

Then we plug in the circumference into the equation yielding

$20\pi=2r\pi$

We then divide each side by $2\pi$ giving us

The answer is .

Two concentric circles have circumferences of 4π and 10π. What is the difference of the radii of the two circles?

Explanation

The circumference of any circle is 2πr, where r is the radius.

Therefore:

The radius of the smaller circle with a circumference of 4π is 2 (from 2πr = 4π).

The radius of the larger circle with a circumference of 10π is 5 (from 2πr = 10π).

The difference of the two radii is 5-2 = 3.

A circle has an area of 36π inches. What is the radius of the circle, in inches?

Explanation

We know that the formula for the area of a circle is π_r_2. Therefore, we must set 36π equal to this formula to solve for the radius of the circle.

36π = π_r_2

36 = _r_2

6 = r

A circle has an area of 36π inches. What is the radius of the circle, in inches?

Explanation

We know that the formula for the area of a circle is π_r_2. Therefore, we must set 36π equal to this formula to solve for the radius of the circle.

36π = π_r_2

36 = _r_2

6 = r

If the diameter of a circle is equal to $5x^{2}+4x-2$ , then what is the value of the radius?

$2.5x^{2}+2x-1$

$2.5x^{2}+2x+1$

$2(x^{2}+x)-1$

Explanation

Given that the radius is equal to half the diameter, the value of the radius would be equal to $5x^{2}+4x-2$ divided by 2. This gives us:

$\frac{5x^{2}+4x-2}{2}$

$2.5x^{2}+2x-1$

The area of a circle is $81x^{2}$ . Give its radius in terms of .

(Assume is positive.)

$\frac{9x}{\sqrt{\pi}}$

$\frac{9x}{\pi}$

$\frac{81x^{2}}{\pi}$

$\frac{81x^{2}}{2\pi}$

$9 \pi x$

Explanation

The relation between the area of a circle and its radius is given by the formula

$A = \pi r^{2}$

Since

$A= 81x^{2}$ :

$81x^{2} = \pi r^{2}$

We solve for :

$\pi r^{2} = 81x^{2}$

$\frac{\pi r^{2} }{\pi}= \frac{81x^{2}}{\pi}$

$r^{2} = \frac{81x^{2}}{\pi}$

$\sqrt{r^{2} }= \sqrt{\frac{81x^{2}}{\pi}}$

Since is positive, as is :

$r =\frac{ \sqrt{81} \cdot \sqrt{x^{2}}}{\sqrt{\pi}} = \frac{9x}{\sqrt{\pi}}$

Page 1 of 6

Return to subject

AI TutorYour personal study buddy

Questions of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games