How to find the length of the side of a rectangle

Help Questions

Math › How to find the length of the side of a rectangle

Questions 1 - 10

Parallelogram

Note: Figure NOT drawn to scale

The above figure shows Rhombus .

Which is the greater quantity?

(a)

(b)

(a) and (b) are equal

It is impossible to determine which is greater from the information given

(b) is the greater quantity

(a) is the greater quantity

Explanation

The opposite sides of a parallelogram - a rhombus included - are congruent, so

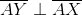
Also, Quadrilateral form a rectangle; since $\overline{AX} || \overline{CY}$ and $\overline{AY} \perp \overline{CY}$ , it follows that $\overline{AY} \perp \overline{AX}$ , and, similarly, $\overline{XC} \perp \overline{CY}$ . Therefore, , and

The two rectangles shown below are similar. What is the length of EF?

Sat_mah_166_02

Explanation

When two polygons are similar, the lengths of their corresponding sides are proportional to each other. In this diagram, AC and EG are corresponding sides and AB and EF are corresponding sides.

To solve this question, you can therefore write a proportion:

AC/EG = AB/EF ≥ 3/6 = 5/EF

From this proportion, we know that side EF is equal to 10.

If the area of a rectangle is , and the length of the rectangle is , what is the width of the rectangle?

Explanation

Recall how to find the area of a rectangle.

$\text{Area}=\text{length}\times\text{width}$

We can divide both sides by the length to find the width.

$\text{Width}=\frac{\text{Area}}{\text{length}}$

Now, plug in the information from the question.

$\text{Width}=\frac{64}{4}=16$

If the area of a rectangle is , and the length of the rectangle is , what is the width of the rectangle?

Explanation

Recall how to find the area of a rectangle.

$\text{Area}=\text{length}\times\text{width}$

We can divide both sides by the length to find the width.

$\text{Width}=\frac{\text{Area}}{\text{length}}$

Now, plug in the information from the question.

$\text{Width}=\frac{88}{8}=11$

If the perimeter of a rectangle is and the length of the rectangle is , what is the width of the rectangle?

Explanation

Recall how to find the perimeter of a rectangle.

$\text{Perimeter}=2(\text{length}+\text{width})$

We can then manipulate this equation to find the width.

$\text{length}+\text{width}=\frac{\text{Perimeter}}{2}$

$\text{width}=\frac{\text{Perimeter}}{2}-\text{length}$

Now, plug in the information given by the question to find the width.

$\text{width}=\frac{18}{2}-3=9-3=6$

A rectangle has a width of 5 meters. Its length is 2.5 times the width. What is the length of the long side and the total area of this rectangle?

None of these.

Explanation

"2.5 times the width" is equivalent to 2.5w. The length of the long side is .

The area is

A rectangle has a perimiter of 36 inches and a length of 12 inches. What is the width of the rectangle in inches?

Explanation

To find the width, multiply the length that you have been given by 2, and subtract the result from the perimeter. You now have the total length for the remaining 2 sides. This number divided by 2 is the width.

$36-(12\cdot 2)=12$