How to find the length of the side of a right triangle
Help Questions
Math › How to find the length of the side of a right triangle
Given the right triangle above, find the value of 
Explanation
To find the length of the side x, we must use the Pythagorean Theorem

However, this time since we are given the value of the hypotenuse, we will solve for side b rather than c.
So, when we plug the given values into the formula, the equation looks like
which can be simplified to

Next, solve for b and we get a final answer of

This particular example is a Pythagorean triple, or a right triangle with 3 whole number values, so it is a good one to remember.
The legs of a right triangle are 

Explanation
Use the Pythagorean Theorem. The sum of both legs squared equals the hypotenuse squared.
Consider a triangle, 



(a) 55
(b)
(b) is the greater quantity
(a) is the greater quantity
(a) and (b) are equal
It is impossible to determine which is greater from the information given
Explanation
Suppose 
By the Converse of the Pythagorean Theorem, a triangle is right if and only if the sum of the squares of the lengths of the smallest two sides is equal to the square of the longest side. Compare the quantities 
Therefore, if




However, 


Figure NOT drawn to scale.
Refer to the above triangle. Which is the greater quantity?
(a)
(b) 108
(b) is the greater quantity
(a) and (b) are equal
(a) is the greater quantity
It is impossible to determine which is greater from the information given
Explanation
We can compare these numbers by comparing their squares.
By the Pythagorean Theorem,
Also,


Given the right triangle above, find the length of the missing side.
Explanation
To find the length of the side x, we must use the Pythagorean Theorem

However, this time since we are given the value of the hypotenuse, we will solve for side b rather than c.
So, when we plug the given values into the formula, the equation looks like
which can be simplified to

Next, solve for b and we get a final answer of

This particular example is a Pythagorean triple, or a right triangle with 3 whole number values, so it is a good one to remember.

Give the length of one leg of an isosceles right triangle whose area is the same as the right triangle in the above diagram.
Explanation
The area of a triangle is half the product of its height and its base; in a right triangle, the legs, being perpendicular, can serve as these quantites.
The triangle in the diagram has area

An isosceles right triangle has two legs of the same length, which we will call 

The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
Explanation
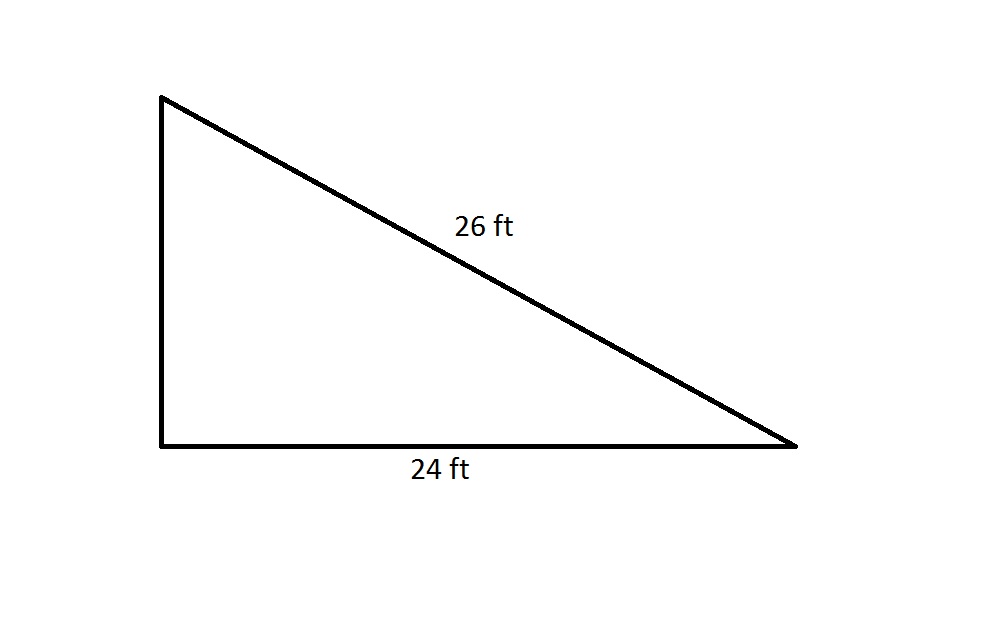
The perimeter of a regular octagon is 20% greater than that of the above right triangle. Which is the greater quantity?
(A) The length of one side of the octagon
(B) 3 yards
(A) and (B) are equal
It is impossible to determine which is greater from the information given
(A) is greater
(B) is greater
Explanation
By the Pythagorean Theorem, the shorter leg has length

The perimeter of the right triangle is therefore

The octagon has perimeter 20% greater than this, or

A regular octagon has eight sides of equal length, so each side of this octagon has length

Given a right triangle with a leg length of 2 and a hypotenuse length of √8, find the length of the other leg, x.

2
6
√8
10
4
Explanation
Using Pythagorean Theorem, we can solve for the length of leg x:
_x_2 + 22 = (√8)2 = 8
Now we solve for x:
_x_2 + 4 = 8
_x_2 = 8 – 4
_x_2 = 4
x = 2



















































 is the hypotenuse and
is the hypotenuse and  and
and  are the sides.
are the sides.