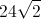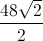Recall how to find the perimeter of a triangle:

Now, because this is a right isosceles triangle, we know the following:

From the information given in the question, we already have two of the sides needed. Now, recall the Pythagorean Theorem to find the third side of the triangle, the hypotenuse.

The Pythagorean Theorem can then be simplifed to the following equation:

Now, solve for since the question asks for the length of the hypotenuse.

Now, plug in the given value for to find the length of the hypotenuse.

Now that we have all three sides of the triangle, we can find the perimeter. Use a calculator and round to decimal places.

An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).

The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).

5 + 5 + 6 = 16

In order to solve for the perimter (the sum of all sides), all side lengths must be known.

Because it's been stated the triangle is 45/45/90, this means that it is also isosceles. Therefore, given that one of the leg lengths is 5 cm, this means that the other leg must also be 5 cm. This leaves the hypotenuse as unknown; let's label this as x.

The third side can be easily determined through the Pythagorean Theorem because it's a right triangle.

, c=x

But because the hypotenuse measures distance, x cannot be a negative number. Therefore, x=5√2.

Now, perimeter can be solved for.

When a triangle has two angles equal to , it must be a isosceles right triangle.

The pattern for the sides of a is .

Since two sides are equal to , this triangle will have sides of .

Add them all together to get .

Recall how to find the perimeter of a triangle:

Now, because this is a right isosceles triangle, we know the following:

From the information given in the question, we already have two of the sides needed. Now, recall the Pythagorean Theorem to find the third side of the triangle, the hypotenuse.

The Pythagorean Theorem can then be simplifed to the following equation:

Now, solve for since the question asks for the length of the hypotenuse.

Now, plug in the given value for to find the length of the hypotenuse.

Now that we have all three sides of the triangle, we can find the perimeter. Use a calculator and round to decimal places.

Recall how to find the perimeter of a triangle:

Now, because this is a right isosceles triangle, we know the following:

From the information given in the question, we already have two of the sides needed. Now, recall the Pythagorean Theorem to find the third side of the triangle, the hypotenuse.

The Pythagorean Theorem can then be simplifed to the following equation:

Now, solve for since the question asks for the length of the hypotenuse.

Now, plug in the given value for to find the length of the hypotenuse.

Now that we have all three sides of the triangle, we can find the perimeter. Use a calculator and round to decimal places.

Notice that the given triangle is a right isosceles triangle. The two legs with the tick marks are the same length.

The lengths of the legs in the given triangle are then .

Next, find the length of the hypotenuse by using the Pythagorean Theorem.

Plug in the value of the length of a leg to find the length of the hypotenuse.

Finally, recall how to find the perimeter of a triangle:

Plug in the values for this triangle to find its perimeter.

Make sure to round to two places after the decimal.

Notice that the given triangle is a right isosceles triangle. The two legs with the tick marks are the same length.

The lengths of the legs in the given triangle are then .

Next, find the length of the hypotenuse by using the Pythagorean Theorem.

Plug in the value of the length of a leg to find the length of the hypotenuse.

Finally, recall how to find the perimeter of a triangle:

Plug in the values for this triangle to find its perimeter.

Make sure to round to two places after the decimal.

The problem tells us the triangle is 45/45/90. The goal is to solve for the perimeter, which can be determined through , where the s's are in reference to the three sides and P stands for perimeter.

In the figure, two of the three sides are given. In order to calculate the hypotenuse, two methods are possible:

1. using the Pythagorean Theorem

2. using

After calculations, the hypotenuse is

Perimeter can be calculated out to be:

An isoceles right triangle has two congruent legs. We use the Pythagorean Theorem, which states that a2 + b2 = c2, where a and b are the legs and c is the hypotenuse.

Let = leg length.

Because this is an isosceles triangle, the two legs have the same length. Plug this and the hypotenuse length into the Pythagorean Theorem and solve for x:

Thus the perimeter is .

Plug in our value for x: