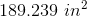How to find the surface area of a prism

Help Questions

Math › How to find the surface area of a prism

Questions 1 - 10

A small rectangular jewelry box has two square ends with areas of 36 square centimeters, and a width of 10 centimeters. What is the surface area of the outside of the jewelry box.

Explanation

To find the surface area of the rectangular box we just need to add up the areas of all six sides. We know that two of the sides are 36 square centimeters, that means we need to find the areas of the four mising sides. To find the area of the missing sides we can just multiply the side of one of the squares (6 cm) by the width of the box:

$6 \times 10 = 60 ; cm^2$

But remember we have four of these rectangular sides:

$4 \times 60 = 240 ; cm^2$

Now we just add the two square sides and four rectangular sides to find the total surface area of the jewelry box:

That is the total surface area!

Find the surface area of the regular hexagonal prism.

Explanation

In order to find the surface area, you will need to add up the areas of each face of the prism.

This hexagonal prism has two regular hexagons as its bases.

Recall how to find the area of a regular hexagon:

$\text{Area of Regular Hexagon}=\frac{3\sqrt3}{2}(\text{side}^2)$

Now, since we have two hexagons, we can multiply the area by to get the area of both bases.

$\text{Area of Bases}=3\sqrt3(\text{side})^2$

Next, this prism has rectangles that make up its sides.

Recall how to find the area of a rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.

Now, multiply the area of the rectangle by to find the total area of all of the sides of the prism.

$\text{Area of Prism Sides}=6(\text{side})(\text{height})$

Add together the area of the sides and of the bases to find the surface area of the prism.

$\text{Surface Area of Prism}=\text{Area of Bases}+\text{Area of Sides}$

$\text{Surface Area of Prism}=3\sqrt3(\text{side})^2+6(\text{side})(\text{height})$

Plug in the given values to find the surface area of the prism.

$\text{Surface Area of Prism}=3\sqrt3(8)^2+6(8)(12)=908.55$

Make sure to round to places after the decimal.

Find the surface area of the following triangular prism.

Half_box

$144 + 54\sqrt{2} m^2$

$144 + 54\sqrt{3} m^2$

$54 + 144\sqrt{2} m^2$

$54 + 144\sqrt{3} m^2$

$144 + 52\sqrt{2} m^2$

Explanation

The formula for the surface area of a triangular prism is:

$SA = 2 (base) + lateral\ area$

$SA = 2 \cdot \left(\frac{1}{2}\right)(l)(w) + (l+w+y)(h)$

Where is the length of the triangle, is the width of the triangle, is the hypotenuse of the triangle, and is the height of the prism

Use the formula for a triangle to solve for the length of the hypotenuse:

$s-s-s\sqrt{2}$

$6-6-6\sqrt{2}$

Plugging in our values, we get:

$SA = (6m)(6m) + (6m+6m+6\sqrt{2}m)(9m)$

$SA = (6m)(6m) + (12m + 6\sqrt{2}m)(9m)$

$SA = 36m^2 + 108m^2 + 54\sqrt{2}m^2 = 144 + 54\sqrt{2} m^2$

Find the surface area of the following triangular prism.

Triangular_prism

$216 + 18\sqrt{3}m^2$

$216 + 216\sqrt{3}m^2$

$18 + 18\sqrt{3}m^2$

$218 + 16\sqrt{3}m^2$

$216 + 16\sqrt{3}m^2$

Explanation

The formula for the surface area of an equilateral, triangular prism is:

$SA = 2\left(\frac{s^2\sqrt{3}}{4}\right)+(3s)(h)$

Where is the length of the triangle side and is the length of the height.

Plugging in our values, we get:

$SA = 2\left(\frac{(6m)^2\sqrt{3}}{4}\right)+(3)(6m)(12m)$

$SA = 216 + 18\sqrt{3}m^2$

Find the surface area of the regular hexagonal prism.

Explanation

In order to find the surface area, you will need to add up the areas of each face of the prism.

This hexagonal prism has two regular hexagons as its bases.

Recall how to find the area of a regular hexagon:

$\text{Area of Regular Hexagon}=\frac{3\sqrt3}{2}(\text{side}^2)$

Now, since we have two hexagons, we can multiply the area by to get the area of both bases.

$\text{Area of Bases}=3\sqrt3(\text{side})^2$

Next, this prism has rectangles that make up its sides.

Recall how to find the area of a rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.

Now, multiply the area of the rectangle by to find the total area of all of the sides of the prism.

$\text{Area of Prism Sides}=6(\text{side})(\text{height})$

Add together the area of the sides and of the bases to find the surface area of the prism.

$\text{Surface Area of Prism}=\text{Area of Bases}+\text{Area of Sides}$

$\text{Surface Area of Prism}=3\sqrt3(\text{side})^2+6(\text{side})(\text{height})$

Plug in the given values to find the surface area of the prism.

$\text{Surface Area of Prism}=3\sqrt3(18)^2+6(18)(24)=4275.55$

Make sure to round to places after the decimal.

Find the surface area of the regular hexagonal prism.

Explanation

In order to find the surface area, you will need to add up the areas of each face of the prism.

This hexagonal prism has two regular hexagons as its bases.

Recall how to find the area of a regular hexagon:

$\text{Area of Regular Hexagon}=\frac{3\sqrt3}{2}(\text{side}^2)$

Now, since we have two hexagons, we can multiply the area by to get the area of both bases.

$\text{Area of Bases}=3\sqrt3(\text{side})^2$

Next, this prism has rectangles that make up its sides.

Recall how to find the area of a rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.

Now, multiply the area of the rectangle by to find the total area of all of the sides of the prism.

$\text{Area of Prism Sides}=6(\text{side})(\text{height})$

Add together the area of the sides and of the bases to find the surface area of the prism.

$\text{Surface Area of Prism}=\text{Area of Bases}+\text{Area of Sides}$

$\text{Surface Area of Prism}=3\sqrt3(\text{side})^2+6(\text{side})(\text{height})$

Plug in the given values to find the surface area of the prism.

$\text{Surface Area of Prism}=3\sqrt3(12)^2+6(12)(15)=1828.25$

Make sure to round to places after the decimal.

Find the surface area of the rectangular prism:

The_surface_area_of_a_prism

Explanation

The_surface_area_of_a_prism

To find the surface area of a prism, the problem can be approached in one of two ways.

1. Through an equation that uses lateral area
2. Through finding the area of each side and taking the sum of all the faces

Using the second method, it's helpful to realize rectangular prisms contain faces. With that, it's helpful to understand that there are pairs of sides. That is, there are two faces with the same dimensions. Therefore, we really only have three sides for which we need to calculate areas:

Faces 1 & 2:

$15\cdot8=120$

Faces 3 & 4:

$6\cdot8=48$

Faces 5 & 6:

$15\cdot6=90$

Now, we can add up the areas of all six sides:

The surface area is .

David wants to paint the walls in his bedroom. The floor is covered by a $10\ ft \times 16\ ft$ carpet. The ceiling is $8\ ft$ tall. He selects a paint that will cover $75\ ft^2$ per quart and $300\ ft^2$ per gallon. How much paint should he buy?

1 gallon and 2 quarts

3 quarts

2 gallons and 1 quart

1 gallon

1 gallon and 1 quart

Explanation

Find the surface area of the walls: SAwalls = 2lh + 2wh, where the height is 8 ft, the width is 10 ft, and the length is 16 ft.

This gives a total surface area of 416 ft2. One gallon covers 300 ft2, and each quart covers 75 ft2, so we need 1 gallon and 2 quarts of paint to cover the walls.

Find the surface area of the regular hexagonal prism.

Explanation

In order to find the surface area, you will need to add up the areas of each face of the prism.

This hexagonal prism has two regular hexagons as its bases.

Recall how to find the area of a regular hexagon:

$\text{Area of Regular Hexagon}=\frac{3\sqrt3}{2}(\text{side}^2)$

Now, since we have two hexagons, we can multiply the area by to get the area of both bases.

$\text{Area of Bases}=3\sqrt3(\text{side})^2$

Next, this prism has rectangles that make up its sides.

Recall how to find the area of a rectangle:

$\text{Area of Rectangle}=\text{length}\times\text{width}$

In this prism, the length is also the side of the hexagon, and the width of the rectangle is the height of the prism.

Now, multiply the area of the rectangle by to find the total area of all of the sides of the prism.

$\text{Area of Prism Sides}=6(\text{side})(\text{height})$

Add together the area of the sides and of the bases to find the surface area of the prism.

$\text{Surface Area of Prism}=\text{Area of Bases}+\text{Area of Sides}$

$\text{Surface Area of Prism}=3\sqrt3(\text{side})^2+6(\text{side})(\text{height})$

Plug in the given values to find the surface area of the prism.

$\text{Surface Area of Prism}=3\sqrt3(13)^2+6(13)(17)=2204.15$

Make sure to round to places after the decimal.

What is the surface area of an equilateral triangluar prism with edges of 6 in and a height of 12 in?

Let $\sqrt{3}=1.732$ and $\sqrt{2}=1.414$ .

$247.176\ in^{2}$

$268.732\ in^{2}$

$216.414\ in^{2}$

$189.239\ in^{2}$

$165.135\ in^{2}$

Explanation

The surface area of the prism can be broken into three rectangular sides and two equilateral triangular bases.

The area of the sides is given by: $A=lw=12\cdot 6=72\ in^{2}$ , so for all three sides we get $\dpi{100} 216\ in^{2}$ .

The equilateral triangle is also an equiangular triangle by definition, so the base has congruent sides of 6 in and three angles of 60 degrees. We use a special right traingle to figure out the height of the triangle: 30 - 60 - 90. The height is the side opposite the 60 degree angle, so it becomes $3\sqrt{3}$ or 5.196.

The area for a triangle is given by $A=\frac{1}{2}bh$ and since we need two of them we get $A=bh=6\cdot 3\sqrt{3}=31.176\ in^{2}$ .

Therefore the total surface area is $216\ in^{2}+31.176\ in^{2}=247.176\ in^{2}$ .

Page 1 of 3

Return to subject

AI TutorYour personal study buddy

Questions of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games