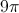How to find the volume of a cylinder

Help Questions

Math › How to find the volume of a cylinder

Questions 1 - 10

What is the volume of a cylinder with a radius of 6 meters and a height of 11 meters? Use 3.14 for $\pi$ .

Note: The formula for the volume of a cylinder is:

$V=\pi r^2h$

Explanation

To calculate the volume, you must plug into the formula given in the problem. When you plug in, it should look like this: . Multiply all of these out and you get . The units are cubed because volume is always cubed.

What is the volume of a hollow cylinder with an outer diameter of , an inner diameter of and a length of ?

$270\pi ; in^{3}$

$300\pi ; in^{3}$

$288\pi ; in^{3}$

$250\pi ; in^{3}$

$320\pi ; in^{3}$

Explanation

The general formula for the volume of a hollow cylinder is given by $V=\pi (r_{o}^{2}-r_{i}^{2})l$ where $r_{o}$ is the outer radius, $r_{i}$ is the inner radius, and is the length.

The question gives diameters and we need to convert them to radii by cutting the diameters in half. Remember, . So the equation to solve becomes:

$V=\pi (4^{2}-1^{2})18$ or $V=270\pi; in^{3}$

What is the surface area of a cylinder with a radius of 2 cm and a height of 10 cm?

40π cm2

32π cm2

56π cm2

48π cm2

36π cm2

Explanation

SAcylinder = 2πrh + 2πr2 = 2π(2)(10) + 2π(2)2 = 40π + 8π = 48π cm2

What is the surface area of a cylinder with a base diameter of and a height of ?

$36\pi in^{2}$

$14\pi in^{2}$

$66\pi in^{2}$

$48\pi in^{2}$

None of the answers

Explanation

Area of a circle $A=\pi r^{2}=\pi(\frac{d}{2})^{2}=\pi(\frac{6}{2})^{2}=\pi(3)^{2}=9\pi in^{2}$

Circumference of a circle $C=\pi d=6\pi in^{2}$

Surface area of a cylinder $SA=2A+hC=2(9\pi)+8(6\pi)=18\pi+48\pi=66\pi in^{2}$

The volume of a cylinder is $81\pi$ . If the radius of the cylinder is , what is the surface area of the cylinder?

$72\pi$

$9\pi$

$27\pi$

$3\pi$

$81\pi$

Explanation

The volume of a cylinder is equal to:

$V=\pi r^2h$

Use this formula and the given radius to solve for the height.

$81\pi=\pi(3)^2h$

$81\pi=9\pi(h)$

Now that we know the height, we can solve for the surface area. The surface area of a cylinder is equal to the area of the two bases plus the area of the outer surface. The outer surface can be "unwrapped" to form a rectangle with a height equal to the cylinder height and a base equal to the circumference of the cylinder base. Add the areas of the two bases and this rectangle to find the total area.

$A=2A_{base}+A_{rec}$

$A=2\pi r^2+(2\pi r)(h)$

Use the radius and height to solve.

$A=2\pi (3)^2+2\pi (3)(9)$

$A=18\pi+54\pi$

$A=72\pi$

What is the volume of a cylinder with a radius of and a height of ?

$135\pi$

$9\pi$

$9\pi+15$

$96\pi$

$54\pi$

Explanation

When thinking of a 3D figure, think of it as a stack of something. In this case, a cylinder is a stack of a circles.

The volume will be the area of that base circle times the height of the cylinder. Mathematically that would be $V=(\pi r^2)*h$ .

Plug in our given values and solve.

$V=(\pi r^2)*h$

$V=(\pi (3)^2)*15$

$V=9\pi*15$

$V=135\pi$

Calculate the volume of a cylinder with a height of six, and a base with a radius of three.

$54\pi$

$18\pi$

Explanation

The volume of a cylinder is give by the equation $\small V=\pi r^2h$ .

In this example, $\small h=6$ and $\small r=3$ .

$V=\pi(3)^2(6)$

$V=\pi(9)(6)=54\pi$

This figure is a right cylinder with radius of 2 m and a height of 10 m.

What is the volume of the right cylinder (m3)?

Explanation

The formula for the volume of a right cylinder is $\pi r^{2}h$ where is the radius and is the height. Thus for this problem

$\pi\cdot2^{2}\cdot10=125.71$

Cylinder_with_a_sphere

A sphere with a radius of is circumscribed in a cylinder. What is the cylinder's volume?

$50.27cm^{3}$

$\dpi{100} 27.50cm^{3}$

$\dpi{100} 28.27cm^{3}$

Not enough information to solve

$27.28cm^{3}$

Explanation

In order to solve this problem, one key fact needs to be understood. A sphere will take up exactly $\frac{2}{3}$ of the volume of a cylinder in which it is circumscribed. Therefore, if we find the volume of the sphere we can then solve for the volume of the cylinder.

First, we need to find the volume of the sphere.

$\dpi{100} V=\frac{4}{3}\pi (2cm)^{3}$

$\dpi{100} \dpi{100} V_{sphere}=10\frac{2}{3}\pi cm^{3}$

This equals $\frac{2}{3}$ of the volume of the cylinder. Therefore,

$\dpi{100} V_{cylinder}=\frac{3}{2}(10\frac{2}{3}\pi cm^{3})$

$\rightarrow 50.27cm^{3}$

What is the volume of a cylinder with a radius of 2 and a length that is three times as long as its diameter?

$48\pi$

$12\pi$

$16\pi$

Explanation

The volume of a cylinder is the base multiplied by the height or length. The base is the area of a circle, which is $\pi r^{2}$ . Here, the radius is 2. The diameter is 4. Three times the diameter is 12. The height or length is 12. So, the answer is $48\pi$ .

Page 1 of 7

Return to subject

AI TutorYour personal study buddy

Questions of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games